北师大版七年级数学上册 第二章 有理数及其运算 复习课件(共27张PPT)
文档属性
| 名称 | 北师大版七年级数学上册 第二章 有理数及其运算 复习课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 436.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 11:49:25 | ||
图片预览







文档简介
(共27张PPT)
第二章 有理数及其运算 复习课件
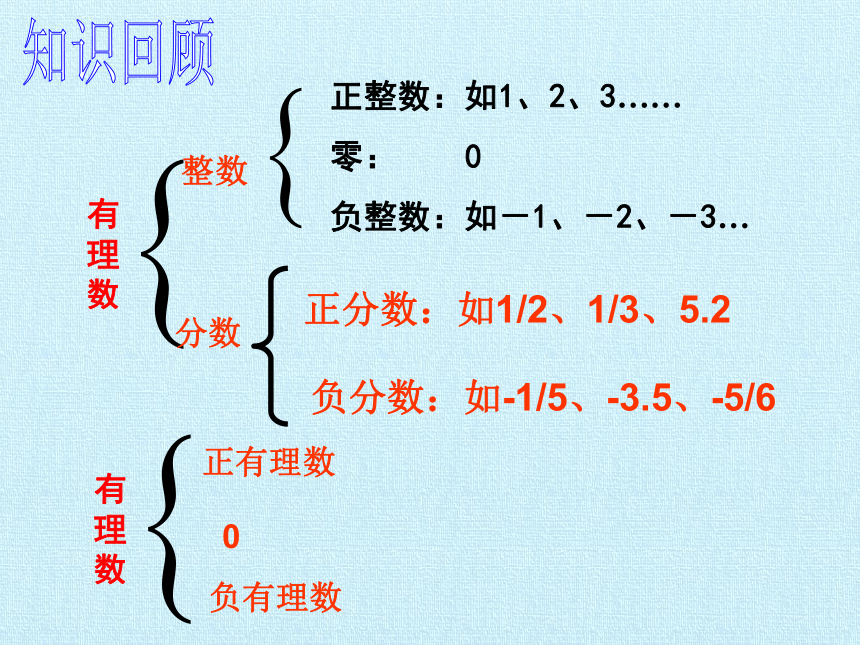
有理数
整数
分数
有理数
正有理数
负有理数
0
正整数:如1、2、3……
零: 0
负整数:如-1、-2、-3…
正分数:如1/2、1/3、5.2
负分数:如-1/5、-3.5、-5/6
知识回顾
例:把各数分别表示在数轴上,并填在相应的集合里。
8、-1/8、-1、-8、-(-1/8)、0。
整数集合( )
分数集合( )
正数集合( )
负数集合 ( )
正整数集合( )
有理数集合 ( )
知识回顾
知识回顾
1、数轴:原点、正方向、单位长度(三要素)。
任何一个有理数都可以用数轴上的点来表示。
A点表示______,B点表示______,C点表示______,D点表示______,E点表示______。
总结:一条正确的数轴,必须要有______,______,______。
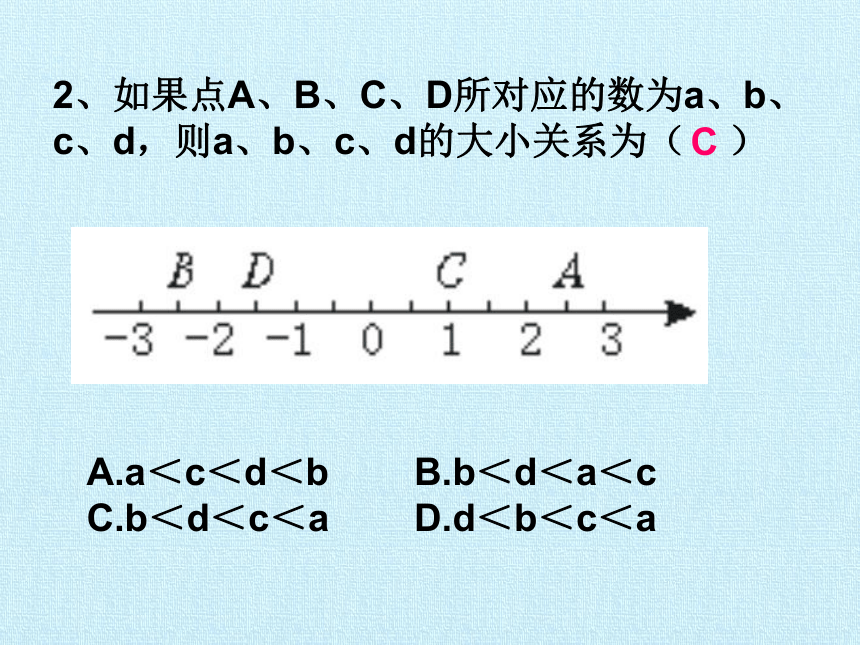
2、如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系为( )
A.a<c<d<b B.b<d<a<c
C.b<d<c<a D.d<b<c<a
C
知识回顾
数轴:在数轴上一个数所对应的点与原点
的距离叫做该数的绝对值。
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
如:+2的绝对值是2,记作|+2|=2;
-2的绝对值是2,记作|-2|=2。
___的倒数是它本身,________的绝对值是它本身。
3.a+b=0,则a与b_______。
4.最大的负整数与绝对值最小的数的和是____。
5.若b<0且a=|b|,则a与b的关系是_________。
1.
填空题
±1
正数和零
互为相反数
-1
互为相反数
6.如果|a|>a,那么a是_____。
7.某人向东走了4千米记作+4千米,那么-2千米表示_________?
8.如果-|a|=|a|,那么a_____。
a<0
向西走了2千米
=0
9.如果▲表示最小的正整数,●表示最大的负整数,■表示绝对值最小的有理数,那么(▲+●)×■= 。
0
10.已知|a|+|b|+|c|=0,
则a=____,b=_____,c=____。
11.在数轴上与表示-1的点相距4个单位长度的点表示的数是_____。
12.在数轴上距离原点为2的点所对应的数为_______,它们互为____。
则x=__,y=___。
13.若
0
0
0
-6 -5 -4 -3 -2 -1 0 1 2 3 4
-5,3
-2,-2
相反数
2
3
14.右图是正方体的侧面展开图,请你在其余三个空格内填入适当的数,使折成正方体后相对的面上的两个数互为相反数。
0.5
-1
-3
1
-0.5
3
1.若|x|-|y|=0,则( )
A.x=y B.x=-y
C.x=y=0 D.x=y或x=-y
2.有理数a,b在数轴上对应位置如图所示,
则a+b的值为( )
A.大于0 B.小于0
C.等于0 D.大于a
选择题
D
B
3.|x|=1,则x与-3的差为( )
A.4 B.-2
C.4或2 D.2
C
|x|=1,∴x=±1
1-(-3)=4
-1-(-3)
=-1+=2
∴选C。
4.下列说法中,正确的是( )
A. 一个有理数的绝对值不小于它自身
B. 若两个有理数的绝对值相等,则这两个数相等
C. 若两个有理数的绝对值相等则这两个数互为相反数
D. -a的绝对值等于a
A
5.下列说法中,正确的是( )
A.0是最小的有理数
B.0是最小整数
C.0的倒数和相反数都是0
D.0是最小的非负数
6.下列结论正确的是( )
A.若|x|=|y|,则x=-y
B.若x=-y,则|x|=|y|
C.若|a|<|b|,则a<b
D.若a<b,则|a|<|b|
D
B
7.校、家、书店依次坐落在一条南北走向的大街上,学校在家的南边20米,书店在家北边100米,张明同学从家里出发,向北走了50米,接着又向北走了-70米,此时张明的位置在( )
A.在家 B.在学校
C.在书店 D.不在上述地方
-80 -60 -40 -20 0 20 40 60 80 100 120 140
学校
家
书店
B
8.下列计算正确的是( )
D
9.写出大于-4.1且小于2.5的所有整数,数并把它们在数轴上表示出来。
大于-4、1且小于2.5的所有整数为-4、-3、-2、-1、0、1、2。
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
a
n
底数
指数
运算的结果叫做幂
读做a的n次方,看作是a的n次方结果时,也可读做a的n次幂。
填空:
(1)(-2)10的底数是___,指数是____,读作_________。
(2)(-3)12表示______个_______相乘,读作_________。
(3)(-1/3)8的指数是________,底数______读作_______。
(4)3.65的指数是_________,底数是________,读作_______。
(5)xm表示____个_____相乘,指数是______,底数是_______,读作_________。
熟悉乘方
在有理数运算中,有时利用运算律可以简化计算。哪位同学举例说明有理数的运算律有哪些?
如:13+(-12)+17+(-18)
=13+17+(-12)+(-18)
=30+(-30)
=0
加法交换律,
结合律
乘法交换律,结合律
有理数的加法运算律和乘法运算律与小学学过的运算律相同。当符号确定之后,就归结为小学学过的加减运算和乘除运算。
有理数的运算律为:加法的交换律、加法结合律、乘法的交换律、乘法结合律,乘法对加法的分配律。
计算:(1)11+(-22)-3×(-11)
解:(1)11+(-22)-3×(-11)
=11+(-22) –( - 33 )
=11+(-22)+33
=22
先乘除,后加减
注意符号!
解.
2.观察下列等式:9-1=8,16-4=12,25-9=16,36-16=20,…,
设n为正整数(n≥1),用关于n的等式表示上述等式的规律是_________________________。
1.观察下列等式:
71=7,72=49,73=343,74=2401,…,由此可判断7100的个位数字是 。
1
(n+2)2-n2=4 (n+1)
3.已知一张纸对折一次,然后沿折线撕开,再把所得的两张纸再对折撕开,再把所得的四张纸重叠对折撕开,由此进行五次,把每次所得纸的张数填入下表:
撕纸次数 1 2 3 4 5 …… n
纸的张数 ……
2
4
8
16
32
例:下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数)。
(1)如果现在的北京时间是7:00,那么现在的纽约时间是多少?
(2)小明现在想给远在巴黎的姑妈打电话,你认为合适吗?
城 市 时差/时
纽 约 -13
巴 黎 -7
东 京 +1
芝加哥 -14
解:(1)-13+7=-6 (2)-7+7=0
答:(1)昨天18点 (2)不适合
谢 谢
第二章 有理数及其运算 复习课件
有理数
整数
分数
有理数
正有理数
负有理数
0
正整数:如1、2、3……
零: 0
负整数:如-1、-2、-3…
正分数:如1/2、1/3、5.2
负分数:如-1/5、-3.5、-5/6
知识回顾
例:把各数分别表示在数轴上,并填在相应的集合里。
8、-1/8、-1、-8、-(-1/8)、0。
整数集合( )
分数集合( )
正数集合( )
负数集合 ( )
正整数集合( )
有理数集合 ( )
知识回顾
知识回顾
1、数轴:原点、正方向、单位长度(三要素)。
任何一个有理数都可以用数轴上的点来表示。
A点表示______,B点表示______,C点表示______,D点表示______,E点表示______。
总结:一条正确的数轴,必须要有______,______,______。
2、如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系为( )
A.a<c<d<b B.b<d<a<c
C.b<d<c<a D.d<b<c<a
C
知识回顾
数轴:在数轴上一个数所对应的点与原点
的距离叫做该数的绝对值。
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
如:+2的绝对值是2,记作|+2|=2;
-2的绝对值是2,记作|-2|=2。
___的倒数是它本身,________的绝对值是它本身。
3.a+b=0,则a与b_______。
4.最大的负整数与绝对值最小的数的和是____。
5.若b<0且a=|b|,则a与b的关系是_________。
1.
填空题
±1
正数和零
互为相反数
-1
互为相反数
6.如果|a|>a,那么a是_____。
7.某人向东走了4千米记作+4千米,那么-2千米表示_________?
8.如果-|a|=|a|,那么a_____。
a<0
向西走了2千米
=0
9.如果▲表示最小的正整数,●表示最大的负整数,■表示绝对值最小的有理数,那么(▲+●)×■= 。
0
10.已知|a|+|b|+|c|=0,
则a=____,b=_____,c=____。
11.在数轴上与表示-1的点相距4个单位长度的点表示的数是_____。
12.在数轴上距离原点为2的点所对应的数为_______,它们互为____。
则x=__,y=___。
13.若
0
0
0
-6 -5 -4 -3 -2 -1 0 1 2 3 4
-5,3
-2,-2
相反数
2
3
14.右图是正方体的侧面展开图,请你在其余三个空格内填入适当的数,使折成正方体后相对的面上的两个数互为相反数。
0.5
-1
-3
1
-0.5
3
1.若|x|-|y|=0,则( )
A.x=y B.x=-y
C.x=y=0 D.x=y或x=-y
2.有理数a,b在数轴上对应位置如图所示,
则a+b的值为( )
A.大于0 B.小于0
C.等于0 D.大于a
选择题
D
B
3.|x|=1,则x与-3的差为( )
A.4 B.-2
C.4或2 D.2
C
|x|=1,∴x=±1
1-(-3)=4
-1-(-3)
=-1+=2
∴选C。
4.下列说法中,正确的是( )
A. 一个有理数的绝对值不小于它自身
B. 若两个有理数的绝对值相等,则这两个数相等
C. 若两个有理数的绝对值相等则这两个数互为相反数
D. -a的绝对值等于a
A
5.下列说法中,正确的是( )
A.0是最小的有理数
B.0是最小整数
C.0的倒数和相反数都是0
D.0是最小的非负数
6.下列结论正确的是( )
A.若|x|=|y|,则x=-y
B.若x=-y,则|x|=|y|
C.若|a|<|b|,则a<b
D.若a<b,则|a|<|b|
D
B
7.校、家、书店依次坐落在一条南北走向的大街上,学校在家的南边20米,书店在家北边100米,张明同学从家里出发,向北走了50米,接着又向北走了-70米,此时张明的位置在( )
A.在家 B.在学校
C.在书店 D.不在上述地方
-80 -60 -40 -20 0 20 40 60 80 100 120 140
学校
家
书店
B
8.下列计算正确的是( )
D
9.写出大于-4.1且小于2.5的所有整数,数并把它们在数轴上表示出来。
大于-4、1且小于2.5的所有整数为-4、-3、-2、-1、0、1、2。
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
a
n
底数
指数
运算的结果叫做幂
读做a的n次方,看作是a的n次方结果时,也可读做a的n次幂。
填空:
(1)(-2)10的底数是___,指数是____,读作_________。
(2)(-3)12表示______个_______相乘,读作_________。
(3)(-1/3)8的指数是________,底数______读作_______。
(4)3.65的指数是_________,底数是________,读作_______。
(5)xm表示____个_____相乘,指数是______,底数是_______,读作_________。
熟悉乘方
在有理数运算中,有时利用运算律可以简化计算。哪位同学举例说明有理数的运算律有哪些?
如:13+(-12)+17+(-18)
=13+17+(-12)+(-18)
=30+(-30)
=0
加法交换律,
结合律
乘法交换律,结合律
有理数的加法运算律和乘法运算律与小学学过的运算律相同。当符号确定之后,就归结为小学学过的加减运算和乘除运算。
有理数的运算律为:加法的交换律、加法结合律、乘法的交换律、乘法结合律,乘法对加法的分配律。
计算:(1)11+(-22)-3×(-11)
解:(1)11+(-22)-3×(-11)
=11+(-22) –( - 33 )
=11+(-22)+33
=22
先乘除,后加减
注意符号!
解.
2.观察下列等式:9-1=8,16-4=12,25-9=16,36-16=20,…,
设n为正整数(n≥1),用关于n的等式表示上述等式的规律是_________________________。
1.观察下列等式:
71=7,72=49,73=343,74=2401,…,由此可判断7100的个位数字是 。
1
(n+2)2-n2=4 (n+1)
3.已知一张纸对折一次,然后沿折线撕开,再把所得的两张纸再对折撕开,再把所得的四张纸重叠对折撕开,由此进行五次,把每次所得纸的张数填入下表:
撕纸次数 1 2 3 4 5 …… n
纸的张数 ……
2
4
8
16
32
例:下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数)。
(1)如果现在的北京时间是7:00,那么现在的纽约时间是多少?
(2)小明现在想给远在巴黎的姑妈打电话,你认为合适吗?
城 市 时差/时
纽 约 -13
巴 黎 -7
东 京 +1
芝加哥 -14
解:(1)-13+7=-6 (2)-7+7=0
答:(1)昨天18点 (2)不适合
谢 谢
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
