苏科版九年级数学上册第2章对称图形-圆小结与思考20课件(共41张PPT)
文档属性
| 名称 | 苏科版九年级数学上册第2章对称图形-圆小结与思考20课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 13:45:50 | ||
图片预览




文档简介
(共41张PPT)
小结与思考
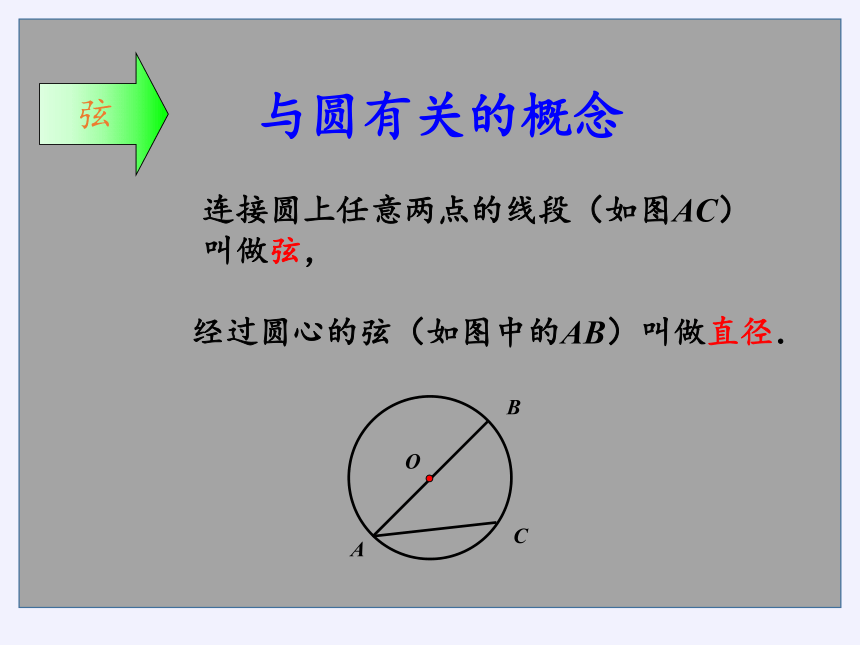
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
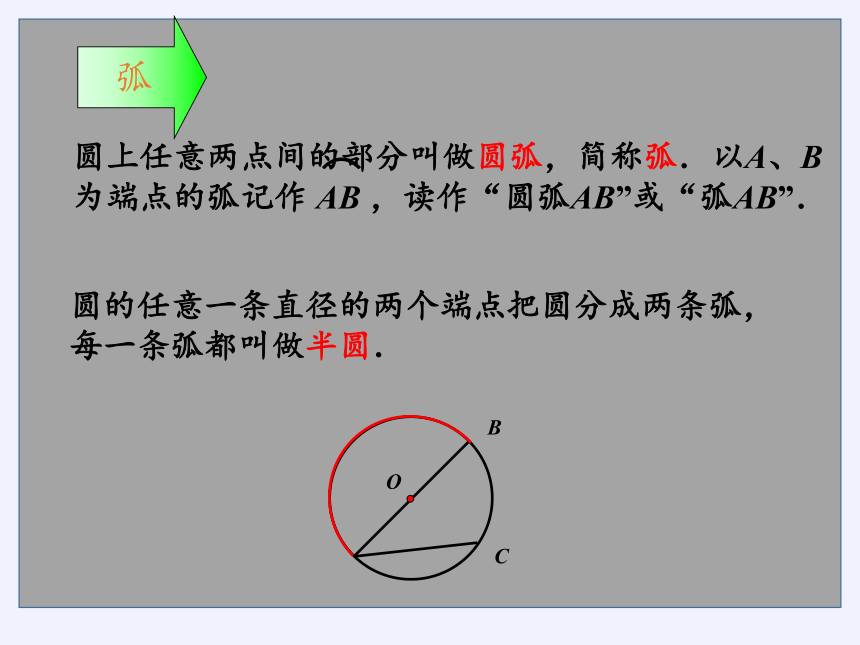
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
B
弧
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
·
C
O
A
B
劣弧与优弧
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ABC)
弓形:由弦及其所对的弧组成的图形叫弓形。
等圆:能够重合的两个圆叫做等圆,易知同圆或等圆的半径相等。
同心圆:圆心相同,半径不相等的两个圆叫做同心圆
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
等弧应同时满足两个条件:1)两弧的长度相等,
2)两弧的度数相等。
1、直径是弦,而弦不一定是直径;
2、半圆是弧,而弧不一定是半圆;
3、两条等弧的度数相等,长度也相等,
反之,度数相等或长度相等的两条弧不一定是等弧。
注意:
想一想
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)等弧就是拉直以后长度相等的弧
随堂练习
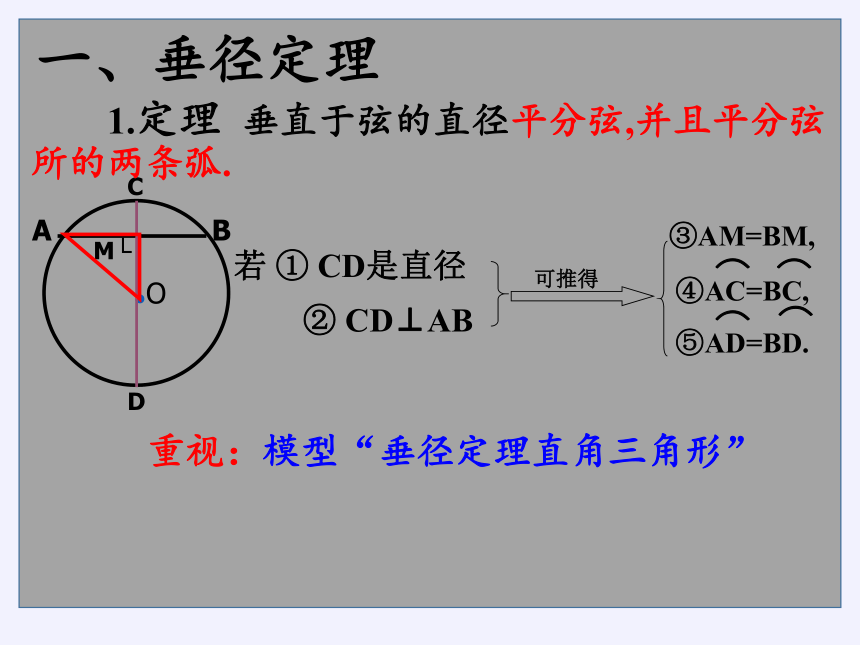
一、垂径定理
●O
A
B
C
D
M└
重视:模型“垂径定理直角三角形”
③AM=BM,
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
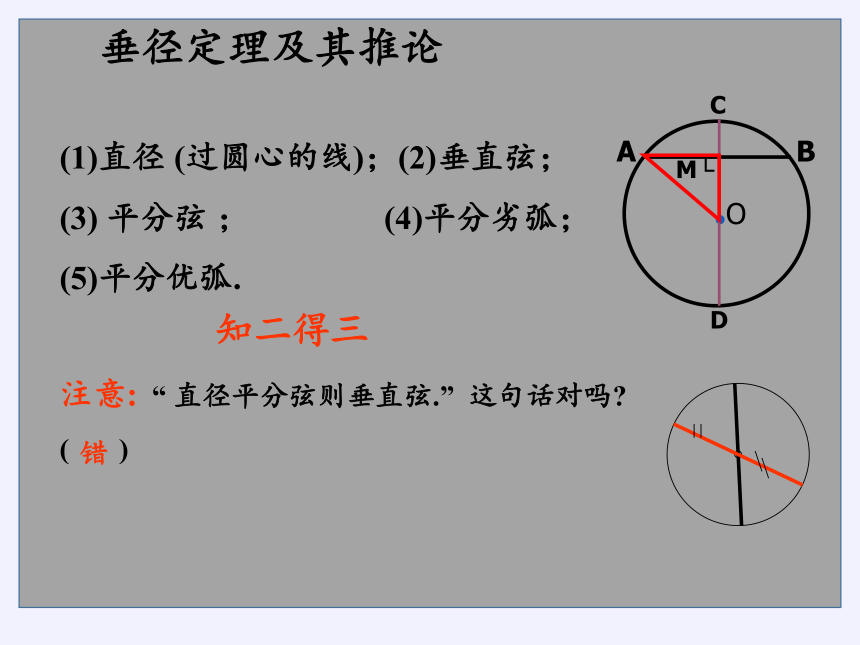
直径 (过圆心的线);(2)垂直弦;
(3) 平分弦 ; (4)平分劣弧;
(5)平分优弧.
知二得三
注意: “ 直径平分弦则垂直弦.” 这句话对吗
( )
错
●O
A
B
C
D
M└
垂径定理及其推论
●O
A
B
C
D
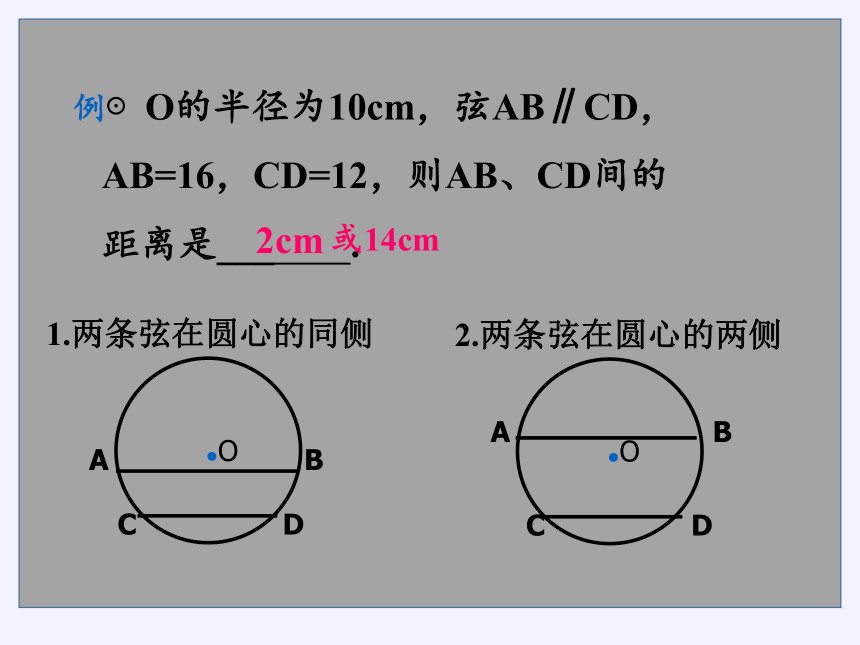
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .
2cm
或14cm
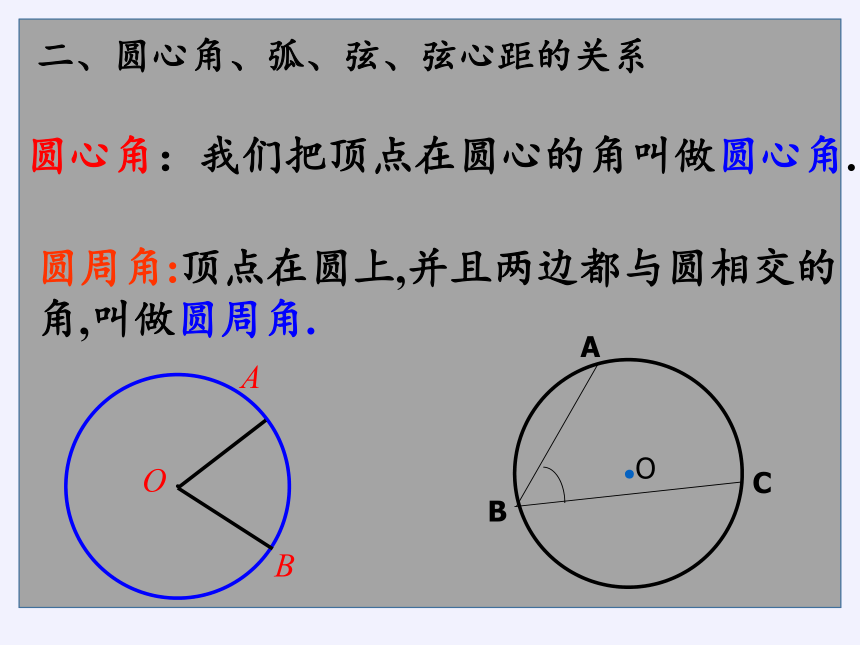
圆心角:我们把顶点在圆心的角叫做圆心角.
圆周角:顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
·
O
B
A
●O
B
A
C
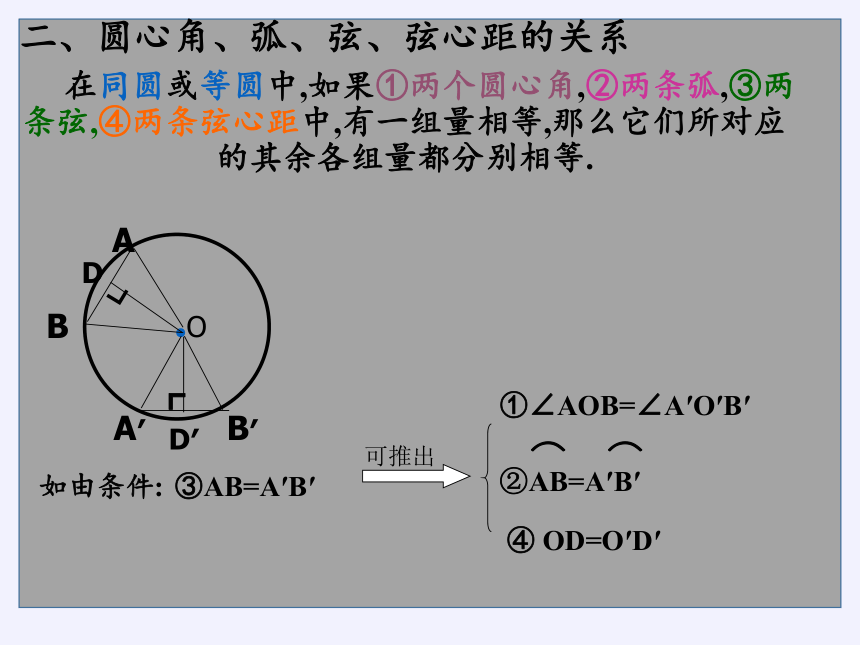
二、圆心角、弧、弦、弦心距的关系
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
二、圆心角、弧、弦、弦心距的关系
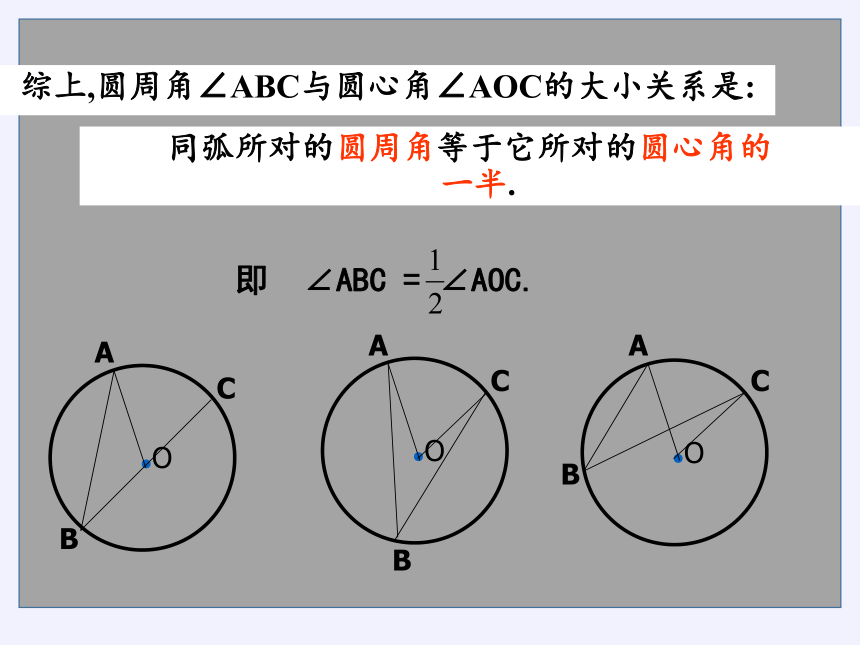
综上,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的
一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
三、圆周角定理及推论
90°的圆周角所对的弦是 .
●O
B
A
C
D
E
●O
A
B
C
定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,
都等于这弧所对的圆心角的一半.
推论:直径所对的圆周角是 .
直角
直径
判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.
(×)
(×)
(√)
随堂练习
1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、已知弧AB 、弧AC是同圆的两段弧,且弧AB等于2倍弧AC,则弦AB与CD之间的关系为( );
A.AB=2CD B.AB<2CD C.AB>2CD D.不能确定
图1
3、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
4、在△ABC中,∠A=70°,若O为△ABC的外心,∠BOC= ;若O为△ABC的内心,∠BOC= .
图2
5、两个同心圆的直径分别为5 cm和3 cm,则圆环部分的宽度为_____ cm;
6、如图1,已知⊙O,AB为直径,AB⊥CD,垂足为E,由图你还能知道哪些正确的结论 请把它们一一写出来 ;
7、为改善市区人民生活环境,市建设污水管网工程,某圆柱型水管的直径为100 cm,截面如图2,若管内污水的面宽AB=60 cm,则污水的最大深度为 cm;
图1 图2
.P
.O
r
四、点和圆的位置关系
Op<r 点p在⊙O内
Op=r 点p在⊙O上
Op>r 点p在⊙O外
.P
.O
r
.P
.O
r
练习:有两个同心圆,半径分别为R和r,
P是圆环内一点,
则OP的取值范围是_____.
r经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
不在同一直线上的三个点确定一个圆
圆内接四边形的性质:
(1)对角互补;
(2)任意一个外角都等于它的内对角
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=_____ cm.
随堂练习
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4
B、1∶3∶2∶4
C、4∶2∶3∶1
D、4∶2∶1∶3
1、直线和圆相交
五.直线与圆的位置关系
d r;
d r;
2、直线和圆相切
3、直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
切线的判定定理
定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
●O
A
如图
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.
(1)定义
(2)圆心到直线的距离d=圆的半径r
(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定方法
切线的判定定理的两种应用
1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.
切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径
C
D
●O
A
∴CD⊥OA.
做一做:1、两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC=_____ cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是( ).
①与圆有公共点的直线是该圆的切线 ; ②垂直于圆的半径的直线是该圆的切线 ; ③到圆心的距离等于半径的直线是该圆的切线 ;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①② B.②③ C.③④ D.①④
一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则
它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之
比 .
×
√
6.5cm
2cm
2:1
随堂练习
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
C
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
30cm
随堂练习
A
B
C
O
六.三角形的外接圆和内切圆:
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
实质 性质
三角形的外心
三角形的内心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
三角形的外心是否一定在三角形的内部?
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
A
B
P
●O
┗
┏
1
2
A
B
C
●
┗
┏
┓
O
D
E
F
┗
●
A
B
C
●
O
●
┗
┓
O
D
E
F
┗
切线长定理及其推论:
直角三角形的内切圆半径与三边关系.
三角形的内切圆半径与圆面积.
∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2
1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30或150度
随堂练习
2:已知ABC三点在圆O上,连接ABCO,如果∠ AOC=140 °,求∠ B的度数.
3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.
D
解:在优弧AC上定一点D,连结AD、
CD.
∵ ∠ AOC=140 °
∴ ∠ D=70 °
∴ ∠ B=180 ° -70 ° =110 °
2或4cm
4.怎样要将一个如图所示的破镜重圆?
A
B
C
P
5、 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能帮老师求出这面镜子的半径吗?
O
7
14
综合应用垂径定理和勾股定理可求得半径
6.如图:AB是圆O的直径,BD是圆O的弦,
BD到C,AC=AB,BD与CD的大小有什么关系?
为什么?
补充:
若∠B=70 °,则∠DOE=___.
E
40 °
7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
A
B
C
D
E
O
.
谢 谢
小结与思考
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
B
弧
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
·
C
O
A
B
劣弧与优弧
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ABC)
弓形:由弦及其所对的弧组成的图形叫弓形。
等圆:能够重合的两个圆叫做等圆,易知同圆或等圆的半径相等。
同心圆:圆心相同,半径不相等的两个圆叫做同心圆
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
等弧应同时满足两个条件:1)两弧的长度相等,
2)两弧的度数相等。
1、直径是弦,而弦不一定是直径;
2、半圆是弧,而弧不一定是半圆;
3、两条等弧的度数相等,长度也相等,
反之,度数相等或长度相等的两条弧不一定是等弧。
注意:
想一想
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)等弧就是拉直以后长度相等的弧
随堂练习
一、垂径定理
●O
A
B
C
D
M└
重视:模型“垂径定理直角三角形”
③AM=BM,
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
直径 (过圆心的线);(2)垂直弦;
(3) 平分弦 ; (4)平分劣弧;
(5)平分优弧.
知二得三
注意: “ 直径平分弦则垂直弦.” 这句话对吗
( )
错
●O
A
B
C
D
M└
垂径定理及其推论
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .
2cm
或14cm
圆心角:我们把顶点在圆心的角叫做圆心角.
圆周角:顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
·
O
B
A
●O
B
A
C
二、圆心角、弧、弦、弦心距的关系
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
二、圆心角、弧、弦、弦心距的关系
综上,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的
一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
三、圆周角定理及推论
90°的圆周角所对的弦是 .
●O
B
A
C
D
E
●O
A
B
C
定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,
都等于这弧所对的圆心角的一半.
推论:直径所对的圆周角是 .
直角
直径
判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.
(×)
(×)
(√)
随堂练习
1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、已知弧AB 、弧AC是同圆的两段弧,且弧AB等于2倍弧AC,则弦AB与CD之间的关系为( );
A.AB=2CD B.AB<2CD C.AB>2CD D.不能确定
图1
3、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
4、在△ABC中,∠A=70°,若O为△ABC的外心,∠BOC= ;若O为△ABC的内心,∠BOC= .
图2
5、两个同心圆的直径分别为5 cm和3 cm,则圆环部分的宽度为_____ cm;
6、如图1,已知⊙O,AB为直径,AB⊥CD,垂足为E,由图你还能知道哪些正确的结论 请把它们一一写出来 ;
7、为改善市区人民生活环境,市建设污水管网工程,某圆柱型水管的直径为100 cm,截面如图2,若管内污水的面宽AB=60 cm,则污水的最大深度为 cm;
图1 图2
.P
.O
r
四、点和圆的位置关系
Op<r 点p在⊙O内
Op=r 点p在⊙O上
Op>r 点p在⊙O外
.P
.O
r
.P
.O
r
练习:有两个同心圆,半径分别为R和r,
P是圆环内一点,
则OP的取值范围是_____.
r
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
不在同一直线上的三个点确定一个圆
圆内接四边形的性质:
(1)对角互补;
(2)任意一个外角都等于它的内对角
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=_____ cm.
随堂练习
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4
B、1∶3∶2∶4
C、4∶2∶3∶1
D、4∶2∶1∶3
1、直线和圆相交
五.直线与圆的位置关系
d r;
d r;
2、直线和圆相切
3、直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
切线的判定定理
定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
●O
A
如图
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.
(1)定义
(2)圆心到直线的距离d=圆的半径r
(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定方法
切线的判定定理的两种应用
1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.
切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径
C
D
●O
A
∴CD⊥OA.
做一做:1、两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC=_____ cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是( ).
①与圆有公共点的直线是该圆的切线 ; ②垂直于圆的半径的直线是该圆的切线 ; ③到圆心的距离等于半径的直线是该圆的切线 ;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①② B.②③ C.③④ D.①④
一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则
它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之
比 .
×
√
6.5cm
2cm
2:1
随堂练习
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
C
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
30cm
随堂练习
A
B
C
O
六.三角形的外接圆和内切圆:
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
实质 性质
三角形的外心
三角形的内心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
三角形的外心是否一定在三角形的内部?
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
A
B
P
●O
┗
┏
1
2
A
B
C
●
┗
┏
┓
O
D
E
F
┗
●
A
B
C
●
O
●
┗
┓
O
D
E
F
┗
切线长定理及其推论:
直角三角形的内切圆半径与三边关系.
三角形的内切圆半径与圆面积.
∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2
1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30或150度
随堂练习
2:已知ABC三点在圆O上,连接ABCO,如果∠ AOC=140 °,求∠ B的度数.
3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.
D
解:在优弧AC上定一点D,连结AD、
CD.
∵ ∠ AOC=140 °
∴ ∠ D=70 °
∴ ∠ B=180 ° -70 ° =110 °
2或4cm
4.怎样要将一个如图所示的破镜重圆?
A
B
C
P
5、 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能帮老师求出这面镜子的半径吗?
O
7
14
综合应用垂径定理和勾股定理可求得半径
6.如图:AB是圆O的直径,BD是圆O的弦,
BD到C,AC=AB,BD与CD的大小有什么关系?
为什么?
补充:
若∠B=70 °,则∠DOE=___.
E
40 °
7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
A
B
C
D
E
O
.
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
