2021-2022学年 人教版数学八年级上册13.3 等腰三角形 第5课时 含30°角的直角三角形的性质课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年 人教版数学八年级上册13.3 等腰三角形 第5课时 含30°角的直角三角形的性质课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 402.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 16:15:20 | ||
图片预览





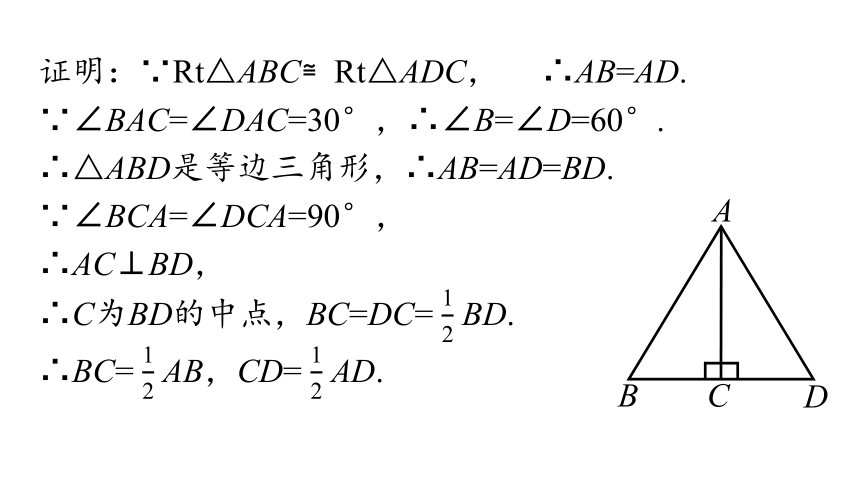



文档简介
(共21张PPT)
人教版 数学 八年级上册
第3节 等腰三角形
第5课时 含30°角的直角三角形的性质
第十三章 轴对称
等边三角形的判定方法有哪些?
1.三边相等的三角形是等边三角形;
2.三个角都相等的三角形是等边三角形;
3.有一个角是60°的等腰三角形是等边三角形.
复习旧知
用直尺量一量含有30°角的直角三角板的最短直角边(即30°角所对的直角边)与斜边的长度,你有什么发现吗?
如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与AB之间的数量吗?
A
B
C
D
导入新知
1.掌握含有30°角的直角三角形的性质和应用.
2.探索并证明含有30°角的直角三角形的性质,并用以解决实际问题.
学习目标
含30°角的直角三角形的性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图,在Rt△ABC中,∠C=90°,
∵∠A=30°,
∴BC= AB.
A
C
B
新知 含30°角的直角三角形的性质
合作探究
证明:∵Rt△ABC≌Rt△ADC, ∴AB=AD.
∵∠BAC=∠DAC=30°,∴∠B=∠D=60°.
∴△ABD是等边三角形,∴AB=AD=BD.
∵∠BCA=∠DCA=90°,
∴AC⊥BD,
∴C为BD的中点,BC=DC= BD.
∴BC= AB,CD= AD.
A
B
D
C
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
证明:在斜边AB上截取BD=BC,连接CD.
A
C
B
D
∵在Rt△ABC中,∠A=30°, ∴∠B=60°.
∵BD=BC,∠B=60° ,∴△BCD为等边三角形,
∴∠DCB=60°,CD=BC=BD.∴∠ACD=∠A=30°,
∴AD=CD.∴BC=CD=BD=AD. ∴BC= AB.
几何语言:在Rt△ABC中,
∵∠C=90°,BC= AB,∴∠A=30°.
A
C
B
D
拓展 直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
这个性质反过来说还成立吗?请试着证明你的猜想.
在Rt△ABC中,∠C=90°,∠B=2∠A,∠B,∠A各是多少度?边AB与BC之间有什么关系?
解:∵∠C=90°,∠B=2∠A.
∴∠B+∠A=180°-∠C,即3∠A=90°.
∴ ∠A=30°,∠B=60°.
∵在Rt△ABC中,∠A=30°,
∴AB=2BC.
A
C
B
典例精析
如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
A
B
C
M
N
MN//BC , CM平分∠ACB
△CMN为等腰三角形
MN平分∠AMC
∠AMN=30°,NM=MC=2
BC=2AC=6
B
课堂练习
解:∵在Rt△ABC中,CM平分∠ACB,∴∠NCM=∠BCM.
∵MN//BC,∴∠AMN=∠B,∠NMC=∠BCM.
∴△MNC为等腰三角形. ∴NM=NC.
∵MN平分∠AMC,∴∠AMN=∠CMN =∠BCM=30°.
在Rt△ANM中, ∠AMN=30°,AN=1,
∴ NM=NC=2. ∴AC=AN+NC=3.
在Rt△ABC中, ∵∠AMN=∠B=30°, ∴BC=2AC=6.
含30°角的直角三角形
性质
判定(拓展)
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
归纳新知
1.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=8.求CE的长.
课后练习
2.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°.求CD的长.
解:如图,延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°,AE=2BE.
又∵∠ADC=120°,∴∠EDC=60°.
∴∠ECD=60°.∴△DCE是等边三角形.
∴CD=CE=DE.
∵AD=4,BC=1,
∴2(1+CD)=4+CD,解得CD=2.
3.如图,在四边形ABCD中,∠B=90°,DC∥AB,AC平分∠BAD,∠DAB=30°.求证AD=2BC.
证明:如图,过点C作CE⊥AD交AD的延长线于点E.
∵DC∥AB,∠DAB=30°,
∴∠DCA=∠BAC,∠CDE=30°.
在Rt△CDE中,∠CDE=30°,∴CD=2CE.
又∵AC平分∠DAB,
∴∠DAC=∠BAC=∠DCA.∴AD=CD.∴AD=2CE.
∵CE⊥AE,CB⊥AB,AC平分∠BAD,
∴BC=CE.∴AD=2BC.
4.如图,点P是△ABC的边BC上一点,PC=2PB,∠ABC=45°,∠APC=60°.求∠ACB的度数.
解:如图,过点C作CD⊥AP于点D,连接BD.
∵∠APC=60°,∴∠PCD=30°.
∴PC=2PD.
∵PC=2PB,∴PB=PD.
∴∠PBD=∠PDB=30°.∴∠PCD=∠PBD.
∴BD=CD.∵∠ABC=45°,∴∠ABD=15°.
又∵∠BAP=∠APC-∠ABC=15°,
∴∠ABD=∠BAP.
∴AD=BD.
∴AD=CD.
∴∠DAC=∠DCA=45°.
∴∠ACB=45°+30°=75°.
再 见
人教版 数学 八年级上册
第3节 等腰三角形
第5课时 含30°角的直角三角形的性质
第十三章 轴对称
等边三角形的判定方法有哪些?
1.三边相等的三角形是等边三角形;
2.三个角都相等的三角形是等边三角形;
3.有一个角是60°的等腰三角形是等边三角形.
复习旧知
用直尺量一量含有30°角的直角三角板的最短直角边(即30°角所对的直角边)与斜边的长度,你有什么发现吗?
如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与AB之间的数量吗?
A
B
C
D
导入新知
1.掌握含有30°角的直角三角形的性质和应用.
2.探索并证明含有30°角的直角三角形的性质,并用以解决实际问题.
学习目标
含30°角的直角三角形的性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图,在Rt△ABC中,∠C=90°,
∵∠A=30°,
∴BC= AB.
A
C
B
新知 含30°角的直角三角形的性质
合作探究
证明:∵Rt△ABC≌Rt△ADC, ∴AB=AD.
∵∠BAC=∠DAC=30°,∴∠B=∠D=60°.
∴△ABD是等边三角形,∴AB=AD=BD.
∵∠BCA=∠DCA=90°,
∴AC⊥BD,
∴C为BD的中点,BC=DC= BD.
∴BC= AB,CD= AD.
A
B
D
C
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
证明:在斜边AB上截取BD=BC,连接CD.
A
C
B
D
∵在Rt△ABC中,∠A=30°, ∴∠B=60°.
∵BD=BC,∠B=60° ,∴△BCD为等边三角形,
∴∠DCB=60°,CD=BC=BD.∴∠ACD=∠A=30°,
∴AD=CD.∴BC=CD=BD=AD. ∴BC= AB.
几何语言:在Rt△ABC中,
∵∠C=90°,BC= AB,∴∠A=30°.
A
C
B
D
拓展 直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
这个性质反过来说还成立吗?请试着证明你的猜想.
在Rt△ABC中,∠C=90°,∠B=2∠A,∠B,∠A各是多少度?边AB与BC之间有什么关系?
解:∵∠C=90°,∠B=2∠A.
∴∠B+∠A=180°-∠C,即3∠A=90°.
∴ ∠A=30°,∠B=60°.
∵在Rt△ABC中,∠A=30°,
∴AB=2BC.
A
C
B
典例精析
如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
A
B
C
M
N
MN//BC , CM平分∠ACB
△CMN为等腰三角形
MN平分∠AMC
∠AMN=30°,NM=MC=2
BC=2AC=6
B
课堂练习
解:∵在Rt△ABC中,CM平分∠ACB,∴∠NCM=∠BCM.
∵MN//BC,∴∠AMN=∠B,∠NMC=∠BCM.
∴△MNC为等腰三角形. ∴NM=NC.
∵MN平分∠AMC,∴∠AMN=∠CMN =∠BCM=30°.
在Rt△ANM中, ∠AMN=30°,AN=1,
∴ NM=NC=2. ∴AC=AN+NC=3.
在Rt△ABC中, ∵∠AMN=∠B=30°, ∴BC=2AC=6.
含30°角的直角三角形
性质
判定(拓展)
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
归纳新知
1.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=8.求CE的长.
课后练习
2.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°.求CD的长.
解:如图,延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°,AE=2BE.
又∵∠ADC=120°,∴∠EDC=60°.
∴∠ECD=60°.∴△DCE是等边三角形.
∴CD=CE=DE.
∵AD=4,BC=1,
∴2(1+CD)=4+CD,解得CD=2.
3.如图,在四边形ABCD中,∠B=90°,DC∥AB,AC平分∠BAD,∠DAB=30°.求证AD=2BC.
证明:如图,过点C作CE⊥AD交AD的延长线于点E.
∵DC∥AB,∠DAB=30°,
∴∠DCA=∠BAC,∠CDE=30°.
在Rt△CDE中,∠CDE=30°,∴CD=2CE.
又∵AC平分∠DAB,
∴∠DAC=∠BAC=∠DCA.∴AD=CD.∴AD=2CE.
∵CE⊥AE,CB⊥AB,AC平分∠BAD,
∴BC=CE.∴AD=2BC.
4.如图,点P是△ABC的边BC上一点,PC=2PB,∠ABC=45°,∠APC=60°.求∠ACB的度数.
解:如图,过点C作CD⊥AP于点D,连接BD.
∵∠APC=60°,∴∠PCD=30°.
∴PC=2PD.
∵PC=2PB,∴PB=PD.
∴∠PBD=∠PDB=30°.∴∠PCD=∠PBD.
∴BD=CD.∵∠ABC=45°,∴∠ABD=15°.
又∵∠BAP=∠APC-∠ABC=15°,
∴∠ABD=∠BAP.
∴AD=BD.
∴AD=CD.
∴∠DAC=∠DCA=45°.
∴∠ACB=45°+30°=75°.
再 见
