2021-2022学年人教版八年级数学上册13.1.1轴对称-课堂同步 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.1.1轴对称-课堂同步 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 10:50:49 | ||
图片预览



文档简介
2021-2022学年八年级数学上册(人教版)
13.1.1轴对称-课堂同步
时间:60分钟
一、单选题
1.将长方形沿折叠得到如图,若则( )°
A.60 B.50 C.75 D.55
2.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
3.如图,是以直线m为对称轴的轴对称图形,若,,则阴影部分的面积是( )
A.56 B.28 C.14 D.无法确定
4.下列判断正确的有( ).
(1)成轴对称的两个图形的对应点的连线段被对称轴垂直平分;(2)成轴对称的两个图形的对应线段相等,对应角相等;(3)成轴对称的两条线段必在对称轴的异侧;(4)等边三角形是轴对称图形,且有三条对称轴.
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
6.下列选项中的图形均为正多边形,其中恰有4条对称轴的是( )
A. B. C. D.
7.如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
8.下列四种表情图片,其中是轴对称图形的是( )
A. B. C. D.
二、填空题
9.如果一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做__,这条直线就是它的__.
10.在线段 角 圆 长方形 梯形 三角形 等边三角形中,是轴对称图形的有__________个.
11.等边三角形、角、长方形这三个图形中,对称轴最多的是___,它共有__条对称轴.
12.如图,把长方形沿EF对折后使两部分重合,若,则_______.
13.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1=______
14.如图,在四边形ABCD中,AC⊥BD于点E,BE=DE,已知AC=10cm,BD=8cm.则阴影部分的面积为_________.
15.如图所示的组图形中,左、右两个图形成轴对称的是第_________________组.
三、解答题
16.下列图形是轴对称图形吗?如果是,画出它们的对称轴.
17.指出图中各有多少条对称轴.
(1) (2) (3)
(4) (5) (6)
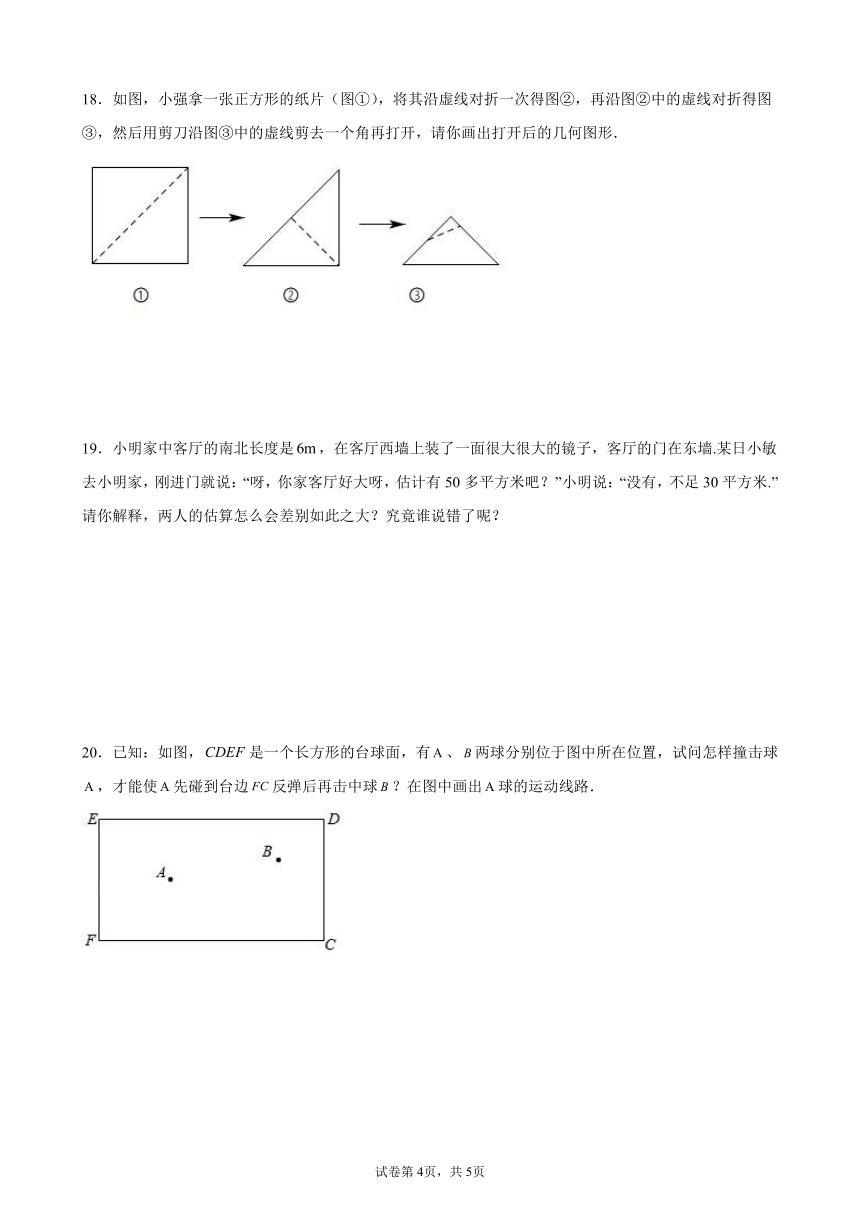
18.如图,小强拿一张正方形的纸片(图①),将其沿虚线对折一次得图②,再沿图②中的虚线对折得图③,然后用剪刀沿图③中的虚线剪去一个角再打开,请你画出打开后的几何图形.
19.小明家中客厅的南北长度是,在客厅西墙上装了一面很大很大的镜子,客厅的门在东墙.某日小敏去小明家,刚进门就说:“呀,你家客厅好大呀,估计有50多平方米吧?”小明说:“没有,不足30平方米.”请你解释,两人的估算怎么会差别如此之大?究竟谁说错了呢?
20.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
21.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km,北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
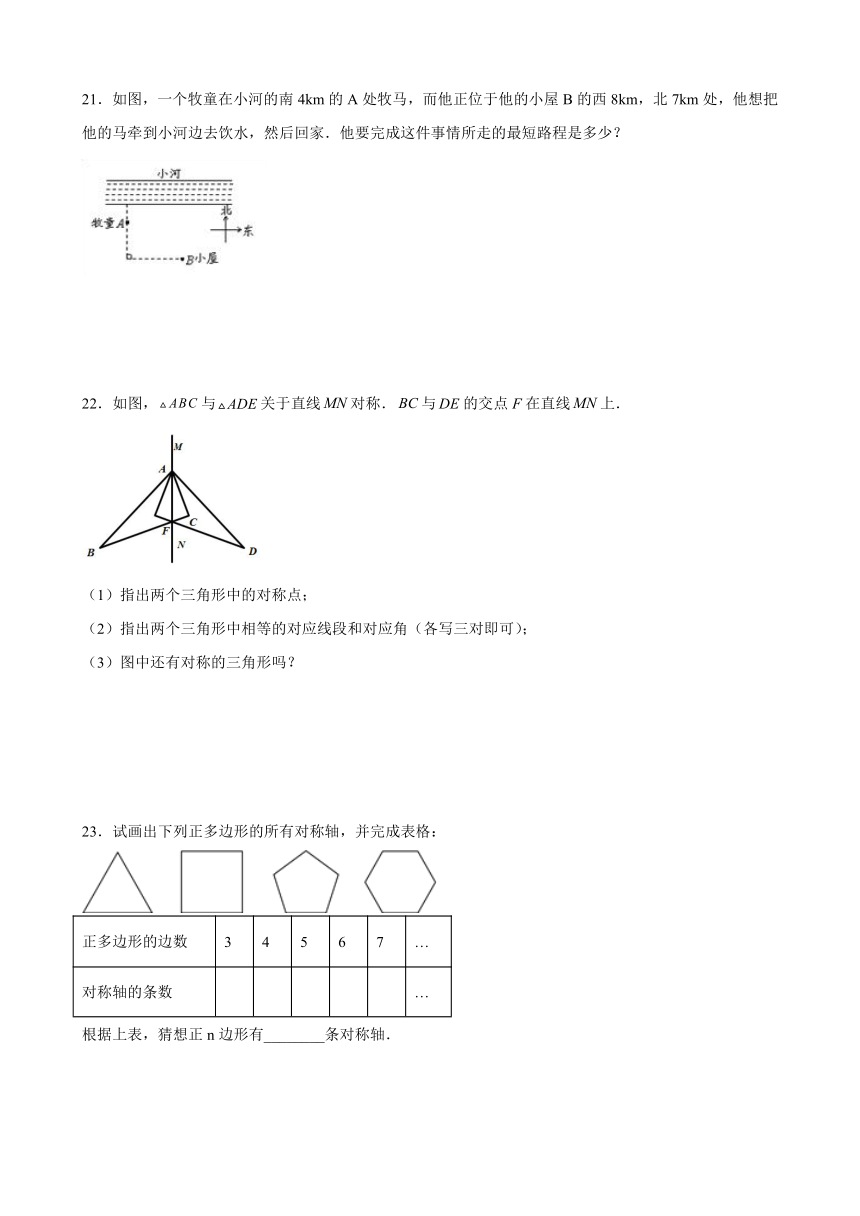
22.如图,与关于直线对称.与的交点F在直线上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的对应线段和对应角(各写三对即可);
(3)图中还有对称的三角形吗?
23.试画出下列正多边形的所有对称轴,并完成表格:
正多边形的边数 3 4 5 6 7 …
对称轴的条数 …
根据上表,猜想正n边形有________条对称轴.
试卷第1页,共3页
参考答案
1.A
【解析】解:∵∠DEC=180°,∠CEF=60°,
∴∠DEF=120°
∵△AEF是由△AED折叠得到,
∴∠AED=∠AEF=∠DEF=60°.
又∵AB//CD
∴
故选择:A
2.B
【解析】解:A、两个全等三角形,一定是轴对称的错误,三角形全等位置上不一定关于某一直线对称,故本选项错误;
B、两个轴对称的三角形,一定全等,正确,故本选项正确;
C、三角形的一条中线把三角形分成以中线为轴对称的两个图形,错误,故本选项错误;
D、三角形的一条高把三角形分成以高线为轴对称的两个图形,错误,故本选项错误.
故选B.
3.C
【解析】∵是以直线m为对称轴的轴对称图形,∴,,∴阴影部分的面积是三角形面积的一半,又∵,∴阴影部分面积.
答案:C
4.C
【解析】解:(1)成轴对称的两个图形的对应点的连线段被对称轴垂直平分,此说法正确;
(2)成轴对称的两个图形的对应线段相等,对应角相等,此说法正确;
(3)成轴对称的两条线段在对称轴的异侧或相交于一点,此说法错误;
(4)等边三角形是轴对称图形,且有三条对称轴,此说法正确.
故选C.
5.D
【解析】选项A,长方形有两条对称轴,选项A错误;
选项B,线段的垂直平分线是这条线段的对称轴,选项B错误;
选项C,角的对称轴是角平分线所在的直线,选项C错误;
选项D,角平分线所在的直线是角的对称轴,选项D正确.
故选D.
6.B
【解析】选项A,正三角形有3条对称轴,故此选项不合题意;
选项B,正方形有4条对称轴,故此选项符合题意;
选项C,正六边形有6条对称轴,故此选项不合题意;
选项D,正八边形有8条对称轴,故此选项不合题意.
故选B.
7.A
【解析】解:根据轴对称的性质可知,台球走过的路径为:
所以球最后将落入的球袋是1号袋,
故选A.
8.A
【解析】解:由轴对称图形的概念可知A是轴对称图形,B,C与D不是轴对称图形.
故选A.
9.轴对称图形 对称轴
【解析】如果一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线就是它的对称轴.
故答案为:轴对称图形;对称轴.
10.5
【解析】解:线段的垂直平分线所在的直线是对称轴,是轴对称图形,符合题意;
角的平分线所在直线就是对称轴,是轴对称图形,符合题意;
圆有无数条对称轴,是轴对称图形,符合题意;
长方形有二条对称轴,是轴对称图形,符合题意;
梯形不一定是轴对称图形,不符合题意;
三角形不一定是轴对称图形,不符合题意;
等边三角形三条中线所在的直线是对称轴,是轴对称图形,符合题意;
故轴对称图形共有5个.
故答案为:5.
11.等边三角形 3
【解析】等边三角形有3条对称轴、,角有1条对称轴,长方形有2条对称轴,故对称轴最多的是等边三角形,它共有3条对称轴.
故答案为等边三角形;3.
12.
【解析】解:如图, ,则
由对折可得:
长方形,
故答案为:
13.60°
【解析】∵台球桌四角都是直角,
∵∠1=∠2,
故答案为
14.
【解析】解:∵AE⊥BD,EB=ED,
∴B,D关于AC轴对称,
∴S阴影=S△ABC=×10×8=20(cm2).
故答案为:20cm2.
15.(3)(4)
【解析】(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
16.第3个图形不是轴对称图形,其余都是.画出对称轴见解析.
【解析】解:根据轴对称图形的意义可知:第3个图形不是轴对称图形,其余都是;
如图:
17.6条,4条,1条,2条,1条,1条
【解析】(1)有6条对称轴;
(2)有4条对称轴;
(3)有1条对称轴;
(4)有2条对称轴;
(5)有1条对称轴;
(6)有1条对称轴.
18.见解析.
【解析】解:如图所示:
19.小敏说错了
【解析】小敏把镜子里看到的都算在一起了,镜子里的虚像使的室内空间在视觉上加倍了,所以小敏误认为有50多平方米,小敏说错了.小明说的是实际面积.
20.见解析
【解析】如图所示:运动路线:.
21.17km.
【解析】作点A 关于直线MN的对称点A’,链接A’B,
则A’B就是所走的最短路程
AA’=4×2=8km
∴A’O= AA’+OA=8+7+15km
由勾股定理得
(A’B)2= (O A’)2+ (OB) 2=152+82=289
∴A’B==17km
22.(1)A→A,B→D,C→E,F→F;(2)AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,∠C=∠E;(3)不另加字母和线段的情况下:△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
【解析】解:①A→A,B→D,C→E,F→F;
②AB=AD,AC=AE,BC=DE,
∠BAC=∠DAE,∠B=∠D,∠C=∠E;
③不另加字母和线段的情况下:△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
23.对称轴见解析;3,4,5,6,7;n.
【解析】解:如图.
故表格中依次填3,4,5,6,7;
猜想正n边形有n条对称轴.
答案第1页,共2页
答案第1页,共2页
13.1.1轴对称-课堂同步
时间:60分钟
一、单选题
1.将长方形沿折叠得到如图,若则( )°
A.60 B.50 C.75 D.55
2.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
3.如图,是以直线m为对称轴的轴对称图形,若,,则阴影部分的面积是( )
A.56 B.28 C.14 D.无法确定
4.下列判断正确的有( ).
(1)成轴对称的两个图形的对应点的连线段被对称轴垂直平分;(2)成轴对称的两个图形的对应线段相等,对应角相等;(3)成轴对称的两条线段必在对称轴的异侧;(4)等边三角形是轴对称图形,且有三条对称轴.
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
6.下列选项中的图形均为正多边形,其中恰有4条对称轴的是( )
A. B. C. D.
7.如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
8.下列四种表情图片,其中是轴对称图形的是( )
A. B. C. D.
二、填空题
9.如果一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做__,这条直线就是它的__.
10.在线段 角 圆 长方形 梯形 三角形 等边三角形中,是轴对称图形的有__________个.
11.等边三角形、角、长方形这三个图形中,对称轴最多的是___,它共有__条对称轴.
12.如图,把长方形沿EF对折后使两部分重合,若,则_______.
13.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1=______
14.如图,在四边形ABCD中,AC⊥BD于点E,BE=DE,已知AC=10cm,BD=8cm.则阴影部分的面积为_________.
15.如图所示的组图形中,左、右两个图形成轴对称的是第_________________组.
三、解答题
16.下列图形是轴对称图形吗?如果是,画出它们的对称轴.
17.指出图中各有多少条对称轴.
(1) (2) (3)
(4) (5) (6)
18.如图,小强拿一张正方形的纸片(图①),将其沿虚线对折一次得图②,再沿图②中的虚线对折得图③,然后用剪刀沿图③中的虚线剪去一个角再打开,请你画出打开后的几何图形.
19.小明家中客厅的南北长度是,在客厅西墙上装了一面很大很大的镜子,客厅的门在东墙.某日小敏去小明家,刚进门就说:“呀,你家客厅好大呀,估计有50多平方米吧?”小明说:“没有,不足30平方米.”请你解释,两人的估算怎么会差别如此之大?究竟谁说错了呢?
20.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
21.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km,北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
22.如图,与关于直线对称.与的交点F在直线上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的对应线段和对应角(各写三对即可);
(3)图中还有对称的三角形吗?
23.试画出下列正多边形的所有对称轴,并完成表格:
正多边形的边数 3 4 5 6 7 …
对称轴的条数 …
根据上表,猜想正n边形有________条对称轴.
试卷第1页,共3页
参考答案
1.A
【解析】解:∵∠DEC=180°,∠CEF=60°,
∴∠DEF=120°
∵△AEF是由△AED折叠得到,
∴∠AED=∠AEF=∠DEF=60°.
又∵AB//CD
∴
故选择:A
2.B
【解析】解:A、两个全等三角形,一定是轴对称的错误,三角形全等位置上不一定关于某一直线对称,故本选项错误;
B、两个轴对称的三角形,一定全等,正确,故本选项正确;
C、三角形的一条中线把三角形分成以中线为轴对称的两个图形,错误,故本选项错误;
D、三角形的一条高把三角形分成以高线为轴对称的两个图形,错误,故本选项错误.
故选B.
3.C
【解析】∵是以直线m为对称轴的轴对称图形,∴,,∴阴影部分的面积是三角形面积的一半,又∵,∴阴影部分面积.
答案:C
4.C
【解析】解:(1)成轴对称的两个图形的对应点的连线段被对称轴垂直平分,此说法正确;
(2)成轴对称的两个图形的对应线段相等,对应角相等,此说法正确;
(3)成轴对称的两条线段在对称轴的异侧或相交于一点,此说法错误;
(4)等边三角形是轴对称图形,且有三条对称轴,此说法正确.
故选C.
5.D
【解析】选项A,长方形有两条对称轴,选项A错误;
选项B,线段的垂直平分线是这条线段的对称轴,选项B错误;
选项C,角的对称轴是角平分线所在的直线,选项C错误;
选项D,角平分线所在的直线是角的对称轴,选项D正确.
故选D.
6.B
【解析】选项A,正三角形有3条对称轴,故此选项不合题意;
选项B,正方形有4条对称轴,故此选项符合题意;
选项C,正六边形有6条对称轴,故此选项不合题意;
选项D,正八边形有8条对称轴,故此选项不合题意.
故选B.
7.A
【解析】解:根据轴对称的性质可知,台球走过的路径为:
所以球最后将落入的球袋是1号袋,
故选A.
8.A
【解析】解:由轴对称图形的概念可知A是轴对称图形,B,C与D不是轴对称图形.
故选A.
9.轴对称图形 对称轴
【解析】如果一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线就是它的对称轴.
故答案为:轴对称图形;对称轴.
10.5
【解析】解:线段的垂直平分线所在的直线是对称轴,是轴对称图形,符合题意;
角的平分线所在直线就是对称轴,是轴对称图形,符合题意;
圆有无数条对称轴,是轴对称图形,符合题意;
长方形有二条对称轴,是轴对称图形,符合题意;
梯形不一定是轴对称图形,不符合题意;
三角形不一定是轴对称图形,不符合题意;
等边三角形三条中线所在的直线是对称轴,是轴对称图形,符合题意;
故轴对称图形共有5个.
故答案为:5.
11.等边三角形 3
【解析】等边三角形有3条对称轴、,角有1条对称轴,长方形有2条对称轴,故对称轴最多的是等边三角形,它共有3条对称轴.
故答案为等边三角形;3.
12.
【解析】解:如图, ,则
由对折可得:
长方形,
故答案为:
13.60°
【解析】∵台球桌四角都是直角,
∵∠1=∠2,
故答案为
14.
【解析】解:∵AE⊥BD,EB=ED,
∴B,D关于AC轴对称,
∴S阴影=S△ABC=×10×8=20(cm2).
故答案为:20cm2.
15.(3)(4)
【解析】(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
16.第3个图形不是轴对称图形,其余都是.画出对称轴见解析.
【解析】解:根据轴对称图形的意义可知:第3个图形不是轴对称图形,其余都是;
如图:
17.6条,4条,1条,2条,1条,1条
【解析】(1)有6条对称轴;
(2)有4条对称轴;
(3)有1条对称轴;
(4)有2条对称轴;
(5)有1条对称轴;
(6)有1条对称轴.
18.见解析.
【解析】解:如图所示:
19.小敏说错了
【解析】小敏把镜子里看到的都算在一起了,镜子里的虚像使的室内空间在视觉上加倍了,所以小敏误认为有50多平方米,小敏说错了.小明说的是实际面积.
20.见解析
【解析】如图所示:运动路线:.
21.17km.
【解析】作点A 关于直线MN的对称点A’,链接A’B,
则A’B就是所走的最短路程
AA’=4×2=8km
∴A’O= AA’+OA=8+7+15km
由勾股定理得
(A’B)2= (O A’)2+ (OB) 2=152+82=289
∴A’B==17km
22.(1)A→A,B→D,C→E,F→F;(2)AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,∠C=∠E;(3)不另加字母和线段的情况下:△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
【解析】解:①A→A,B→D,C→E,F→F;
②AB=AD,AC=AE,BC=DE,
∠BAC=∠DAE,∠B=∠D,∠C=∠E;
③不另加字母和线段的情况下:△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
23.对称轴见解析;3,4,5,6,7;n.
【解析】解:如图.
故表格中依次填3,4,5,6,7;
猜想正n边形有n条对称轴.
答案第1页,共2页
答案第1页,共2页
