湖南省澧县张公庙中学2021—2022学年湘教版九年级数学上册期中复习综合试题(二)(Word版 含答案)
文档属性
| 名称 | 湖南省澧县张公庙中学2021—2022学年湘教版九年级数学上册期中复习综合试题(二)(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 11:52:47 | ||
图片预览




文档简介
湖南省澧县张公庙中学2021—2022学年湘教版九年级数学上册期中复习综合试题(二)与简答
时量120分钟,满分120分
一.选择题(共8小题,每小题3分,共24分)
1.点、、都在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
2.用配方法解一元二次方程,可变形为
A. B. C. D.
3.如图,与位似,其位似中心为点,且为的中点,则与的面积比是
A. B. C. D.
4.如图,中,点、分别在、边上,则下列条件中,不一定能使的是
A. B. C. D.
5.函数与在同一平面直角坐标系的图象可能是
A. B.
C. D.
6.若一元二次方程的系数满足,则方程根的情况是
A.没有实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.无法判断
7.根据中国人民政治协商会议第一届全体会议主席团1949年9月27日公布的国旗制法说明,我国五种规格的国旗旗面为相似矩形,已知一号国旗的标准尺寸是长,高,则如图国旗尺寸不符合标准的是
A. B.
C. D.
8.如图,在平面直角坐标系中,的顶点,分别在轴、轴上,,,斜边轴.若反比例函数的图象经过的中点,则的值
为
A.4 B.5 C.6 D.8
二.填空题(共8小题,每小题3分,共24分)
9.若,,,是比例线段且,,,则 .
10.一元二次方程,化为一元二次方程的一般形式是 .
11.两个相似三角形的相似比是,第一个三角形的最大边长,第二个三角形的最大边长 .
12.若双曲线向右平移2个单位后经过点,则的值是 .
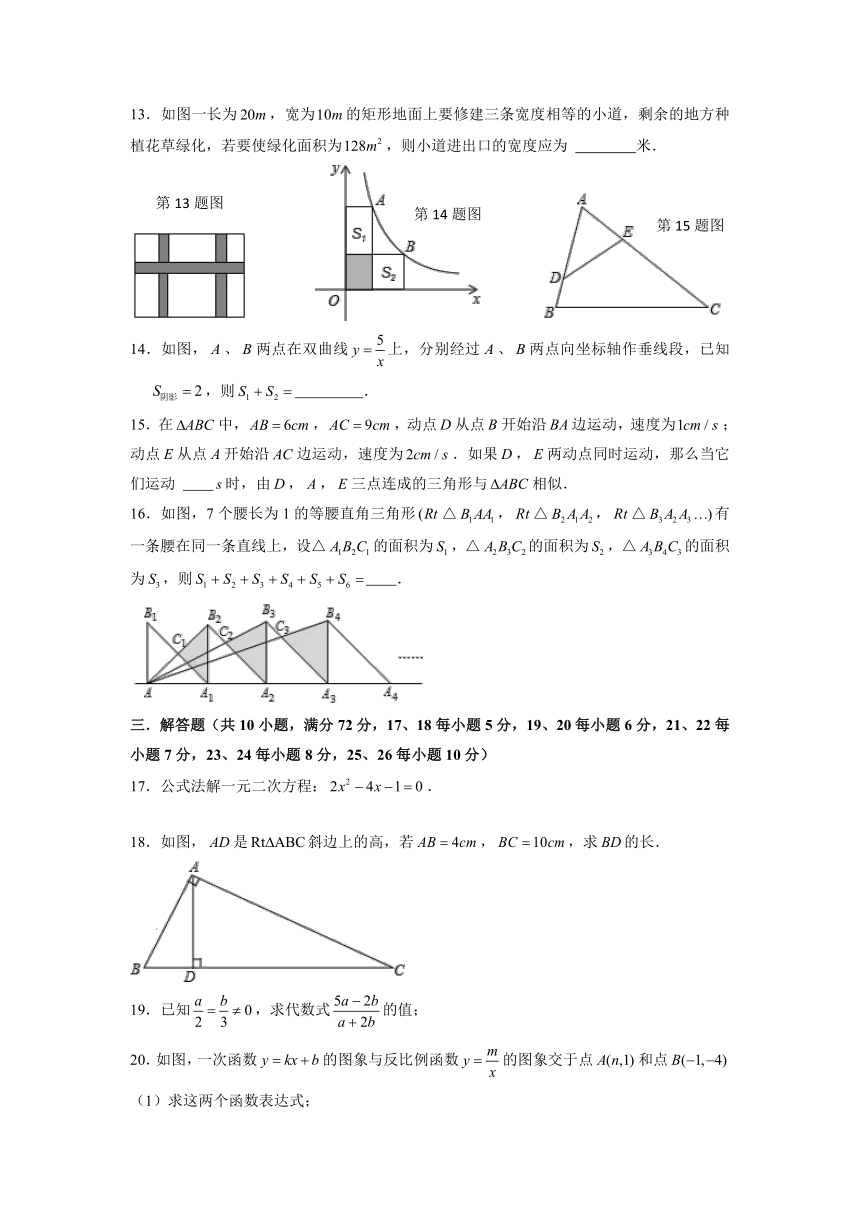
13.如图一长为,宽为的矩形地面上要修建三条宽度相等的小道,剩余的地方种植花草绿化,若要使绿化面积为,则小道进出口的宽度应为 米.
14.如图,、两点在双曲线上,分别经过、两点向坐标轴作垂线段,已知,则 .
15.在中,,,动点从点开始沿边运动,速度为;动点从点开始沿边运动,速度为.如果,两动点同时运动,那么当它们运动 时,由,,三点连成的三角形与相似.
16.如图,7个腰长为1的等腰直角三角形△,△,△有一条腰在同一条直线上,设△的面积为,△的面积为,△的面积为,则 .
三.解答题(共10小题,满分72分,17、18每小题5分,19、20每小题6分,21、22每小题7分,23、24每小题8分,25、26每小题10分)
17.公式法解一元二次方程:.
18.如图,是斜边上的高,若,,求的长.
19.已知,求代数式的值;
20.如图,一次函数的图象与反比例函数的图象交于点和点
(1)求这两个函数表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
21.先化简再求值:已知是方程的解,求代数式的值.
22.如图,已知,,,,.
(1)求和的大小;
(2)求的长.
23.已知关于的一元二次方程有实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,,且,求的取值范围.
24.为预防新冠病毒,零陵区某中学定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间之间成一次函数关系:燃烧完后与时间之间成反比例函数关系,根据图象解答下列问题:
(1)求药物燃烧完后与时间的函数表达式;
(2)当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
25.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒天,但是每增加1条生产线,每条生产线的产能将减少500盒天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
26.如图,在正方形中,是边上的一个动点与,均不重合),将线段绕点顺时针旋转后,得到线段,且交于点,过点作的延长线于点,连接,.
(1)求证:且;
(2)当点在何处时,?请说明理由.
湖南省澧县张公庙中学2021—2022学年湘教版九年级数学上册期中复习综合试题(二)参考简答
一.选择题(共8小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
二.填空题(共8小题)
9. 18 . 10. . 11. . 12. 3 .
13. 2 . 14. 6 . 15. 或 .
16. .
【解】:连接、、、.
个边长为1的等腰三角形有一条边在同一直线上,
,,,,
连接、、点,显然它们共线且平行于
易知,
,
△△,
,
,
同理可求,,,,,
,
三.解答题(共10小题)
17.解一元二次方程:.
【解】:这里,,,
△,
,
解得:,.
18.如图,是斜边上的高,若,,求的长.
【解】:由射影定理得,,
则.
19.已知,求代数式的值;
【解】:设,可得:,,
把,代入.
20.如图,一次函数的图象与反比例函数的图象交于点和点
(1)求这两个函数表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
【解】:(1)点在反比例函数的图象上,
,
反比例函数解析式为:.
点在上,
.
.
将点,代入,得.
.
一次函数的解析式为:.
(2)一次函数的值大于反比例函数的值的的取值范围为:或.
21.先化简再求值:已知是方程的解,求代数式的值.
【解】:原式
,
是方程的解,
,
,
原式.
22.如图,已知,,,,.
(1)求和的大小;
(2)求的长.
【解】:(1),
,
,
,
,
,;
(2)由得,
23.已知关于的一元二次方程有实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,,且,求的取值范围.
【解】:(1)方程有实数根,
△,
解得:.
故的取值范围是;
(2),是方程的两个实数根,
,,
,
,
解得,
由(1)可得,
的取值范围是.
24.为预防新冠病毒,零陵区某中学定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间之间成一次函数关系:燃烧完后与时间之间成反比例函数关系,根据图象解答下列问题:
(1)求药物燃烧完后与时间的函数表达式;
(2)当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
【解】:设药物燃烧阶段与的函数关系式为,
将,代人得:,
解得:,
解析式为,
当时,,
点的坐标为,设药物燃烧后的解析式为,
代人得,
反比例函数的解析式为;
(2)令中,得,
令中,得,
所以从消毒开始,第2至6分钟,消毒人员不能留在教室.
25.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒天,但是每增加1条生产线,每条生产线的产能将减少500盒天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
【解】:(1)设每天增长的百分率为,
依题意得:,
,(不合题意,舍去).
答:每天增长的百分率为.
(2)设增加条生产线,则每条生产线的产量为盒天,
依题意得:,
整理得:,
解得:,.
又要节省投入,
.
答:应该增加4条生产线.
26.如图,在正方形中,是边上的一个动点与,均不重合),将线段绕点顺时针旋转后,得到线段,且交于点,过点作的延长线于点,连接,.
(1)求证:且;
(2)当点在何处时,?请说明理由.
【解】:(1)证明:在正方形中,在边上,且,
,
,
,
,
在和中, ,
,
,
又,
四边形是平行四边形,
,,
,
.
(2)当点是的中点时,.
理由:,
,
,,
,
,
,
,
即点是边的中点,
当点恰好是边的中点时,.
第4题图
第3题图
第15题图
第14题图
第13题图
时量120分钟,满分120分
一.选择题(共8小题,每小题3分,共24分)
1.点、、都在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
2.用配方法解一元二次方程,可变形为
A. B. C. D.
3.如图,与位似,其位似中心为点,且为的中点,则与的面积比是
A. B. C. D.
4.如图,中,点、分别在、边上,则下列条件中,不一定能使的是
A. B. C. D.
5.函数与在同一平面直角坐标系的图象可能是
A. B.
C. D.
6.若一元二次方程的系数满足,则方程根的情况是
A.没有实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.无法判断
7.根据中国人民政治协商会议第一届全体会议主席团1949年9月27日公布的国旗制法说明,我国五种规格的国旗旗面为相似矩形,已知一号国旗的标准尺寸是长,高,则如图国旗尺寸不符合标准的是
A. B.
C. D.
8.如图,在平面直角坐标系中,的顶点,分别在轴、轴上,,,斜边轴.若反比例函数的图象经过的中点,则的值
为
A.4 B.5 C.6 D.8
二.填空题(共8小题,每小题3分,共24分)
9.若,,,是比例线段且,,,则 .
10.一元二次方程,化为一元二次方程的一般形式是 .
11.两个相似三角形的相似比是,第一个三角形的最大边长,第二个三角形的最大边长 .
12.若双曲线向右平移2个单位后经过点,则的值是 .
13.如图一长为,宽为的矩形地面上要修建三条宽度相等的小道,剩余的地方种植花草绿化,若要使绿化面积为,则小道进出口的宽度应为 米.
14.如图,、两点在双曲线上,分别经过、两点向坐标轴作垂线段,已知,则 .
15.在中,,,动点从点开始沿边运动,速度为;动点从点开始沿边运动,速度为.如果,两动点同时运动,那么当它们运动 时,由,,三点连成的三角形与相似.
16.如图,7个腰长为1的等腰直角三角形△,△,△有一条腰在同一条直线上,设△的面积为,△的面积为,△的面积为,则 .
三.解答题(共10小题,满分72分,17、18每小题5分,19、20每小题6分,21、22每小题7分,23、24每小题8分,25、26每小题10分)
17.公式法解一元二次方程:.
18.如图,是斜边上的高,若,,求的长.
19.已知,求代数式的值;
20.如图,一次函数的图象与反比例函数的图象交于点和点
(1)求这两个函数表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
21.先化简再求值:已知是方程的解,求代数式的值.
22.如图,已知,,,,.
(1)求和的大小;
(2)求的长.
23.已知关于的一元二次方程有实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,,且,求的取值范围.
24.为预防新冠病毒,零陵区某中学定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间之间成一次函数关系:燃烧完后与时间之间成反比例函数关系,根据图象解答下列问题:
(1)求药物燃烧完后与时间的函数表达式;
(2)当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
25.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒天,但是每增加1条生产线,每条生产线的产能将减少500盒天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
26.如图,在正方形中,是边上的一个动点与,均不重合),将线段绕点顺时针旋转后,得到线段,且交于点,过点作的延长线于点,连接,.
(1)求证:且;
(2)当点在何处时,?请说明理由.
湖南省澧县张公庙中学2021—2022学年湘教版九年级数学上册期中复习综合试题(二)参考简答
一.选择题(共8小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
二.填空题(共8小题)
9. 18 . 10. . 11. . 12. 3 .
13. 2 . 14. 6 . 15. 或 .
16. .
【解】:连接、、、.
个边长为1的等腰三角形有一条边在同一直线上,
,,,,
连接、、点,显然它们共线且平行于
易知,
,
△△,
,
,
同理可求,,,,,
,
三.解答题(共10小题)
17.解一元二次方程:.
【解】:这里,,,
△,
,
解得:,.
18.如图,是斜边上的高,若,,求的长.
【解】:由射影定理得,,
则.
19.已知,求代数式的值;
【解】:设,可得:,,
把,代入.
20.如图,一次函数的图象与反比例函数的图象交于点和点
(1)求这两个函数表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
【解】:(1)点在反比例函数的图象上,
,
反比例函数解析式为:.
点在上,
.
.
将点,代入,得.
.
一次函数的解析式为:.
(2)一次函数的值大于反比例函数的值的的取值范围为:或.
21.先化简再求值:已知是方程的解,求代数式的值.
【解】:原式
,
是方程的解,
,
,
原式.
22.如图,已知,,,,.
(1)求和的大小;
(2)求的长.
【解】:(1),
,
,
,
,
,;
(2)由得,
23.已知关于的一元二次方程有实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,,且,求的取值范围.
【解】:(1)方程有实数根,
△,
解得:.
故的取值范围是;
(2),是方程的两个实数根,
,,
,
,
解得,
由(1)可得,
的取值范围是.
24.为预防新冠病毒,零陵区某中学定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间之间成一次函数关系:燃烧完后与时间之间成反比例函数关系,根据图象解答下列问题:
(1)求药物燃烧完后与时间的函数表达式;
(2)当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
【解】:设药物燃烧阶段与的函数关系式为,
将,代人得:,
解得:,
解析式为,
当时,,
点的坐标为,设药物燃烧后的解析式为,
代人得,
反比例函数的解析式为;
(2)令中,得,
令中,得,
所以从消毒开始,第2至6分钟,消毒人员不能留在教室.
25.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒天,但是每增加1条生产线,每条生产线的产能将减少500盒天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
【解】:(1)设每天增长的百分率为,
依题意得:,
,(不合题意,舍去).
答:每天增长的百分率为.
(2)设增加条生产线,则每条生产线的产量为盒天,
依题意得:,
整理得:,
解得:,.
又要节省投入,
.
答:应该增加4条生产线.
26.如图,在正方形中,是边上的一个动点与,均不重合),将线段绕点顺时针旋转后,得到线段,且交于点,过点作的延长线于点,连接,.
(1)求证:且;
(2)当点在何处时,?请说明理由.
【解】:(1)证明:在正方形中,在边上,且,
,
,
,
,
在和中, ,
,
,
又,
四边形是平行四边形,
,,
,
.
(2)当点是的中点时,.
理由:,
,
,,
,
,
,
,
即点是边的中点,
当点恰好是边的中点时,.
第4题图
第3题图
第15题图
第14题图
第13题图
同课章节目录
