2021-2022学年度人教版八年级数学上册课件: 15.3 第2课时 分式方程的应用(23张)
文档属性
| 名称 | 2021-2022学年度人教版八年级数学上册课件: 15.3 第2课时 分式方程的应用(23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 940.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:16:41 | ||
图片预览







文档简介
(共23张PPT)
RJ八(上)
教学课件
第十五章 分 式
15.3 分式方程
第2课时 分式方程的应用
1.理解题中数量关系,正确列出分式方程.(重点)
2.能根据不同的实际问题设未知数,列分式方程解决
实际问题.(难点)
学习目标
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
4.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题:路程=速度×时间
(2)数字问题:十进制数的表示法
(3)工程问题:工作量=工时×工效
(4)利润问题:批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价
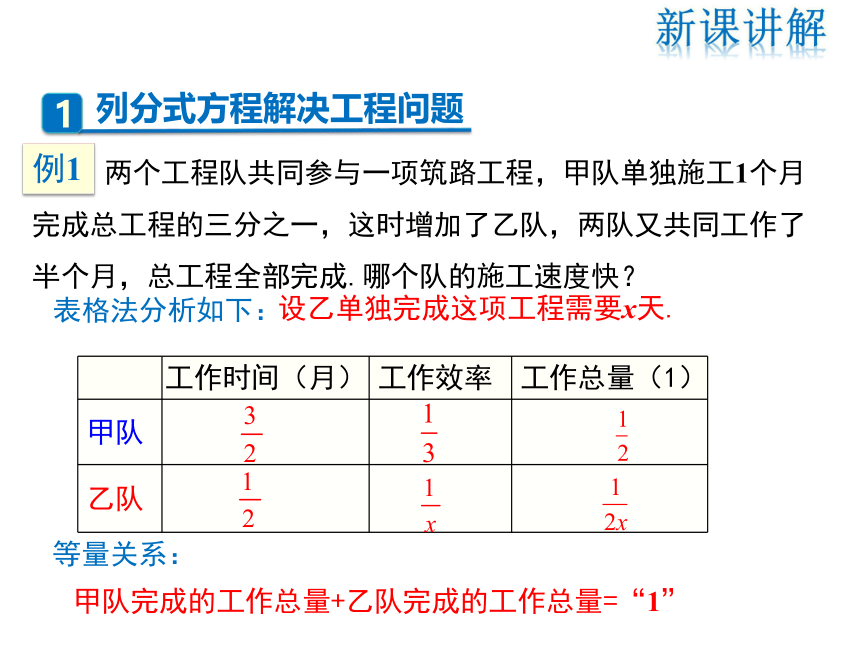
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x天.
列分式方程解决工程问题
1
例1
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意,得
即
方程两边都乘6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
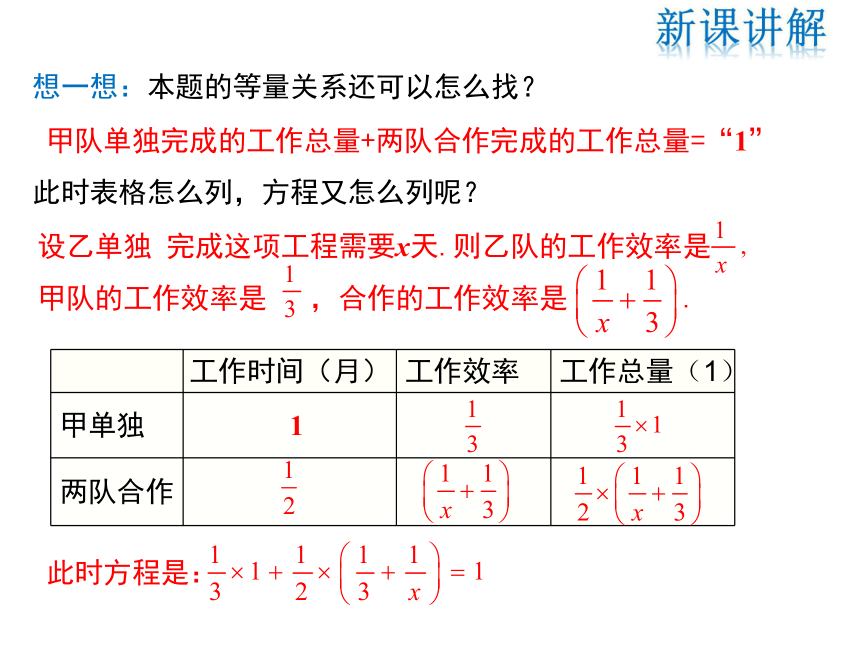
想一想:本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
此时表格怎么列,方程又怎么列呢?
工作时间(月) 工作效率 工作总量(1)
甲单独
两队合作
设乙单独 完成这项工程需要x天.则乙队的工作效率是 甲队的工作效率是 ,合作的工作效率是 .
此时方程是:
1
★工程问题:
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如×单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率、工作时间、工作量;2指该类问题中的“两个主人公”,如甲队和乙队或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲、乙两队工作效率的和”;
【练习】抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
分析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时,由题意,得
.
解得 x=6.
经检验,x=6是方程的解.∴x+3=9.
故甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车车紧随其后,他们同时出发,当面包车车行驶了200公里时,发现小轿车车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
0
180
200
列分式方程解决行程问题
2
例2
路程 速度 时间
面包车
小轿车
200
180
x+10
x
分析:设小轿车的速度为x千米/小时.
面包车的时间=小轿车的时间
等量关系:
列表格如下:
解:设小轿车的速度为x千米/小时,则面包车速度为x+10千米/小时,依题意,得
解得 x=90.
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
故面包车的速度为100千米/小时,小轿车的速度为90千米/小时.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
【练习】小轿车发现跟丢时,面包车行驶了200公里,小轿车行驶了180公里,小轿车为了追上面包车,他就马上提速,他们约定好在300公里的地方碰头,他们正好同时到达,请问小轿车提速多少km/h?
0
180
200
300
解:设小轿车提速为x千米/小时,依题意,得
解得 x=30.
经检验,x=30是原方程的解,且符合题意.
故小轿车提速为30千米/小时.
★列分式方程解应用题的一般步骤:
1.审:审清题意,并设未知数;
2.找:找出相等关系;
3.列:列出方程;
4.解:解这个分式方程;
5.验:验根(包括两方面 :是否是分式方程的根; 是否符合题意);
6.答:写出答案.
佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
例3
解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,根据题意,得
解得 x=6.
经检验,x=6是原方程的解,且符合题意.
故第一次水果的进价为每千克6元.
(2)第一次购买水果1200÷6=200(千克).
第二次购买水果200+20=220(千克).
第一次赚钱为200×(8-6)=400(元),
第二次赚钱为100×(9-6.6)+120×(9×0.5-6.6)=-12(元).
所以两次共赚钱400-12=388(元).
1.某服装加工厂加工校服960套的订单,原计划每天
做48套.正好按时完成.后因学校要求提前5天交货,
为按时完成订单,设每天就多做x套,则x应满足的方
程为( )
A. B.
C. D.
D
2.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
解:设船在静水中的速度为x千米/小时,根据题意,得
解得 x=±18.
经检验,x=18是原方程的解,且符合题意.
故船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2),得
80x+160 -80x+160=x2 -4.
3. 为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
解:设骑车学生的速度为x千米/时,依题意,得
解得
x=15.
经检验,x=15是原方程的根,且符合题意.
故骑车学生的速度是15千米/时.
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
方法
步骤
一审、二设、三找、四列、五解、六验、七写
321法
RJ八(上)
教学课件
第十五章 分 式
15.3 分式方程
第2课时 分式方程的应用
1.理解题中数量关系,正确列出分式方程.(重点)
2.能根据不同的实际问题设未知数,列分式方程解决
实际问题.(难点)
学习目标
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
4.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题:路程=速度×时间
(2)数字问题:十进制数的表示法
(3)工程问题:工作量=工时×工效
(4)利润问题:批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x天.
列分式方程解决工程问题
1
例1
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意,得
即
方程两边都乘6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
想一想:本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
此时表格怎么列,方程又怎么列呢?
工作时间(月) 工作效率 工作总量(1)
甲单独
两队合作
设乙单独 完成这项工程需要x天.则乙队的工作效率是 甲队的工作效率是 ,合作的工作效率是 .
此时方程是:
1
★工程问题:
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如×单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率、工作时间、工作量;2指该类问题中的“两个主人公”,如甲队和乙队或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲、乙两队工作效率的和”;
【练习】抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
分析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时,由题意,得
.
解得 x=6.
经检验,x=6是方程的解.∴x+3=9.
故甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车车紧随其后,他们同时出发,当面包车车行驶了200公里时,发现小轿车车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
0
180
200
列分式方程解决行程问题
2
例2
路程 速度 时间
面包车
小轿车
200
180
x+10
x
分析:设小轿车的速度为x千米/小时.
面包车的时间=小轿车的时间
等量关系:
列表格如下:
解:设小轿车的速度为x千米/小时,则面包车速度为x+10千米/小时,依题意,得
解得 x=90.
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
故面包车的速度为100千米/小时,小轿车的速度为90千米/小时.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
【练习】小轿车发现跟丢时,面包车行驶了200公里,小轿车行驶了180公里,小轿车为了追上面包车,他就马上提速,他们约定好在300公里的地方碰头,他们正好同时到达,请问小轿车提速多少km/h?
0
180
200
300
解:设小轿车提速为x千米/小时,依题意,得
解得 x=30.
经检验,x=30是原方程的解,且符合题意.
故小轿车提速为30千米/小时.
★列分式方程解应用题的一般步骤:
1.审:审清题意,并设未知数;
2.找:找出相等关系;
3.列:列出方程;
4.解:解这个分式方程;
5.验:验根(包括两方面 :是否是分式方程的根; 是否符合题意);
6.答:写出答案.
佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
例3
解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,根据题意,得
解得 x=6.
经检验,x=6是原方程的解,且符合题意.
故第一次水果的进价为每千克6元.
(2)第一次购买水果1200÷6=200(千克).
第二次购买水果200+20=220(千克).
第一次赚钱为200×(8-6)=400(元),
第二次赚钱为100×(9-6.6)+120×(9×0.5-6.6)=-12(元).
所以两次共赚钱400-12=388(元).
1.某服装加工厂加工校服960套的订单,原计划每天
做48套.正好按时完成.后因学校要求提前5天交货,
为按时完成订单,设每天就多做x套,则x应满足的方
程为( )
A. B.
C. D.
D
2.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
解:设船在静水中的速度为x千米/小时,根据题意,得
解得 x=±18.
经检验,x=18是原方程的解,且符合题意.
故船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2),得
80x+160 -80x+160=x2 -4.
3. 为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
解:设骑车学生的速度为x千米/时,依题意,得
解得
x=15.
经检验,x=15是原方程的根,且符合题意.
故骑车学生的速度是15千米/时.
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
方法
步骤
一审、二设、三找、四列、五解、六验、七写
321法
