4.3.2 一次函数的图象 课件(共22张PPT)
文档属性
| 名称 | 4.3.2 一次函数的图象 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 48.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
北师版八年级上册 函数
§4.3.2 一次函数
一次函数的图像和性质
温故知新
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
学习目标
(1)理解一次函数和正比例函数的图像关系;
(2)掌握一次函数的图像画法——两点法;
(3)掌握一次函数的图像性质,并能灵活使用.
新知导入
1、什么是一次函数?
2、正比例函数y=kx(k≠0)的图象与性质有哪些?
一般地,形如_________(k、b 是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即_______ , 所以____________是一种特殊的一次函数
y=kx
y=kx+b
正比例函数
温故知新
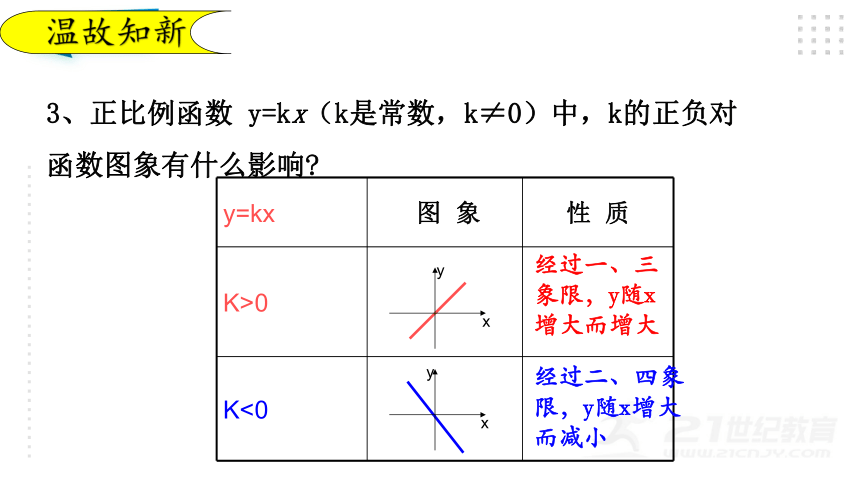
y=kx 图 象 性 质
K>0
K<0
经过一、三象限,y随x增大而增大
经过二、四象限,y随x增大而减小
3、正比例函数 y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响
y
x
y
x
温故知新
正比例函数是 的一次函数,
它们图象之间有什么关系
一次函数又有什么性质呢
正比例函数的图像是 ;
那么一次函数的图象也会是一条直线吗?
是
一条直线
第一篇:
k相同, 图平行
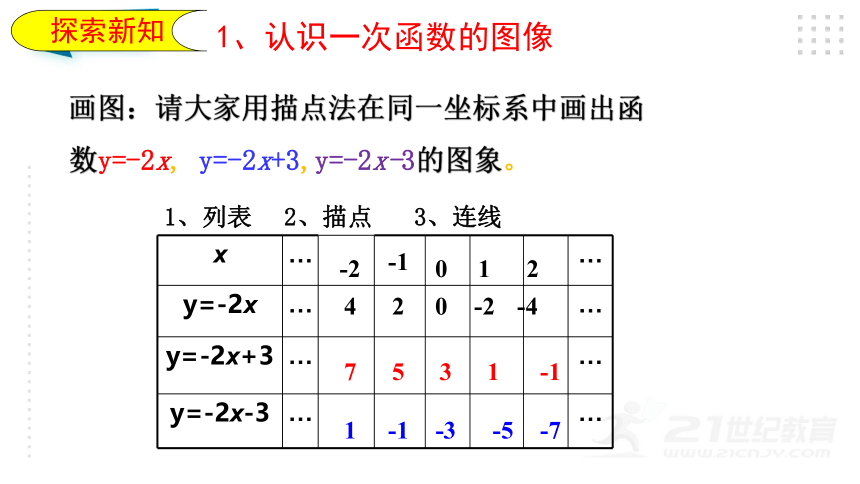
画图:请大家用描点法在同一坐标系中画出函数y=-2x, y=-2x+3,y=-2x-3的图象。
1、列表
2、描点
3、连线
x … …
y=-2x … …
y=-2x+3 … …
y=-2x-3 … …
4
7
-1
2
5
1
0
3
-3
-2
1
-5
-4
-1
-7
-2
-1
0
2
1
1、认识一次函数的图像
探索新知
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
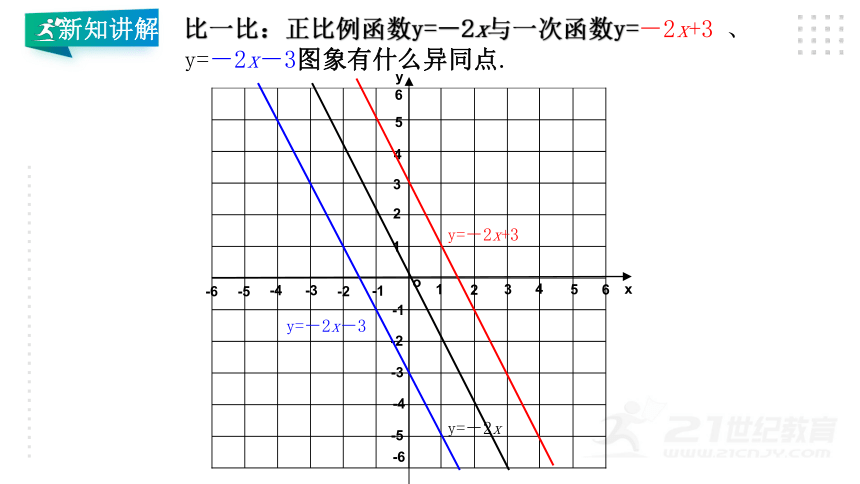
y=-2x
y=-2x+3
y=-2x-3
比一比:正比例函数y=-2x与一次函数y=-2x+3 、
y=-2x-3图象有什么异同点.
新知讲解
(1) 所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx________
而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移b个单位。
反思回顾
图象平移口诀:上加下减
第二篇 两点法
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
“两点法”画一次函数图象
新知讲解
画一次函数的图象时,通常我们可以选
这两个点,来描点、连线。
x 0
y=Kx+b 0
反思回顾
第三篇
一次函数图象与性质
体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1 的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
3、学习一次函数性质
新知讲解
k<0,b<0
一次函数y=kx+b(k、b是常数,k≠0)的图象
k>0,b>0
k>0,b<0
k<0,b>0
图象经过
一,二,三象限
图象经过
一,三,四象限
图象经过
一,二,四象限
图象经过
二,三,四象限
y随x的增大
而增大
y随x的增大
而增大
y随x的增大
而减小
y随x的增大
而减小
x
y
0
(0,b)
y
x
0
(0,b)
x
y
0
(0,b)
x
y
0
(0,b)
当b>0时,交点在原点上方.
当b=0时,交点即原点.
当b<0时,交点在原点下方.
2、b决定直线y=kx+b与y轴交点的坐标(0,b).
反思回顾
k、b对直线y=kx+b的影响
1、k决定了
①图象经过的象限;
②y与x的增减性;
①k>0,增而增
②k<0,过二、四
①k>0,过一、三
②k<0,增而减
1.直线y=2x-3与x轴交点坐标为_______,与y轴交点坐标为_____,图象经过第____ _象限,y随x增大而_________.
2.分别说出满足下列条件的一次函数的图象过哪几个象限?
(1)k>0 b>0 (2)k>0 b<0
(3)k<0 b>0 (4)k<0 b<0
课堂练习
(1.5,0)
(0,-3)
一、三、四
增大
一、三、二
一、三、四
一、二、四
二、三、四
3、已知函数y=(m-2)x+n的图象经过一、二、三象限.
求 : m、n的取值范围.
课堂练习
解:由题意得:
m-2>0, n>0
∴m>2 n>0
1.下列各点中,那些点在函数y=4x+1的图象上 那些不在函数的图象上 (2, 9) (5,1) (-1,-3) (-0.5,-1)
2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= ,b= .
3.点已知M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 .
课堂练习:
-1
2.5
-1
课堂小结
告诉大家本节课你的收获!
3.会用:一次函数的图象、性质
1.会画:用两点法画一次函数的图象
2.会求:一次函数与坐标轴的交点
y
x
o
2
1
·
·
y=x+1
x
y
y
o
2
·
·
y=2x-1
x
y
y
o
2
·
·
y=-2x+1
x
y
y
o
2
·
·
y=-x-1
x
y
图象经过的象限
k的符号
b的符号
一、二、三
一、三、四
一、二、四
二、三、四
k>0
b>0
k>0
k<0
k<0
b>0
b<0
b<0
直线经过的象限
你学会了吗?
北师版八年级上册 函数
§4.3.2 一次函数
一次函数的图像和性质
温故知新
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
学习目标
(1)理解一次函数和正比例函数的图像关系;
(2)掌握一次函数的图像画法——两点法;
(3)掌握一次函数的图像性质,并能灵活使用.
新知导入
1、什么是一次函数?
2、正比例函数y=kx(k≠0)的图象与性质有哪些?
一般地,形如_________(k、b 是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即_______ , 所以____________是一种特殊的一次函数
y=kx
y=kx+b
正比例函数
温故知新
y=kx 图 象 性 质
K>0
K<0
经过一、三象限,y随x增大而增大
经过二、四象限,y随x增大而减小
3、正比例函数 y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响
y
x
y
x
温故知新
正比例函数是 的一次函数,
它们图象之间有什么关系
一次函数又有什么性质呢
正比例函数的图像是 ;
那么一次函数的图象也会是一条直线吗?
是
一条直线
第一篇:
k相同, 图平行
画图:请大家用描点法在同一坐标系中画出函数y=-2x, y=-2x+3,y=-2x-3的图象。
1、列表
2、描点
3、连线
x … …
y=-2x … …
y=-2x+3 … …
y=-2x-3 … …
4
7
-1
2
5
1
0
3
-3
-2
1
-5
-4
-1
-7
-2
-1
0
2
1
1、认识一次函数的图像
探索新知
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=-2x
y=-2x+3
y=-2x-3
比一比:正比例函数y=-2x与一次函数y=-2x+3 、
y=-2x-3图象有什么异同点.
新知讲解
(1) 所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx________
而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移b个单位。
反思回顾
图象平移口诀:上加下减
第二篇 两点法
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
“两点法”画一次函数图象
新知讲解
画一次函数的图象时,通常我们可以选
这两个点,来描点、连线。
x 0
y=Kx+b 0
反思回顾
第三篇
一次函数图象与性质
体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1 的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
3、学习一次函数性质
新知讲解
k<0,b<0
一次函数y=kx+b(k、b是常数,k≠0)的图象
k>0,b>0
k>0,b<0
k<0,b>0
图象经过
一,二,三象限
图象经过
一,三,四象限
图象经过
一,二,四象限
图象经过
二,三,四象限
y随x的增大
而增大
y随x的增大
而增大
y随x的增大
而减小
y随x的增大
而减小
x
y
0
(0,b)
y
x
0
(0,b)
x
y
0
(0,b)
x
y
0
(0,b)
当b>0时,交点在原点上方.
当b=0时,交点即原点.
当b<0时,交点在原点下方.
2、b决定直线y=kx+b与y轴交点的坐标(0,b).
反思回顾
k、b对直线y=kx+b的影响
1、k决定了
①图象经过的象限;
②y与x的增减性;
①k>0,增而增
②k<0,过二、四
①k>0,过一、三
②k<0,增而减
1.直线y=2x-3与x轴交点坐标为_______,与y轴交点坐标为_____,图象经过第____ _象限,y随x增大而_________.
2.分别说出满足下列条件的一次函数的图象过哪几个象限?
(1)k>0 b>0 (2)k>0 b<0
(3)k<0 b>0 (4)k<0 b<0
课堂练习
(1.5,0)
(0,-3)
一、三、四
增大
一、三、二
一、三、四
一、二、四
二、三、四
3、已知函数y=(m-2)x+n的图象经过一、二、三象限.
求 : m、n的取值范围.
课堂练习
解:由题意得:
m-2>0, n>0
∴m>2 n>0
1.下列各点中,那些点在函数y=4x+1的图象上 那些不在函数的图象上 (2, 9) (5,1) (-1,-3) (-0.5,-1)
2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= ,b= .
3.点已知M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 .
课堂练习:
-1
2.5
-1
课堂小结
告诉大家本节课你的收获!
3.会用:一次函数的图象、性质
1.会画:用两点法画一次函数的图象
2.会求:一次函数与坐标轴的交点
y
x
o
2
1
·
·
y=x+1
x
y
y
o
2
·
·
y=2x-1
x
y
y
o
2
·
·
y=-2x+1
x
y
y
o
2
·
·
y=-x-1
x
y
图象经过的象限
k的符号
b的符号
一、二、三
一、三、四
一、二、四
二、三、四
k>0
b>0
k>0
k<0
k<0
b>0
b<0
b<0
直线经过的象限
你学会了吗?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
