2021-2022学年高中数学(人教A版2019)必修第二册8.5.2直线与平面平行 第2课时 直线与平面平行的性质 教案
文档属性
| 名称 | 2021-2022学年高中数学(人教A版2019)必修第二册8.5.2直线与平面平行 第2课时 直线与平面平行的性质 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 22:14:40 | ||
图片预览

文档简介
8.5.2直线与平面平行
第二课时 直线与平面平行的性质
一、教学目标 1. 掌握空间平面与平面平行的判定定理,并能应用这个定理解决问题
2. 平面与平面平行的判定定理的应用
3. 进一步培养学生观察、发现问题的能力和空间想象能力
二、教学重点 空间平面与平面平行的判定定理
教学难点 应用平面与平面平行的判定定理解决问题
三、教学过程
1、复习回顾情境引入
问题1:直线与平面平行的判定定理
答:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行
问题2:如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?
答:
问题3:什么条件下,平面内的直线与直线a平行呢?引出下面问题:
已知:,求证:
证明:∵
∴
又
∴a与b无公共点
又
∴
2、探索新知
1)直线与平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行
符号表述:a∥α,a β,α∩β=b a∥b
简记:线线平行 线面平行
注意:①定理中三个条件缺一不可
②简记:线面平行,则线线平行
③定理的作用:判断直线与直线平行的重要依据
④定理的关键:寻找平面与平面的交线
【例1】如右图的一块木料中,棱BC平行面A'C'
(1)要经过面A'C'内的一点P和棱BC将木料锯开,在木料表面应该怎样画线
(2)所画的线与平面AC是什么位置关系
解:(1)如右图,在平面A'C内,过点P作直线EF,使EF//B'C',并分别
交棱A'B'、D'C' 于点E、F.连接BE、CF,则EF、BE、 CF就是应
画的线
(2) ∵BC∥平面A'C',平面BC'平面A'C'=B'C'
∴BC//B'C'
由(1)知EF//B'C'
∴EF//BC,而BC 平面AC,EF 平面AC
∴EF//平面AC
显然,BE、CF都与平面AC相交
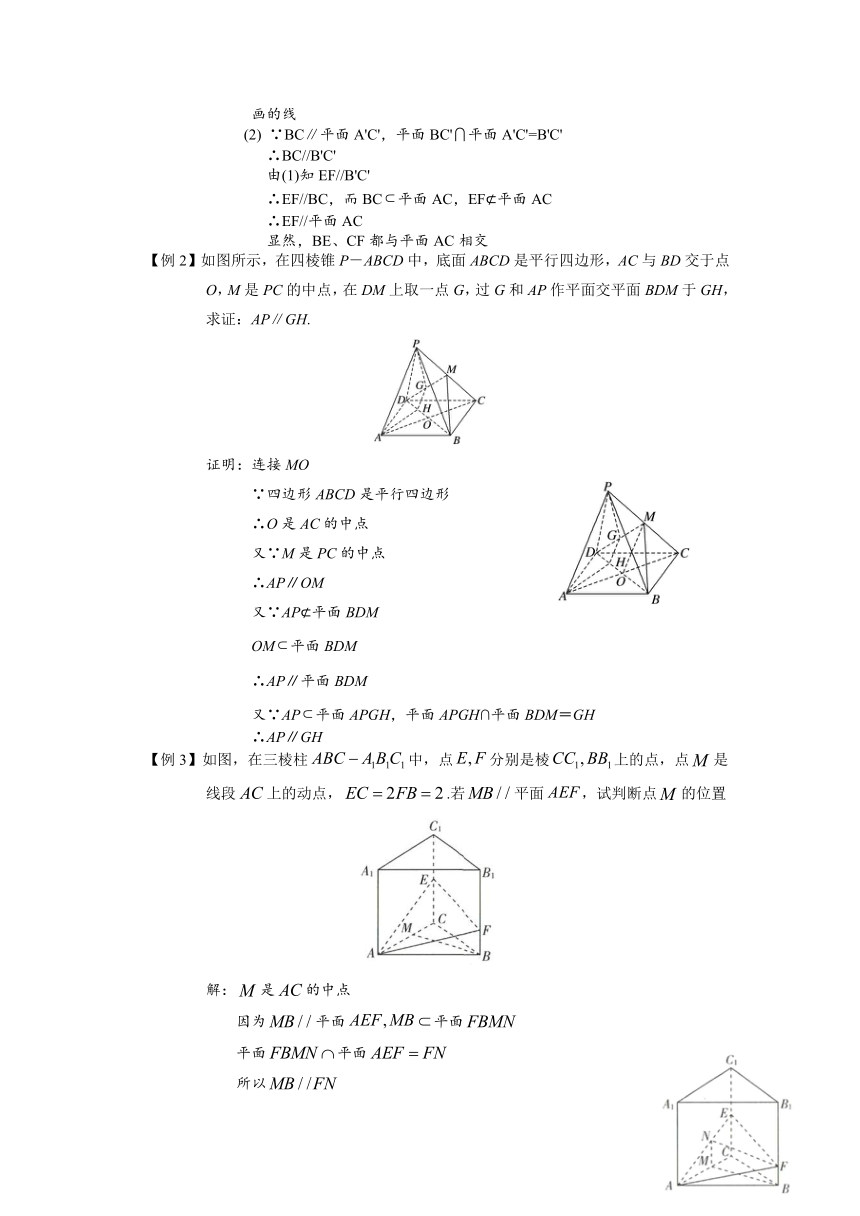
【例2】如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.
证明:连接MO
∵四边形ABCD是平行四边形
∴O是AC的中点
又∵M是PC的中点
∴AP∥OM
又∵AP 平面BDM
OM 平面BDM
∴AP∥平面BDM
又∵AP 平面APGH,平面APGH∩平面BDM=GH
∴AP∥GH
【例3】如图,在三棱柱中,点分别是棱上的点,点是线段上的动点,.若平面,试判断点的位置
解:是的中点
因为平面平面
平面平面
所以
所以四边形是平行四边形
所以
而
所以
故是的中位线
所以是的中点时,平面
方法规律:线面平行的性质和判定经常交替使用,也就是通过线线平行得到线面平行,再通过线面平行得线线平
行.利用线面平行的性质定理解题的具体步骤:
(1)确定(或寻找)一条直线平行于一个平面
(2)确定(或寻找)过这条直线且与这个平行平面相交的平面
(3)确定交线
(4)由性质定理得出线线平行的结论
四、课堂练习
P138 练习
1、如图,在五面体EFABCD中,已知四边形ABCD为梯形,AD∥BC,求证:AD∥EF
证明 ∵AD∥BC,AD 平面BCEF,BC 平面BCEF
∴AD∥平面BCEF
∵AD 平面ADEF,平面ADEF∩平面BCEF=EF
∴AD∥EF
2、如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1
证明:取D1B1的中点O,连接OF,OB(图略)
∵F为C1D1的中点
∴OF∥B1C1且OF=B1C1
又BE∥B1C1,BE=B1C1
∴OF∥BE且OF=BE
∴四边形OFEB是平行四边形,∴EF∥BO
∵EF 平面BDD1B1,BO 平面BDD1B1
∴EF∥平面BDD1B1
五、课堂小结
1、直线与平面平行的性质定理
2、证明线与线、线与面的平行关系的一般规律是:“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段
六、课后作业
习题8.5 7、8
七、课后反思
第二课时 直线与平面平行的性质
一、教学目标 1. 掌握空间平面与平面平行的判定定理,并能应用这个定理解决问题
2. 平面与平面平行的判定定理的应用
3. 进一步培养学生观察、发现问题的能力和空间想象能力
二、教学重点 空间平面与平面平行的判定定理
教学难点 应用平面与平面平行的判定定理解决问题
三、教学过程
1、复习回顾情境引入
问题1:直线与平面平行的判定定理
答:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行
问题2:如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?
答:
问题3:什么条件下,平面内的直线与直线a平行呢?引出下面问题:
已知:,求证:
证明:∵
∴
又
∴a与b无公共点
又
∴
2、探索新知
1)直线与平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行
符号表述:a∥α,a β,α∩β=b a∥b
简记:线线平行 线面平行
注意:①定理中三个条件缺一不可
②简记:线面平行,则线线平行
③定理的作用:判断直线与直线平行的重要依据
④定理的关键:寻找平面与平面的交线
【例1】如右图的一块木料中,棱BC平行面A'C'
(1)要经过面A'C'内的一点P和棱BC将木料锯开,在木料表面应该怎样画线
(2)所画的线与平面AC是什么位置关系
解:(1)如右图,在平面A'C内,过点P作直线EF,使EF//B'C',并分别
交棱A'B'、D'C' 于点E、F.连接BE、CF,则EF、BE、 CF就是应
画的线
(2) ∵BC∥平面A'C',平面BC'平面A'C'=B'C'
∴BC//B'C'
由(1)知EF//B'C'
∴EF//BC,而BC 平面AC,EF 平面AC
∴EF//平面AC
显然,BE、CF都与平面AC相交
【例2】如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.
证明:连接MO
∵四边形ABCD是平行四边形
∴O是AC的中点
又∵M是PC的中点
∴AP∥OM
又∵AP 平面BDM
OM 平面BDM
∴AP∥平面BDM
又∵AP 平面APGH,平面APGH∩平面BDM=GH
∴AP∥GH
【例3】如图,在三棱柱中,点分别是棱上的点,点是线段上的动点,.若平面,试判断点的位置
解:是的中点
因为平面平面
平面平面
所以
所以四边形是平行四边形
所以
而
所以
故是的中位线
所以是的中点时,平面
方法规律:线面平行的性质和判定经常交替使用,也就是通过线线平行得到线面平行,再通过线面平行得线线平
行.利用线面平行的性质定理解题的具体步骤:
(1)确定(或寻找)一条直线平行于一个平面
(2)确定(或寻找)过这条直线且与这个平行平面相交的平面
(3)确定交线
(4)由性质定理得出线线平行的结论
四、课堂练习
P138 练习
1、如图,在五面体EFABCD中,已知四边形ABCD为梯形,AD∥BC,求证:AD∥EF
证明 ∵AD∥BC,AD 平面BCEF,BC 平面BCEF
∴AD∥平面BCEF
∵AD 平面ADEF,平面ADEF∩平面BCEF=EF
∴AD∥EF
2、如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1
证明:取D1B1的中点O,连接OF,OB(图略)
∵F为C1D1的中点
∴OF∥B1C1且OF=B1C1
又BE∥B1C1,BE=B1C1
∴OF∥BE且OF=BE
∴四边形OFEB是平行四边形,∴EF∥BO
∵EF 平面BDD1B1,BO 平面BDD1B1
∴EF∥平面BDD1B1
五、课堂小结
1、直线与平面平行的性质定理
2、证明线与线、线与面的平行关系的一般规律是:“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段
六、课后作业
习题8.5 7、8
七、课后反思
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
