2021-2022学年人教A版(2019)高中数学选择性必修第一册第一章 空间向量与立体几何 综合测评卷(B卷)(Word含答案解析)
文档属性
| 名称 | 2021-2022学年人教A版(2019)高中数学选择性必修第一册第一章 空间向量与立体几何 综合测评卷(B卷)(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 22:21:53 | ||
图片预览



文档简介
第一章 空间向量与立体几何 综合测评卷(B卷)
一、单选题
1.如图所示,正方体的棱长为,,分别为和上的点,且,则与平面的位置关系是( ).
A.斜交 B.平行
C.垂直 D.不能确定
2.若是平面α内的两个向量,则( )
A.α内任一向量(λ,μ∈R)
B.若存在λ,μ∈R使=,则λ=μ=0
C.若不共线,则空间任一向量 (λ,μ∈R)
D.若不共线,则α内任一向量 (λ,μ∈R)
3.若向量,且与的夹角余弦为,则λ等于( )
A. B. C.或 D.2
4.如图所示,在空间四边形中,,点在上,且,为中点,则( )
A. B.
C. D.
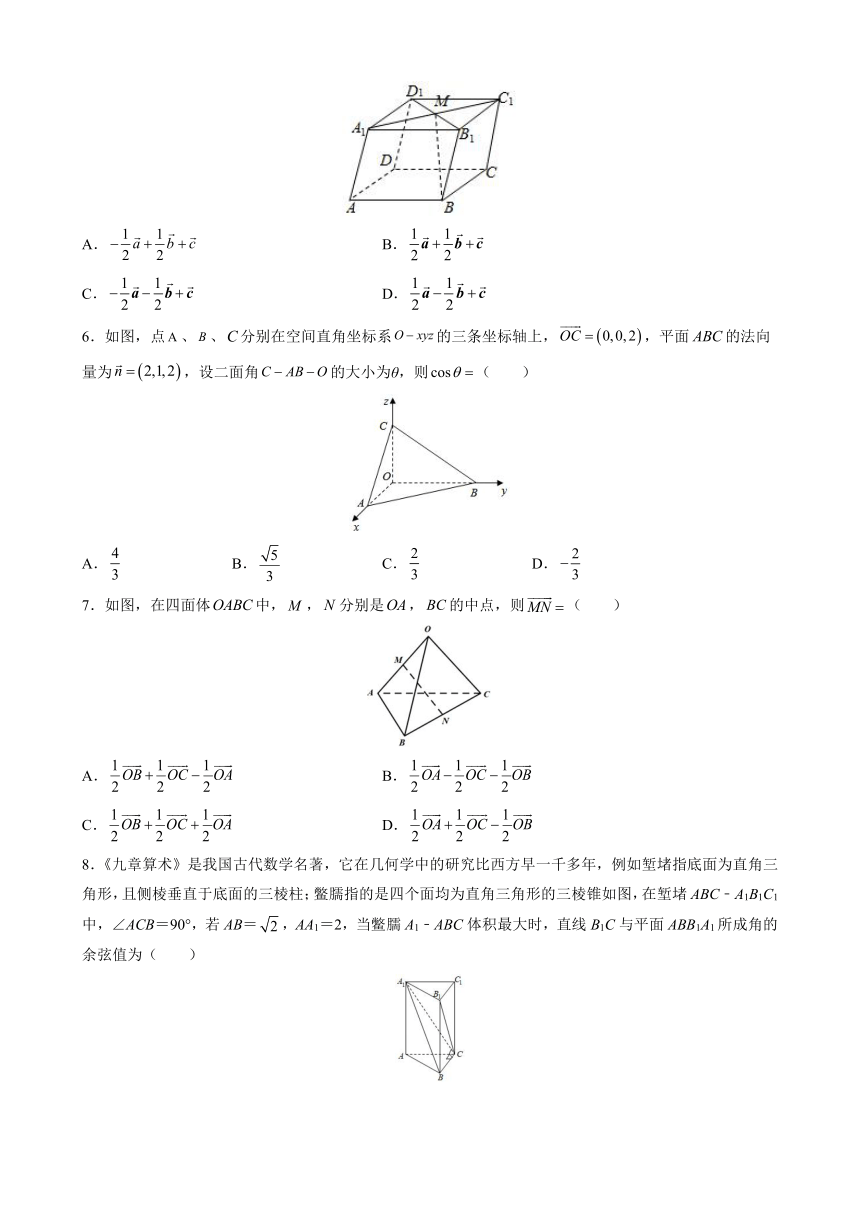
5.如图:在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
6.如图,点、、分别在空间直角坐标系的三条坐标轴上,,平面的法向量为,设二面角的大小为θ,则( )
A. B. C. D.
7.如图,在四面体中,,分别是,的中点,则( )
A. B.
C. D.
8.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;鳖臑指的是四个面均为直角三角形的三棱锥如图,在堑堵ABC﹣A1B1C1中,∠ACB=90°,若AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,直线B1C与平面ABB1A1所成角的余弦值为( )
A. B. C. D.
二、多选题
9.将正方形沿对角线折成直二面角,则下列结论正确的是( )
A.
B.是等边三角形
C.与平面所成的角为90°
D.与所成的角为30°
10.已知分别是三棱锥的棱,的中点,.若异面直线与所成角的大小为60°,则线段的长为( )
A.3 B.6 C. D.
11.如图,在四棱锥中,底面为平行四边形,,,底面,则( )
A.
B.与平面所成角为
C.异面直线与所成角的余弦值为
D.平面与平面所成二面角的平面角为锐角时的余弦值为
12.如图,在长方体,,点为线段上的动点,则下列结论正确的是( )
A.当时,,,三点共线
B.当时,
C.当时,平面
D.当时,平面
三、填空题
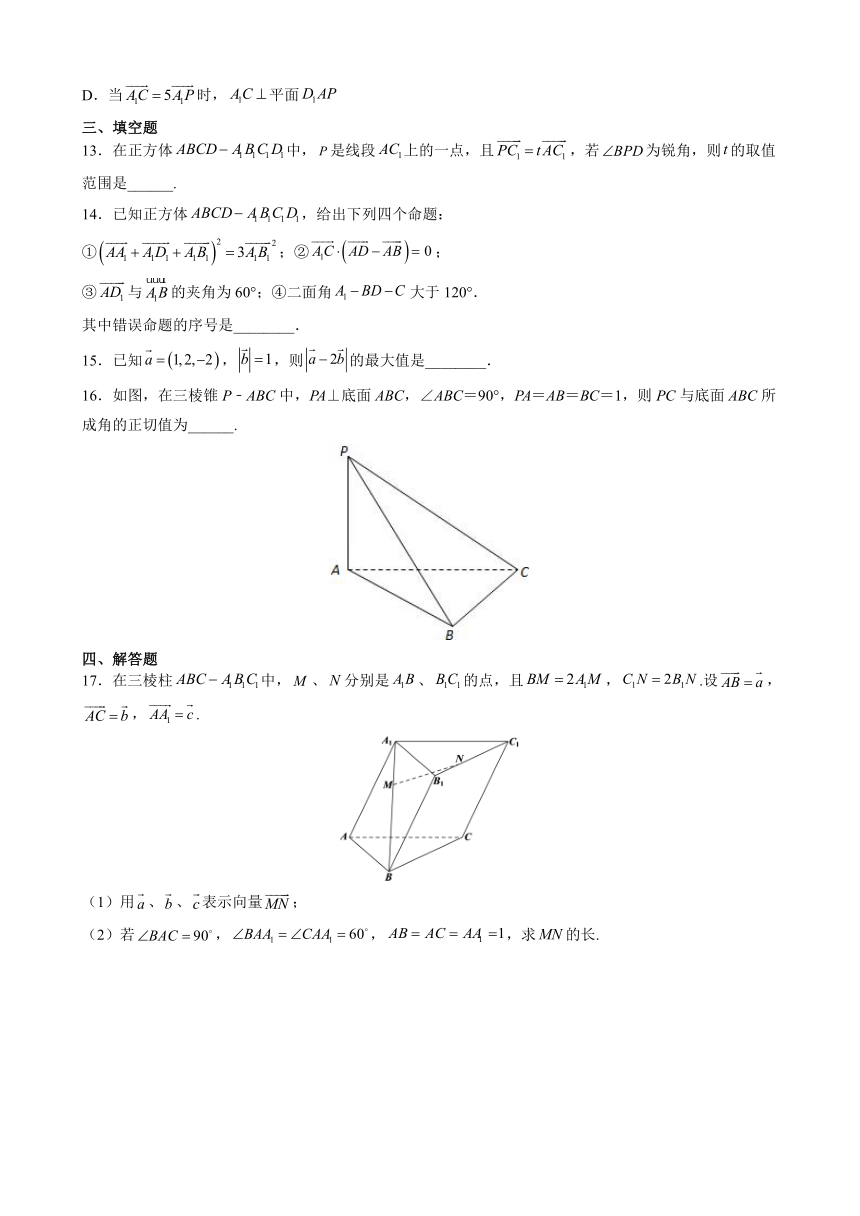
13.在正方体中,是线段上的一点,且,若为锐角,则的取值范围是______.
14.已知正方体,给出下列四个命题:
①;②;
③与的夹角为60°;④二面角大于120°.
其中错误命题的序号是________.
15.已知,,则的最大值是________.
16.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为______.
四、解答题
17.在三棱柱中,、分别是、的点,且,.设,,.
(1)用、、表示向量;
(2)若,,,求的长.
18.如图,在四棱锥S﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面SAD⊥平面ABCD,P为AD的中点,SA=SD=2,BCAD=1,CD.
(Ⅰ)求证:SP⊥AB;
(Ⅱ)求直线BS与平面SCD所成角的正弦值;
(Ⅲ)设M为SC的中点,求二面角S﹣PB﹣M的余弦值.
19.如图,四棱锥的底面是边长为的菱形,,,顶点在底面上的投影为,侧棱与底面所成角的正切值为.
(1)证明:平面;
(2)若点为的中点,求二面角的大小.
20.在四棱锥中,平面平面,是等腰直角三角形,,,,,是的中点,为的中点.
(1)求证:平面;
(2)求二面角的余弦值.
21.在直三棱柱中,,,,分别是,的中点,如图建立空间直角坐标系.
(1)在四边形(包含边界)内找一点,使为等边三角形.
(2)在线段上是否存在一点,使是以为斜边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
22.如图,在三棱锥A﹣BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=,BC=BD=2,∠CBD=90°,E为CD的中点.
(1)求证:AD⊥平面ABC;
(2)求二面角B﹣AE﹣C的余弦值;
(3)已知P是平面ABD内一点,点Q为AE中点,且PQ⊥平面ABE,求线段PQ的长.
参考答案
1.B
【解析】设,,,
由题意知:,又,
,,
则,
与,共面,
平面,又平面平面,平面.
故选:B.
2.D
【解析】当与共线时,A项不正确;当与是相反向量,λ=μ≠0时,=,故B项不正确;
若与不共线,则与、共面的任意向量可以用,表示,对空间向量则不一定,
故C项不正确,D项正确.
故选:D.
3.A
【解析】解:∵向量,
∴,
解得.
故选:A.
4.B
【解析】
故选:B
5.A
【解析】,
,
,
,
故选:A.
6.C
【解析】∵点、、分别在空间直角坐标系的三条坐标轴上,
,平面的法向量为,
二面角的大小为θ,
故选:C.
7.A
【解析】在四面体中,,分别是,的中点,
故选:A.
8.A
【解析】解:在堑堵ABC﹣A1B1C1中,∠ACB=90°,AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,AC=BC=1,
以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
B1(0,1,2),C(0,0,0),A(1,0,0),B(0,1,0),
设平面ABB1A1的法向量,
则,取x=1,得,
设直线B1C与平面ABB1A1所成角为θ,
则,
所以
∴直线B1C与平面ABB1A1所成角的余弦值为.
故选:A.
9.AB
【解析】
对于A选项,如图,取的中点,连接,,,则,,又,平面,又平面,∴,A中结论正确;
对于B选项,由直二面角,得,∴是等边三角形,B中结论正确;
对于C选项,∵平面,∴是与平面所成的角,其大小为45°,C中结论错误;
对于D选项,,不妨设,
则,∴,∴,∴,即与所成的角为60°,D中结论错误.
故选:AB.
10.AD
【解析】如图,取的中点,连接,,.
设与的交角为.因为异面直线与所成的角为60°,所以或,
所以
将,,分别代入上式,得或.
故选:AD.
11.AD
【解析】对于A,由,及余弦定理得,从而,故.由底面,可得.又,所以平面,故.故A正确.
对于B,因为底面,所以就是与平面所成的角,又,所以.故B错误.
对于C,显然是异面直线与所成的角,易得.故C错误.
对于D,以D为原点,,,所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系.
设,则,,,,所以,,.
设平面的一个法向量为,
则,即,
取,则,,
此时.
设平面的一个法向量为,
则,即,
取,则,,此时,
所以,
所以平面与平面所成二面角的平面角为锐角时的余弦值为.故D正确.
故选:AD.
12.ACD
【解析】在长方体中,以点为坐标原点,建立如图所示的空间直角坐标系,
因为,所以,
则,,,,,,,则,.
A选项,当时,为线段的中点,根据长方体的结构特征,为体对角线的中点,因此也为的中点,所以,,三点共线,故A正确.
B选项,当时,,由题意可得,.由,解得,所以,即点为线段上靠近点的五等分点,所以.则,,所以,所以与不垂直,故B错误.
C选项,当时,.
设平面的法向量为,由,令,可得.又,所以,因此,又点不在平面内,所以平面,故C正确.
D选项,当时,,所以,
所以,,因此,.
又,则平面,故D正确.
故选:ACD.
13.
【解析】如下图,建立空间坐标系,
设正方体的边长为,设,
则,
由,得,
,
则,
为锐角,
,
,
则或,
又,
故.
故答案为:.
14.③
【解析】如图,以为坐标原点,分别以所在的直线为轴建立空间直角坐标系,设正方体的棱长为1,则,,
对于①,因为,, 所以,,所以 ,所以①正确,
对于②,因为,所以②正确,
对于③,设与的夹角为,因为,,所以,因为,所以,所以 ③错误,
对于④,设平面的法向量为,则
,令,则,
平面的一个法向量为,
所以,由图可知二面角为钝角,设二面角的平面角为,则,所以,所以④正确,
故答案为:③
15.
【解析】因为,所以,设的夹角为,
,
当时,的最大值是.
故答案为:
16.
【解析】解:底面,
是在底面上的射影,
是与底面所成的角.
,,
,
.即与底面所成角的正切值为.
故答案为:.
17.(1);(2).
【解析】(1)连接,
,由题意可得,
,
所以,;
(2)由已知条件可得,,
因此,.
18.(Ⅰ)证明见解析;(Ⅱ);(Ⅲ).
【解析】(Ⅰ)证明:在△SAD中,∵SA=SD,P为AD的中点,∴SP⊥AD,
∵平面SAD⊥平面ABCD,且平面SAD∩平面ABCD=AD,平面,
∴SP⊥平面ABCD,
又AB 平面ABCD,∴SP⊥AB;
(Ⅱ)解:在直角梯形ABCD中,∵AD∥BC,BC,P为AD中点,
∴BC∥PD,且BC=PD,则四边形BCDP为平行四边形,
∵AD⊥DC,∴AD⊥PB,
由(Ⅰ)可知,SP⊥平面ABCD,故以P为坐标原点,建立空间直角坐标系P﹣xyz,
则P(0,0,0),A(1,0,0),B(0,,0),S(0,0,),C(﹣1,,0),D(﹣1,0,0),
∴(0,,)(0,,0),(﹣1,0,),
设平面SCD的一个法向量,
由,取z=1,得;
设直线BS与平面SCD所成角为α,
则sinα=|cos|.
∴直线BS与平面SCD所成角的正弦值为;
(Ⅲ)解:∵AP⊥SP,AP⊥BP,SP∩BP=P,
∴AP⊥平面SBP,即为平面SPB的一个法向量,
∵M为SC的中点,
∴点M的坐标为(,,),而(0,,0),(,,),
设平面MPB的一个法向量为,
由,取=1,得.
∴cos.
∴二面角S﹣PB﹣M的余弦值为.
19.(1)证明见解析;(2).
【解析】(1)证明:因为四棱锥的底面是边长为的菱形,且,
所以是边长为的等边三角形;
因为,所以三棱锥是正三棱锥,
所以顶点在底面上的投影为为正的中心,故,
又,所以.
因为平面,平面,所以,
而,所以平面.
(2)解:由(1)知,是侧棱与底面所成的角,所以,
而,所以.
建立如图所示的空间直角坐标系,
则,,,,,
故,所以,,,
设平面的法向量为,
则,令,得.
设平面的法向量为,
则,令,得;
,
因为二面角是锐角,所以二面角的大小为.
20.(1)证明见解析;(2).
【解析】(1)证明:取的中点为,连接、、,
因为,,故四边形为等腰梯形,
如图,过作的垂线,垂足分别为,则,
因为,所以,故,同理,
所以,所以.
所以四边形与四边形都是菱形,且为的中点,
所以为的中点,,又因为平面,平面,
所以平面.
(2)解:因为,为的中点,所以;
又因为平面平面,平面平面,
平面,所以平面;
取的中点为,因为为等腰梯形,所以.
以为坐标原点,分别以、、的方向为轴、轴、轴的正方向,建立空间直角坐标系,如图所示:
则,
所以,,.
设平面的一个法向量为,由,得,
取,则,故.
设平面的一个法向量为,由,得,,
取,则,故.
所以,
因为二面角的平面角为锐角,故二面角的余弦值为.
21.(1),2,;(2)存在,,2,.
【解析】(1)直三棱柱中,,,,
故,
若为正三角形,则到的距离为正三角形的高:,
又由在平面内,
故的横纵坐标与中点的横纵坐标相等,竖坐标的绝对值等于正三角形的高,
,,
故中点坐标为,2,,
故点坐标为:,2,;
(2)设点的坐标为,2,,
则,2,,,,,
若为以为斜边的直角三角形,
则,
即,
解得:,或(舍去),
故点的坐标为,2,.
故在线段上存在一点,2,,使是以为斜边的直角三角形.
22.(1)证明见解析;(2);(3).
【解析】(1)因为顶点A在底面BCD上的投影O在棱BD上,
所以AO⊥平面BCD,
因为AO 平面ABD,
所以平面ABD⊥平面BCD,
因为∠CBD=90°,
所以BC⊥BD,
因为平面ABD∩平面BCD=BD,BC 平面BCD,
所以BC⊥平面ABD,
又AD 平面ABD,
所以BC⊥AD,
由AB=AD=,BD=2,得,
所以AD⊥AB,
因为AB∩BC=B,AB 平面ABC,BC 平面ABC,
所以AD⊥平面ABC.
(2)连接OE,因为O为BD的中点,E为CD的中点,OE∥BC,所以OE⊥BD,
如图,以O为坐标原点,分别以OE,OD,OA为x轴,y轴,z轴为正方向,建立空间直角坐标系,
则O(0,0,0),A(0,0,1),B(0,﹣1,0),C(2,﹣1,0),D(0,1,0),E
(1,0,0),
,,,
设平面ABE的一个法向量=(x,y,z),
取x=1,得=(1,﹣1,1),
设平面ACE的一个法向量=(a,b,c),
取c=1,则,
设二面角B﹣AE﹣C的平面角为θ,由图知二面角为锐角,
则cosθ==.
所以二面角B﹣AE﹣C的余弦值为.
(3)设P(0,y,z),Q(,0,),
因为PQ⊥平面ABE,∴.
∴,=λ(1,﹣1,1).
∴ y=,z=0,∴ P(0,,0)
∴ PQ=
一、单选题
1.如图所示,正方体的棱长为,,分别为和上的点,且,则与平面的位置关系是( ).
A.斜交 B.平行
C.垂直 D.不能确定
2.若是平面α内的两个向量,则( )
A.α内任一向量(λ,μ∈R)
B.若存在λ,μ∈R使=,则λ=μ=0
C.若不共线,则空间任一向量 (λ,μ∈R)
D.若不共线,则α内任一向量 (λ,μ∈R)
3.若向量,且与的夹角余弦为,则λ等于( )
A. B. C.或 D.2
4.如图所示,在空间四边形中,,点在上,且,为中点,则( )
A. B.
C. D.
5.如图:在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
6.如图,点、、分别在空间直角坐标系的三条坐标轴上,,平面的法向量为,设二面角的大小为θ,则( )
A. B. C. D.
7.如图,在四面体中,,分别是,的中点,则( )
A. B.
C. D.
8.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;鳖臑指的是四个面均为直角三角形的三棱锥如图,在堑堵ABC﹣A1B1C1中,∠ACB=90°,若AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,直线B1C与平面ABB1A1所成角的余弦值为( )
A. B. C. D.
二、多选题
9.将正方形沿对角线折成直二面角,则下列结论正确的是( )
A.
B.是等边三角形
C.与平面所成的角为90°
D.与所成的角为30°
10.已知分别是三棱锥的棱,的中点,.若异面直线与所成角的大小为60°,则线段的长为( )
A.3 B.6 C. D.
11.如图,在四棱锥中,底面为平行四边形,,,底面,则( )
A.
B.与平面所成角为
C.异面直线与所成角的余弦值为
D.平面与平面所成二面角的平面角为锐角时的余弦值为
12.如图,在长方体,,点为线段上的动点,则下列结论正确的是( )
A.当时,,,三点共线
B.当时,
C.当时,平面
D.当时,平面
三、填空题
13.在正方体中,是线段上的一点,且,若为锐角,则的取值范围是______.
14.已知正方体,给出下列四个命题:
①;②;
③与的夹角为60°;④二面角大于120°.
其中错误命题的序号是________.
15.已知,,则的最大值是________.
16.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为______.
四、解答题
17.在三棱柱中,、分别是、的点,且,.设,,.
(1)用、、表示向量;
(2)若,,,求的长.
18.如图,在四棱锥S﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面SAD⊥平面ABCD,P为AD的中点,SA=SD=2,BCAD=1,CD.
(Ⅰ)求证:SP⊥AB;
(Ⅱ)求直线BS与平面SCD所成角的正弦值;
(Ⅲ)设M为SC的中点,求二面角S﹣PB﹣M的余弦值.
19.如图,四棱锥的底面是边长为的菱形,,,顶点在底面上的投影为,侧棱与底面所成角的正切值为.
(1)证明:平面;
(2)若点为的中点,求二面角的大小.
20.在四棱锥中,平面平面,是等腰直角三角形,,,,,是的中点,为的中点.
(1)求证:平面;
(2)求二面角的余弦值.
21.在直三棱柱中,,,,分别是,的中点,如图建立空间直角坐标系.
(1)在四边形(包含边界)内找一点,使为等边三角形.
(2)在线段上是否存在一点,使是以为斜边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
22.如图,在三棱锥A﹣BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=,BC=BD=2,∠CBD=90°,E为CD的中点.
(1)求证:AD⊥平面ABC;
(2)求二面角B﹣AE﹣C的余弦值;
(3)已知P是平面ABD内一点,点Q为AE中点,且PQ⊥平面ABE,求线段PQ的长.
参考答案
1.B
【解析】设,,,
由题意知:,又,
,,
则,
与,共面,
平面,又平面平面,平面.
故选:B.
2.D
【解析】当与共线时,A项不正确;当与是相反向量,λ=μ≠0时,=,故B项不正确;
若与不共线,则与、共面的任意向量可以用,表示,对空间向量则不一定,
故C项不正确,D项正确.
故选:D.
3.A
【解析】解:∵向量,
∴,
解得.
故选:A.
4.B
【解析】
故选:B
5.A
【解析】,
,
,
,
故选:A.
6.C
【解析】∵点、、分别在空间直角坐标系的三条坐标轴上,
,平面的法向量为,
二面角的大小为θ,
故选:C.
7.A
【解析】在四面体中,,分别是,的中点,
故选:A.
8.A
【解析】解:在堑堵ABC﹣A1B1C1中,∠ACB=90°,AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,AC=BC=1,
以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
B1(0,1,2),C(0,0,0),A(1,0,0),B(0,1,0),
设平面ABB1A1的法向量,
则,取x=1,得,
设直线B1C与平面ABB1A1所成角为θ,
则,
所以
∴直线B1C与平面ABB1A1所成角的余弦值为.
故选:A.
9.AB
【解析】
对于A选项,如图,取的中点,连接,,,则,,又,平面,又平面,∴,A中结论正确;
对于B选项,由直二面角,得,∴是等边三角形,B中结论正确;
对于C选项,∵平面,∴是与平面所成的角,其大小为45°,C中结论错误;
对于D选项,,不妨设,
则,∴,∴,∴,即与所成的角为60°,D中结论错误.
故选:AB.
10.AD
【解析】如图,取的中点,连接,,.
设与的交角为.因为异面直线与所成的角为60°,所以或,
所以
将,,分别代入上式,得或.
故选:AD.
11.AD
【解析】对于A,由,及余弦定理得,从而,故.由底面,可得.又,所以平面,故.故A正确.
对于B,因为底面,所以就是与平面所成的角,又,所以.故B错误.
对于C,显然是异面直线与所成的角,易得.故C错误.
对于D,以D为原点,,,所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系.
设,则,,,,所以,,.
设平面的一个法向量为,
则,即,
取,则,,
此时.
设平面的一个法向量为,
则,即,
取,则,,此时,
所以,
所以平面与平面所成二面角的平面角为锐角时的余弦值为.故D正确.
故选:AD.
12.ACD
【解析】在长方体中,以点为坐标原点,建立如图所示的空间直角坐标系,
因为,所以,
则,,,,,,,则,.
A选项,当时,为线段的中点,根据长方体的结构特征,为体对角线的中点,因此也为的中点,所以,,三点共线,故A正确.
B选项,当时,,由题意可得,.由,解得,所以,即点为线段上靠近点的五等分点,所以.则,,所以,所以与不垂直,故B错误.
C选项,当时,.
设平面的法向量为,由,令,可得.又,所以,因此,又点不在平面内,所以平面,故C正确.
D选项,当时,,所以,
所以,,因此,.
又,则平面,故D正确.
故选:ACD.
13.
【解析】如下图,建立空间坐标系,
设正方体的边长为,设,
则,
由,得,
,
则,
为锐角,
,
,
则或,
又,
故.
故答案为:.
14.③
【解析】如图,以为坐标原点,分别以所在的直线为轴建立空间直角坐标系,设正方体的棱长为1,则,,
对于①,因为,, 所以,,所以 ,所以①正确,
对于②,因为,所以②正确,
对于③,设与的夹角为,因为,,所以,因为,所以,所以 ③错误,
对于④,设平面的法向量为,则
,令,则,
平面的一个法向量为,
所以,由图可知二面角为钝角,设二面角的平面角为,则,所以,所以④正确,
故答案为:③
15.
【解析】因为,所以,设的夹角为,
,
当时,的最大值是.
故答案为:
16.
【解析】解:底面,
是在底面上的射影,
是与底面所成的角.
,,
,
.即与底面所成角的正切值为.
故答案为:.
17.(1);(2).
【解析】(1)连接,
,由题意可得,
,
所以,;
(2)由已知条件可得,,
因此,.
18.(Ⅰ)证明见解析;(Ⅱ);(Ⅲ).
【解析】(Ⅰ)证明:在△SAD中,∵SA=SD,P为AD的中点,∴SP⊥AD,
∵平面SAD⊥平面ABCD,且平面SAD∩平面ABCD=AD,平面,
∴SP⊥平面ABCD,
又AB 平面ABCD,∴SP⊥AB;
(Ⅱ)解:在直角梯形ABCD中,∵AD∥BC,BC,P为AD中点,
∴BC∥PD,且BC=PD,则四边形BCDP为平行四边形,
∵AD⊥DC,∴AD⊥PB,
由(Ⅰ)可知,SP⊥平面ABCD,故以P为坐标原点,建立空间直角坐标系P﹣xyz,
则P(0,0,0),A(1,0,0),B(0,,0),S(0,0,),C(﹣1,,0),D(﹣1,0,0),
∴(0,,)(0,,0),(﹣1,0,),
设平面SCD的一个法向量,
由,取z=1,得;
设直线BS与平面SCD所成角为α,
则sinα=|cos|.
∴直线BS与平面SCD所成角的正弦值为;
(Ⅲ)解:∵AP⊥SP,AP⊥BP,SP∩BP=P,
∴AP⊥平面SBP,即为平面SPB的一个法向量,
∵M为SC的中点,
∴点M的坐标为(,,),而(0,,0),(,,),
设平面MPB的一个法向量为,
由,取=1,得.
∴cos.
∴二面角S﹣PB﹣M的余弦值为.
19.(1)证明见解析;(2).
【解析】(1)证明:因为四棱锥的底面是边长为的菱形,且,
所以是边长为的等边三角形;
因为,所以三棱锥是正三棱锥,
所以顶点在底面上的投影为为正的中心,故,
又,所以.
因为平面,平面,所以,
而,所以平面.
(2)解:由(1)知,是侧棱与底面所成的角,所以,
而,所以.
建立如图所示的空间直角坐标系,
则,,,,,
故,所以,,,
设平面的法向量为,
则,令,得.
设平面的法向量为,
则,令,得;
,
因为二面角是锐角,所以二面角的大小为.
20.(1)证明见解析;(2).
【解析】(1)证明:取的中点为,连接、、,
因为,,故四边形为等腰梯形,
如图,过作的垂线,垂足分别为,则,
因为,所以,故,同理,
所以,所以.
所以四边形与四边形都是菱形,且为的中点,
所以为的中点,,又因为平面,平面,
所以平面.
(2)解:因为,为的中点,所以;
又因为平面平面,平面平面,
平面,所以平面;
取的中点为,因为为等腰梯形,所以.
以为坐标原点,分别以、、的方向为轴、轴、轴的正方向,建立空间直角坐标系,如图所示:
则,
所以,,.
设平面的一个法向量为,由,得,
取,则,故.
设平面的一个法向量为,由,得,,
取,则,故.
所以,
因为二面角的平面角为锐角,故二面角的余弦值为.
21.(1),2,;(2)存在,,2,.
【解析】(1)直三棱柱中,,,,
故,
若为正三角形,则到的距离为正三角形的高:,
又由在平面内,
故的横纵坐标与中点的横纵坐标相等,竖坐标的绝对值等于正三角形的高,
,,
故中点坐标为,2,,
故点坐标为:,2,;
(2)设点的坐标为,2,,
则,2,,,,,
若为以为斜边的直角三角形,
则,
即,
解得:,或(舍去),
故点的坐标为,2,.
故在线段上存在一点,2,,使是以为斜边的直角三角形.
22.(1)证明见解析;(2);(3).
【解析】(1)因为顶点A在底面BCD上的投影O在棱BD上,
所以AO⊥平面BCD,
因为AO 平面ABD,
所以平面ABD⊥平面BCD,
因为∠CBD=90°,
所以BC⊥BD,
因为平面ABD∩平面BCD=BD,BC 平面BCD,
所以BC⊥平面ABD,
又AD 平面ABD,
所以BC⊥AD,
由AB=AD=,BD=2,得,
所以AD⊥AB,
因为AB∩BC=B,AB 平面ABC,BC 平面ABC,
所以AD⊥平面ABC.
(2)连接OE,因为O为BD的中点,E为CD的中点,OE∥BC,所以OE⊥BD,
如图,以O为坐标原点,分别以OE,OD,OA为x轴,y轴,z轴为正方向,建立空间直角坐标系,
则O(0,0,0),A(0,0,1),B(0,﹣1,0),C(2,﹣1,0),D(0,1,0),E
(1,0,0),
,,,
设平面ABE的一个法向量=(x,y,z),
取x=1,得=(1,﹣1,1),
设平面ACE的一个法向量=(a,b,c),
取c=1,则,
设二面角B﹣AE﹣C的平面角为θ,由图知二面角为锐角,
则cosθ==.
所以二面角B﹣AE﹣C的余弦值为.
(3)设P(0,y,z),Q(,0,),
因为PQ⊥平面ABE,∴.
∴,=λ(1,﹣1,1).
∴ y=,z=0,∴ P(0,,0)
∴ PQ=
