2021-2022学年人教版七年级数学上册2.2.3去括号 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册2.2.3去括号 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
给我最大快乐的,
不是已懂的知识,
而是不断的学习.
2.2整式的加减(2)
----去括号
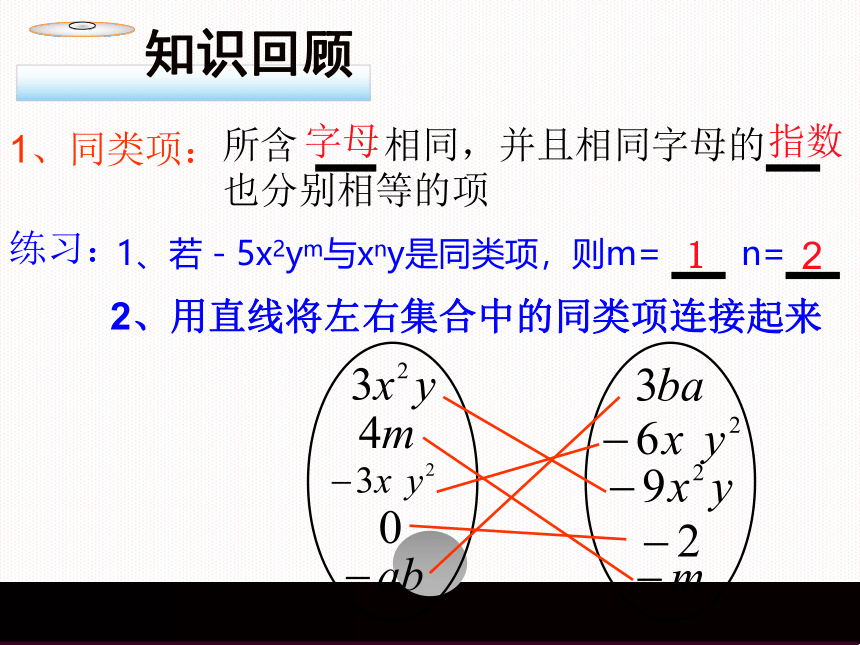
1、同类项:
所含 相同,并且相同字母的 也分别相等的项
练习:
2、用直线将左右集合中的同类项连接起来
知识回顾
1、若-5x2ym与xny是同类项,则m= n=
字母
指数
1
2
2、合并同类项
同类项的 相加
字母和字母的 不变
(1)-3x+2y-5x-7y
= -3x-5x+2y-7y
=(-3-5)x+(2-7)y
= -8x-5y
(2)6x-10x2+12x2-5x
(3)x2y-3xy2+2yx2-y2x
2x2+x
3x2y-4xy2
系数
指数
步骤:
1、找同类项
2、利用加法的交换律
3、乘法的分配律的逆运算
4、合并同类项
学习目标
1.探究去括号法则,并且利用去括号法则将整式化简
2.发现去括号时的符号变化的规律,归纳出去括号法则
3.培养学生观察、分析、归纳问题的能力
温故
化简下列各式
+(+5)=
第1组
第2组
+(-5)=
-(-5)=
-(+5)=
+5
第3组
第4组
+(+7)=
+(+a)=
+(+2m)=
+(+3ab)=
+(-7)=
-(-7)=
-(+7)=
+(-a)=
-(-a)=
-(+a)=
+(-2m)=
-(-2m)=
-(+2m)=
+(-3ab)=
-(-3ab)=
-(+3ab)=
观察看看去括号前后,
各项的符号有什么变化?
+7
+a
+2m
+3ab
-5
+5
-5
-7
+7
-7
-a
+a
-a
-2m
+2m
-2m
-3ab
+3ab
-3ab
探新
化简下列各式
+(+a+b)=
第1组
第2组
+(-5m-n)=
+(-a+b)=
+(+2m-3n)=
-(+a+b)=
-(-a+b)=
-(+2m-3n)=
-(-5m-n)=
观察去括号前后,
猜想括号里各项的符号有什么变化?
+a+b
-a+b
+2m-3n
-5m-n
-a-b
a-b
-2m+3n
5m+n
类比乘法分配律
a(b+c)=ab+ac
讨论和归纳
+(a-b+c)=
-(a-b+c)=
= a-b+c
注意各项的符号和项数
探求
去掉“+( )”,括号内各项的符号不变。
去掉“–( )”,括号内各项的符号改变。
=-a+b-c
= a -3a+7
= -x +3x-2
去括号法则
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
知识点
(5)a + (– b + c ) =
(6) ( a – b ) – ( c + d ) =
( 7 ) – (– a + b ) – c =
( 8 ) – (2x – y ) – ( - x2 + y2 ) =
a-b+c
a-b-c-d
a-b-c
-2x+y+x2-y2
巩固新知
1.口答:去括号
(1)a+(b-c)=
(2)a-(b-c)=
(3)a+(-b+c)=
(4) a-(-b+c)=
a+b-c
a-b+c
a-b+c
a+b-c
为下面的式子去括号
= +(3a-3b+3c)
= 3a-3b+3c
= -6a+3b-12c
= -(3×2a-3b+3×4c)
= +[3(a-b+c)]
= -[3(2a-b+4c)]
(1) +3(a - b+c) (2)- 3(2a - b+4c)
例
= -(6a-3b+12c)
① 2(3a+b)
④ -3(-2a+3b)
=6a+2b
=6a-9b
随堂练习
② 9(x-z)
= 9x- 9z
③4(-a+b-c)
= - 4a+4b- 4c
=-[3 ×(-2a)+3×3b]
=-(-6a+9b)
⑤-3(-b+c)
=-[3×(-b)+3c]
=-(-3b+3c)
⑥-7(-x-y+z)
= - [7(-x)+7(-y)+7z]
= - (-7x-7y+7z)
例题:化简并求值:
(其中a= -2,b=3)
应用提高
解:原式=(2a -2ab)-(2a -3ab )-(-ab)
步骤:
①数乘
=2a -2ab-2a +3ab +ab
②去括号
③找同类项
=(2a -2a )+( -2ab+3ab +ab )
= 2ab
④合并同类项
当a=-2,b=3时
原式= 2×(-2)×3
= -12
⑤代入求值
我能行
3、(5a2-3b2)-5(a2+b2)+3b 其中a=-1,b=1
4、2(a2-ab)-3(2a2-ab)+4a 其中a=-2,b=3
1、2(x2y+xy2)-(x2y+2xy2)其中x=-1,y=2
2、(x+3x2y)-3(x2y-x)-y 其中x=1,y=3
谈谈通过本节课的学习,
你学到了什么?
收获季节
1 去括号的依据是:分配律
2 学习了类比的方法
3 去括号的法则:“-”变 “+”不变
4 去括号在整式加减中的运用
学而不思则罔
思而不学则殆
1. 必做题:P70 3题、4题
2. 选做题:见练习卷
作 业
Homework
给我最大快乐的,
不是已懂的知识,
而是不断的学习.
2.2整式的加减(2)
----去括号
1、同类项:
所含 相同,并且相同字母的 也分别相等的项
练习:
2、用直线将左右集合中的同类项连接起来
知识回顾
1、若-5x2ym与xny是同类项,则m= n=
字母
指数
1
2
2、合并同类项
同类项的 相加
字母和字母的 不变
(1)-3x+2y-5x-7y
= -3x-5x+2y-7y
=(-3-5)x+(2-7)y
= -8x-5y
(2)6x-10x2+12x2-5x
(3)x2y-3xy2+2yx2-y2x
2x2+x
3x2y-4xy2
系数
指数
步骤:
1、找同类项
2、利用加法的交换律
3、乘法的分配律的逆运算
4、合并同类项
学习目标
1.探究去括号法则,并且利用去括号法则将整式化简
2.发现去括号时的符号变化的规律,归纳出去括号法则
3.培养学生观察、分析、归纳问题的能力
温故
化简下列各式
+(+5)=
第1组
第2组
+(-5)=
-(-5)=
-(+5)=
+5
第3组
第4组
+(+7)=
+(+a)=
+(+2m)=
+(+3ab)=
+(-7)=
-(-7)=
-(+7)=
+(-a)=
-(-a)=
-(+a)=
+(-2m)=
-(-2m)=
-(+2m)=
+(-3ab)=
-(-3ab)=
-(+3ab)=
观察看看去括号前后,
各项的符号有什么变化?
+7
+a
+2m
+3ab
-5
+5
-5
-7
+7
-7
-a
+a
-a
-2m
+2m
-2m
-3ab
+3ab
-3ab
探新
化简下列各式
+(+a+b)=
第1组
第2组
+(-5m-n)=
+(-a+b)=
+(+2m-3n)=
-(+a+b)=
-(-a+b)=
-(+2m-3n)=
-(-5m-n)=
观察去括号前后,
猜想括号里各项的符号有什么变化?
+a+b
-a+b
+2m-3n
-5m-n
-a-b
a-b
-2m+3n
5m+n
类比乘法分配律
a(b+c)=ab+ac
讨论和归纳
+(a-b+c)=
-(a-b+c)=
= a-b+c
注意各项的符号和项数
探求
去掉“+( )”,括号内各项的符号不变。
去掉“–( )”,括号内各项的符号改变。
=-a+b-c
= a -3a+7
= -x +3x-2
去括号法则
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
知识点
(5)a + (– b + c ) =
(6) ( a – b ) – ( c + d ) =
( 7 ) – (– a + b ) – c =
( 8 ) – (2x – y ) – ( - x2 + y2 ) =
a-b+c
a-b-c-d
a-b-c
-2x+y+x2-y2
巩固新知
1.口答:去括号
(1)a+(b-c)=
(2)a-(b-c)=
(3)a+(-b+c)=
(4) a-(-b+c)=
a+b-c
a-b+c
a-b+c
a+b-c
为下面的式子去括号
= +(3a-3b+3c)
= 3a-3b+3c
= -6a+3b-12c
= -(3×2a-3b+3×4c)
= +[3(a-b+c)]
= -[3(2a-b+4c)]
(1) +3(a - b+c) (2)- 3(2a - b+4c)
例
= -(6a-3b+12c)
① 2(3a+b)
④ -3(-2a+3b)
=6a+2b
=6a-9b
随堂练习
② 9(x-z)
= 9x- 9z
③4(-a+b-c)
= - 4a+4b- 4c
=-[3 ×(-2a)+3×3b]
=-(-6a+9b)
⑤-3(-b+c)
=-[3×(-b)+3c]
=-(-3b+3c)
⑥-7(-x-y+z)
= - [7(-x)+7(-y)+7z]
= - (-7x-7y+7z)
例题:化简并求值:
(其中a= -2,b=3)
应用提高
解:原式=(2a -2ab)-(2a -3ab )-(-ab)
步骤:
①数乘
=2a -2ab-2a +3ab +ab
②去括号
③找同类项
=(2a -2a )+( -2ab+3ab +ab )
= 2ab
④合并同类项
当a=-2,b=3时
原式= 2×(-2)×3
= -12
⑤代入求值
我能行
3、(5a2-3b2)-5(a2+b2)+3b 其中a=-1,b=1
4、2(a2-ab)-3(2a2-ab)+4a 其中a=-2,b=3
1、2(x2y+xy2)-(x2y+2xy2)其中x=-1,y=2
2、(x+3x2y)-3(x2y-x)-y 其中x=1,y=3
谈谈通过本节课的学习,
你学到了什么?
收获季节
1 去括号的依据是:分配律
2 学习了类比的方法
3 去括号的法则:“-”变 “+”不变
4 去括号在整式加减中的运用
学而不思则罔
思而不学则殆
1. 必做题:P70 3题、4题
2. 选做题:见练习卷
作 业
Homework
