2021-2022学年度北师大版八年级数学上册课件: 第一章 勾股定理 几何体中最短路径问题(26张)
文档属性
| 名称 | 2021-2022学年度北师大版八年级数学上册课件: 第一章 勾股定理 几何体中最短路径问题(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 712.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:24:21 | ||
图片预览






文档简介
(共26张PPT)
专 题 复 习
几何体中最短路径问题
学习目标
1.探索、发现立体图形展开成平面图形的各种途径,运用勾股定
理求最短路径问题.(重点)
2.利用数学中的建模思想构造直角三角形,寻找不同路径,运用
勾股定理,解决实际问题.(难点)
知识回顾
1.勾股定理:直角三角形两直角边的平方和等于 ,如果
用a,b,c分别表示直角三角形的直角边和斜边,那么 .
2.几何体中的最短路径问题是将立体图形展开成一个 面图形,再
利用平面上:两点之间, ,构造 ,解决最
短路径问题.
立体图形 → 平面图形 → 直角三角形问题
斜边的平方
a +b =c
平
线段最短
直角三角形
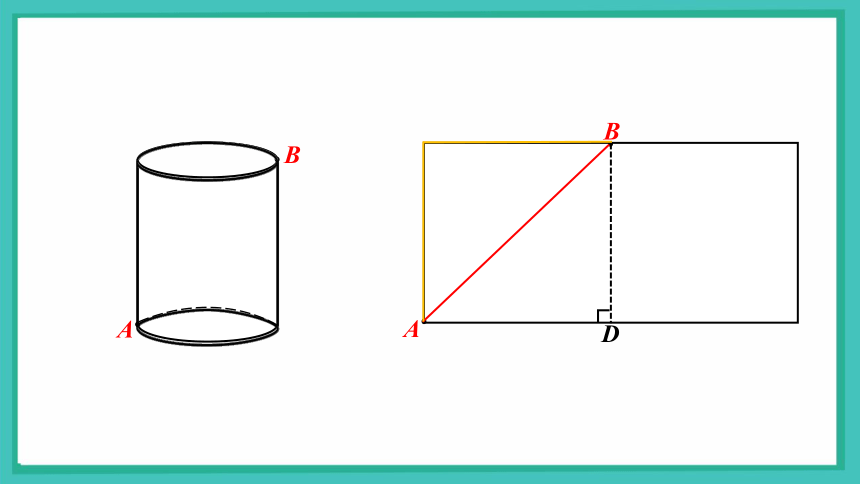
在圆柱形玻璃杯上一点B处有一滴蜂蜜,此时两只蚂蚁正好在杯外壁A处,两只蚂蚁都想品尝美味的蜂蜜,它们决定比赛,路线自选,看谁先到达B处,假设它们的速度相同,该如何选择路径,赢得比赛的胜利呢?
情境引入
B
A
蚂蚁在圆柱体上的路径
A
B
A
B
D
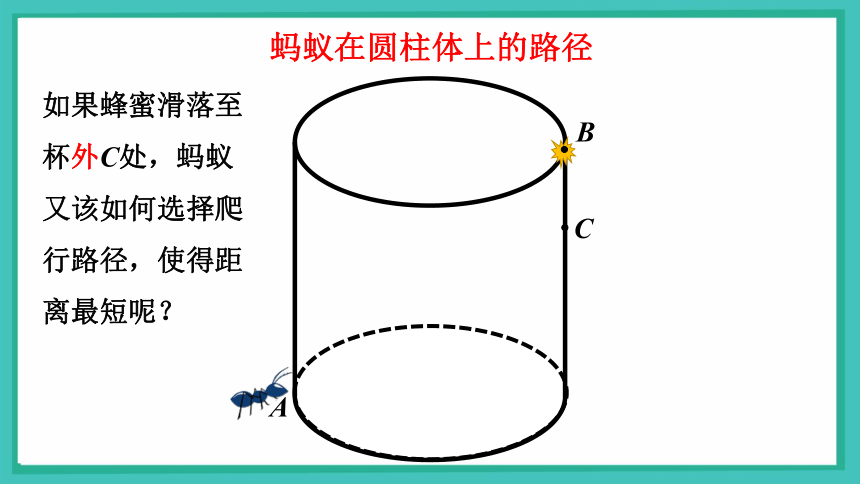
蚂蚁在圆柱体上的路径
C
B
A
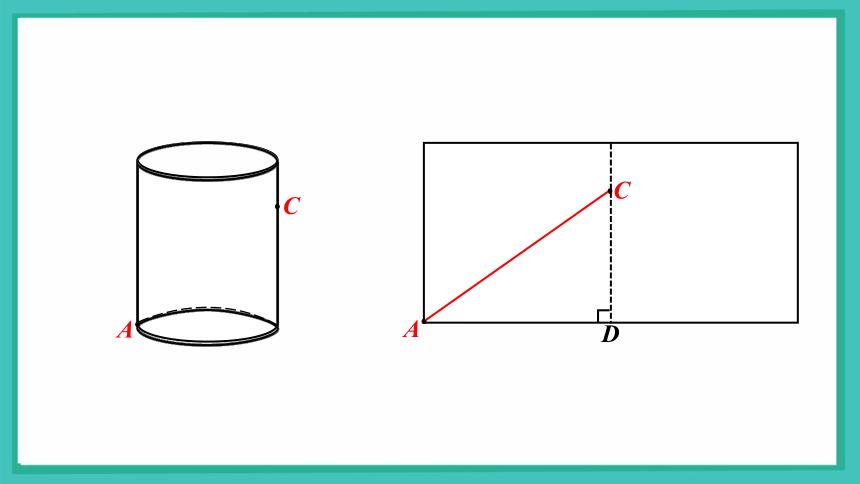
如果蜂蜜滑落至杯外C处,蚂蚁又该如何选择爬行路径,使得距离最短呢?
A
C
A
C
D
类型1 圆柱体中的最短路径问题
母题1.如图,若圆柱的底面周长是40cm,高是30cm,一只蚂蚁从圆柱底部
A处沿侧面爬行一圈到达顶部B处,则这只蚂蚁爬行的距离是( )
A.80cm B.70cm C.60cm D.50cm
解析:
A
B
C
∵圆柱的底面周长是40cm,高是30cm,
∴在Rt△ABC中,
AB = AC + BC =40 +30 =2500.
∴AB=50cm.
D
典例分析
B
A
圆柱体中的最短路径问题
h
h
2πr
r
归纳
数学思想:
转化思想
变式1.如图,已知圆柱底面的周长为24dm,圆柱高为5dm,在圆柱的
侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最
小为 .
解析:
∵圆柱底面的周长为24dm,圆柱高为5dm,
∴AB=5dm,BC=12dm.
∴在Rt△ABC中,由勾股定理得
AC =12 +5 =169.
∴AC=13dm.
∴这圈金属丝的周长最小为2AC=26dm.
26dm
A
B
C
A '
A
B
C
A
C
如果蜂蜜滑落至杯内C处呢?
E
H
F
G
N
M
C
Q
A
A'
P
变式2.如图,圆柱形玻璃杯高为12cm,底面周长为18cm,在杯内离杯底
4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
解析:
∵AE=A'E,A'P=AP,
∴AP+PC=A'P+PC=A'C.
∵CQ= ×18=9cm,A'Q=12-4+4=12cm,
在Rt△A'QC中,A'C= =15cm .
15
A
C
类型2 台阶中的最短路径问题
母题2.如图,台阶阶梯每一层高2dm,宽4dm,长5dm.
一只蚂蚁在A点,有个小甜品在B点,蚂蚁想品
尝美味的甜品,它爬行的最短路程是 .
解析:
13dm
A
5
C
B
2
4
2
4
如图所示,
∵它的每一级的长宽高为2dm,宽4dm,长5dm,
∴在Rt△ABC中,AB= =13dm.
a
b
c
a
b
c
b
c
b
c
归纳
台阶中的最短路径问题
变式.如图所示,ABCD是长方形地面,长AB=20m,宽AD=10m.
中间竖有一堵砖墙高MN=2m.一只蚂蚁从A点爬到C点,它
必须翻过中间那堵墙,则它至少要走 m的路程.
解析:如图所示,将图展开,图形长度增加2MN,
原图长度增加4m,则AB=20+4=24m,
连接AC,
∵在Rt△ABC中,AB=24m,AD=10m
∴
∴蚂蚁从A点爬到C点,至少要走26m的路程.
26
A
D
B
C
N
M
A
B
D
C
M
N
类型3 长方体中的最短路径问题
母题3.如图,现有一长方体的实心木块,有一蚂蚁从A处出发
沿长方体表面爬行到C'处,若长方体的长AD=2cm,
宽AA'=1cm,高AB=4cm,则蚂蚁爬行的最短路径长
是多少cm?
长
宽
高
长方体中的最短路径问题
归纳
长
长
高
高
宽
宽
数学思想:
分类讨论思想
找方法、巧归纳
1.展:利用“ 思想”将 图形转化成 图形;
转化
立体
平面
2.找:在 展开图中,找到两点所在的位置,运用两点之
间, ,构建 并应用 定理解决问题;
平面
线段最短
直角三角形
勾股
3.算:利用“ ”进行分类讨论,算出最 路径。
分类讨论思想
短
小结
作业
必做题:课本P15 第4题
选做题:思考题
脚
踏
实
地
不
言
弃
巧施智慧得成功
谢 谢 大 家
再 见 !
思考题.如图,长方体盒子的长为15cm,宽为10cm,高为20cm,
点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A
到点B.蚂蚁爬行的最短距离是多少cm?
∵长方体的宽为10cm,高为20cm,点B离点C为5cm,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在Rt△ABD中,根据勾股定理得:
∴
同理可得,
同理可得,
解:
把长方体的右侧表面剪开与前面所在的平面形成一个长方形,如图1:
把长方体的右侧表面剪开与上面所在的平面形成一个长方形,如图2:
把长方体的上表面剪开与后面所在的平面形成一个长方形,如图3:
∴蚂蚁爬行的最短距离是25cm
∵
专 题 复 习
几何体中最短路径问题
学习目标
1.探索、发现立体图形展开成平面图形的各种途径,运用勾股定
理求最短路径问题.(重点)
2.利用数学中的建模思想构造直角三角形,寻找不同路径,运用
勾股定理,解决实际问题.(难点)
知识回顾
1.勾股定理:直角三角形两直角边的平方和等于 ,如果
用a,b,c分别表示直角三角形的直角边和斜边,那么 .
2.几何体中的最短路径问题是将立体图形展开成一个 面图形,再
利用平面上:两点之间, ,构造 ,解决最
短路径问题.
立体图形 → 平面图形 → 直角三角形问题
斜边的平方
a +b =c
平
线段最短
直角三角形
在圆柱形玻璃杯上一点B处有一滴蜂蜜,此时两只蚂蚁正好在杯外壁A处,两只蚂蚁都想品尝美味的蜂蜜,它们决定比赛,路线自选,看谁先到达B处,假设它们的速度相同,该如何选择路径,赢得比赛的胜利呢?
情境引入
B
A
蚂蚁在圆柱体上的路径
A
B
A
B
D
蚂蚁在圆柱体上的路径
C
B
A
如果蜂蜜滑落至杯外C处,蚂蚁又该如何选择爬行路径,使得距离最短呢?
A
C
A
C
D
类型1 圆柱体中的最短路径问题
母题1.如图,若圆柱的底面周长是40cm,高是30cm,一只蚂蚁从圆柱底部
A处沿侧面爬行一圈到达顶部B处,则这只蚂蚁爬行的距离是( )
A.80cm B.70cm C.60cm D.50cm
解析:
A
B
C
∵圆柱的底面周长是40cm,高是30cm,
∴在Rt△ABC中,
AB = AC + BC =40 +30 =2500.
∴AB=50cm.
D
典例分析
B
A
圆柱体中的最短路径问题
h
h
2πr
r
归纳
数学思想:
转化思想
变式1.如图,已知圆柱底面的周长为24dm,圆柱高为5dm,在圆柱的
侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最
小为 .
解析:
∵圆柱底面的周长为24dm,圆柱高为5dm,
∴AB=5dm,BC=12dm.
∴在Rt△ABC中,由勾股定理得
AC =12 +5 =169.
∴AC=13dm.
∴这圈金属丝的周长最小为2AC=26dm.
26dm
A
B
C
A '
A
B
C
A
C
如果蜂蜜滑落至杯内C处呢?
E
H
F
G
N
M
C
Q
A
A'
P
变式2.如图,圆柱形玻璃杯高为12cm,底面周长为18cm,在杯内离杯底
4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
解析:
∵AE=A'E,A'P=AP,
∴AP+PC=A'P+PC=A'C.
∵CQ= ×18=9cm,A'Q=12-4+4=12cm,
在Rt△A'QC中,A'C= =15cm .
15
A
C
类型2 台阶中的最短路径问题
母题2.如图,台阶阶梯每一层高2dm,宽4dm,长5dm.
一只蚂蚁在A点,有个小甜品在B点,蚂蚁想品
尝美味的甜品,它爬行的最短路程是 .
解析:
13dm
A
5
C
B
2
4
2
4
如图所示,
∵它的每一级的长宽高为2dm,宽4dm,长5dm,
∴在Rt△ABC中,AB= =13dm.
a
b
c
a
b
c
b
c
b
c
归纳
台阶中的最短路径问题
变式.如图所示,ABCD是长方形地面,长AB=20m,宽AD=10m.
中间竖有一堵砖墙高MN=2m.一只蚂蚁从A点爬到C点,它
必须翻过中间那堵墙,则它至少要走 m的路程.
解析:如图所示,将图展开,图形长度增加2MN,
原图长度增加4m,则AB=20+4=24m,
连接AC,
∵在Rt△ABC中,AB=24m,AD=10m
∴
∴蚂蚁从A点爬到C点,至少要走26m的路程.
26
A
D
B
C
N
M
A
B
D
C
M
N
类型3 长方体中的最短路径问题
母题3.如图,现有一长方体的实心木块,有一蚂蚁从A处出发
沿长方体表面爬行到C'处,若长方体的长AD=2cm,
宽AA'=1cm,高AB=4cm,则蚂蚁爬行的最短路径长
是多少cm?
长
宽
高
长方体中的最短路径问题
归纳
长
长
高
高
宽
宽
数学思想:
分类讨论思想
找方法、巧归纳
1.展:利用“ 思想”将 图形转化成 图形;
转化
立体
平面
2.找:在 展开图中,找到两点所在的位置,运用两点之
间, ,构建 并应用 定理解决问题;
平面
线段最短
直角三角形
勾股
3.算:利用“ ”进行分类讨论,算出最 路径。
分类讨论思想
短
小结
作业
必做题:课本P15 第4题
选做题:思考题
脚
踏
实
地
不
言
弃
巧施智慧得成功
谢 谢 大 家
再 见 !
思考题.如图,长方体盒子的长为15cm,宽为10cm,高为20cm,
点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A
到点B.蚂蚁爬行的最短距离是多少cm?
∵长方体的宽为10cm,高为20cm,点B离点C为5cm,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在Rt△ABD中,根据勾股定理得:
∴
同理可得,
同理可得,
解:
把长方体的右侧表面剪开与前面所在的平面形成一个长方形,如图1:
把长方体的右侧表面剪开与上面所在的平面形成一个长方形,如图2:
把长方体的上表面剪开与后面所在的平面形成一个长方形,如图3:
∴蚂蚁爬行的最短距离是25cm
∵
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
