2021-2022学年度人教版九年级数学上册课件 : 21.3 第1课时 传播问题与一元二次方程(16张)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学上册课件 : 21.3 第1课时 传播问题与一元二次方程(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:35:57 | ||
图片预览






文档简介
(共16张PPT)
RJ九(上)
教学课件
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第1课时 传播问题与一元二次方程
学习目标
1.会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(传播问题)中的数量关系.(难点)
3.会找出实际问题(传播问题等)中的相等关系并建模解决问题.
传染病,一传十,
十传百… …
问题1: 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
合作探究:
传播问题与一元二次方
第2轮
小明
1
2
x
第1轮
第1轮传染后人数:x+1
小明
第2轮传染后人数:x(x+1)
注意:不要忽视小明的二次传染
x1= , x2= .
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.根据题意,得
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
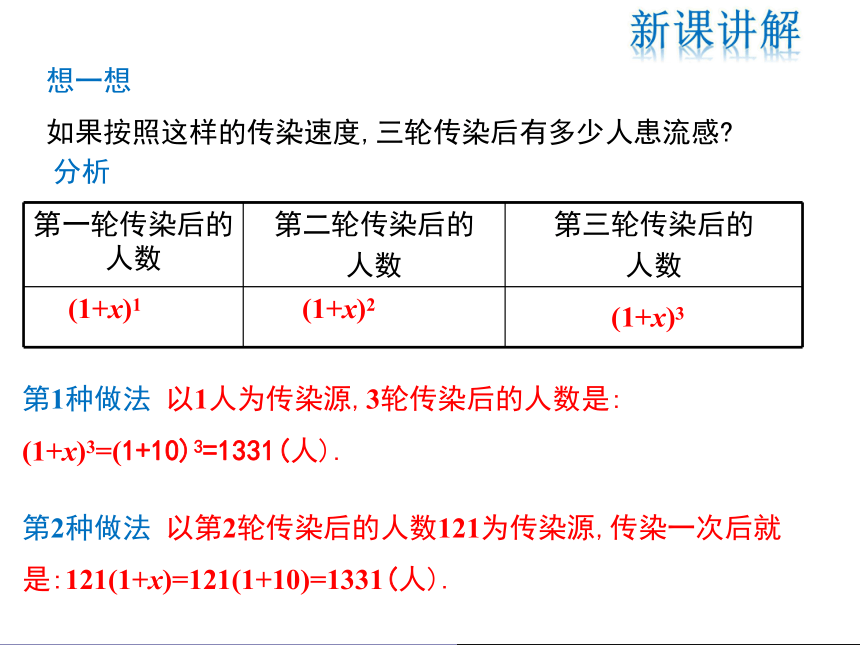
想一想
如果按照这样的传染速度,三轮传染后有多少人患流感
第2种做法 以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331(人).
第一轮传染后的人数 第二轮传染后的
人数 第三轮传染后的
人数
(1+x)1 (1+x)2
分析
第1种做法 以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331(人).
(1+x)3
1.列一元二次方程解应用题时,要注意应用题的内在数量关系,选择适当的条件列代数式,选择剩下的一个关系列方程.
2.在解出方程后要注意检验结果符不符合题意或实际情况,要把不符合实际情况的方程的根舍去.
某种电脑病毒传播速度非常快,如果一台电脑被感染,
经过两轮感染后就会有 100 台电脑被感染.请你用学过的知识
分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不
到有效控制,4 轮感染后,被感染的电脑会不会超过 7000 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑,则
1+x+x(1+x)=100,即(1+x)2=100.
解得 x1=9,x2=-11(舍去).∴x=9.
4 轮感染后,被感染的电脑数为(1+x)4=104>7000.
答:每轮感染中平均每一台电脑会感染 9 台电脑,4 轮感染后,被感染的电脑会超过 7000 台.
例题
例题
1.中秋将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A. x2=1980 B. x(x+1)=1980
C. x(x-1)=1980 D. x(x-1)=1980
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)2=73
D
B
3.一个两位数,十位上的数字与个位上的数字之和为5,把这个数的个位数字与十位数字对调后,所得的新数与原数的积为736,求原数.
解:设原数个位上的数字为x,十位上的数字为(5-x),则原数表示为[10(5-x)+x],对调后新数表示为[10x+(5-x)]. 根据题意列方程,得
[10(5-x)+x] [10x+(5-x)]=736.
化简整理,得
x2-5x+6=0,
解得
x1=3,x2=2.
所以这个两位数是32或23.
4.甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
解:设每天平均一个人传染了x人.根据题意,得
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,再经过5天的传染后,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
故9(1+x)5=9(1+2)5=2187,
或(1+x)7= (1+2)7=2187.
5.要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排15场比赛,应邀请多少个球队参加比赛
答:应邀请6支球队参赛.
解:设应邀请x支球队参赛.由题意可列方程
化简,得
x2-x=30,
解得
x1=-5 (舍去),x2=6.
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同.不同的地方是要检验根的合理性
传播问题
数量关系:
第一轮传播后的量=传播前的量× (1+传播速度)
第二轮传播后的量=第一轮传播后的量× (1+传播速度)=传播前的量× (1+传播速度)2
数字问题
握手问题
送照片问题
关键要设数位上的数字,要准确地表示出原数
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲送乙照片与乙送甲照片是要两张照片,故总数不要除以2
步骤
类型
RJ九(上)
教学课件
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第1课时 传播问题与一元二次方程
学习目标
1.会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(传播问题)中的数量关系.(难点)
3.会找出实际问题(传播问题等)中的相等关系并建模解决问题.
传染病,一传十,
十传百… …
问题1: 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
合作探究:
传播问题与一元二次方
第2轮
小明
1
2
x
第1轮
第1轮传染后人数:x+1
小明
第2轮传染后人数:x(x+1)
注意:不要忽视小明的二次传染
x1= , x2= .
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.根据题意,得
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
想一想
如果按照这样的传染速度,三轮传染后有多少人患流感
第2种做法 以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331(人).
第一轮传染后的人数 第二轮传染后的
人数 第三轮传染后的
人数
(1+x)1 (1+x)2
分析
第1种做法 以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331(人).
(1+x)3
1.列一元二次方程解应用题时,要注意应用题的内在数量关系,选择适当的条件列代数式,选择剩下的一个关系列方程.
2.在解出方程后要注意检验结果符不符合题意或实际情况,要把不符合实际情况的方程的根舍去.
某种电脑病毒传播速度非常快,如果一台电脑被感染,
经过两轮感染后就会有 100 台电脑被感染.请你用学过的知识
分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不
到有效控制,4 轮感染后,被感染的电脑会不会超过 7000 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑,则
1+x+x(1+x)=100,即(1+x)2=100.
解得 x1=9,x2=-11(舍去).∴x=9.
4 轮感染后,被感染的电脑数为(1+x)4=104>7000.
答:每轮感染中平均每一台电脑会感染 9 台电脑,4 轮感染后,被感染的电脑会超过 7000 台.
例题
例题
1.中秋将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A. x2=1980 B. x(x+1)=1980
C. x(x-1)=1980 D. x(x-1)=1980
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)2=73
D
B
3.一个两位数,十位上的数字与个位上的数字之和为5,把这个数的个位数字与十位数字对调后,所得的新数与原数的积为736,求原数.
解:设原数个位上的数字为x,十位上的数字为(5-x),则原数表示为[10(5-x)+x],对调后新数表示为[10x+(5-x)]. 根据题意列方程,得
[10(5-x)+x] [10x+(5-x)]=736.
化简整理,得
x2-5x+6=0,
解得
x1=3,x2=2.
所以这个两位数是32或23.
4.甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
解:设每天平均一个人传染了x人.根据题意,得
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,再经过5天的传染后,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
故9(1+x)5=9(1+2)5=2187,
或(1+x)7= (1+2)7=2187.
5.要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排15场比赛,应邀请多少个球队参加比赛
答:应邀请6支球队参赛.
解:设应邀请x支球队参赛.由题意可列方程
化简,得
x2-x=30,
解得
x1=-5 (舍去),x2=6.
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同.不同的地方是要检验根的合理性
传播问题
数量关系:
第一轮传播后的量=传播前的量× (1+传播速度)
第二轮传播后的量=第一轮传播后的量× (1+传播速度)=传播前的量× (1+传播速度)2
数字问题
握手问题
送照片问题
关键要设数位上的数字,要准确地表示出原数
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲送乙照片与乙送甲照片是要两张照片,故总数不要除以2
步骤
类型
同课章节目录
