第三章 勾股定理单元训练 2021-2022学年苏科版八年级上学期数学(Word版含答案)
文档属性
| 名称 | 第三章 勾股定理单元训练 2021-2022学年苏科版八年级上学期数学(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:40:41 | ||
图片预览


文档简介
第三章勾股定理单元基础靶向训练
一、选择题(本大题共8小题,共24.0分)
若直角三角形两直角边长分别为和,则斜边的长为
A. B. C. D.
如图,在中,,,,于,则的长是
A. B. C. D.
如图,分别以直角三边为边向外作三个正方形,其面积分别用、、表示,若,,那么
A. B. C. D.
如图,正方形小方格的边长为,则网格中的是
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上答案都不对
下列四组数:,,,,,,,,其中是勾股数的有
A. 组 B. 组 C. 组 D. 组
下列条件中,不能判定是直角三角形的是
A. B. ::::
C. D. ::::
要从电线杆上离地面处向地面拉一根长的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A. B. C. D.
我国南宋著名数学家秦九韶的著作数书九章里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,问这块沙田面积有多大?题中“里”是我国市制长度单位,里米,则该沙田的面积为
A. 平方千米 B. 平方千米 C. 平方千米 D. 平方千米
二、填空题(本大题共8小题,共32.0分)
如果等腰三角形的腰长为,底边长为,那么它的面积为_________.
如图是“俄罗斯方块”游戏中的一个图案,由四个完全相同的小正方形拼成,则的度数为________.
已知直角三角形的两边长分别为和,则第三边长为_____________.
九章算术是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长,如果设,则可列方程为______.
若的三边,,满足,则的形状为________________.
若一个直角三角形的一条直角边长是,另一条直角边比斜边短,斜边的长是______.
将勾股数,,扩大倍,倍,倍,,可以得到勾股数,,;,,;,,;,则我们把,,这样的勾股数称为基本勾股数,请你也写出三组基本勾股数______,______,______.
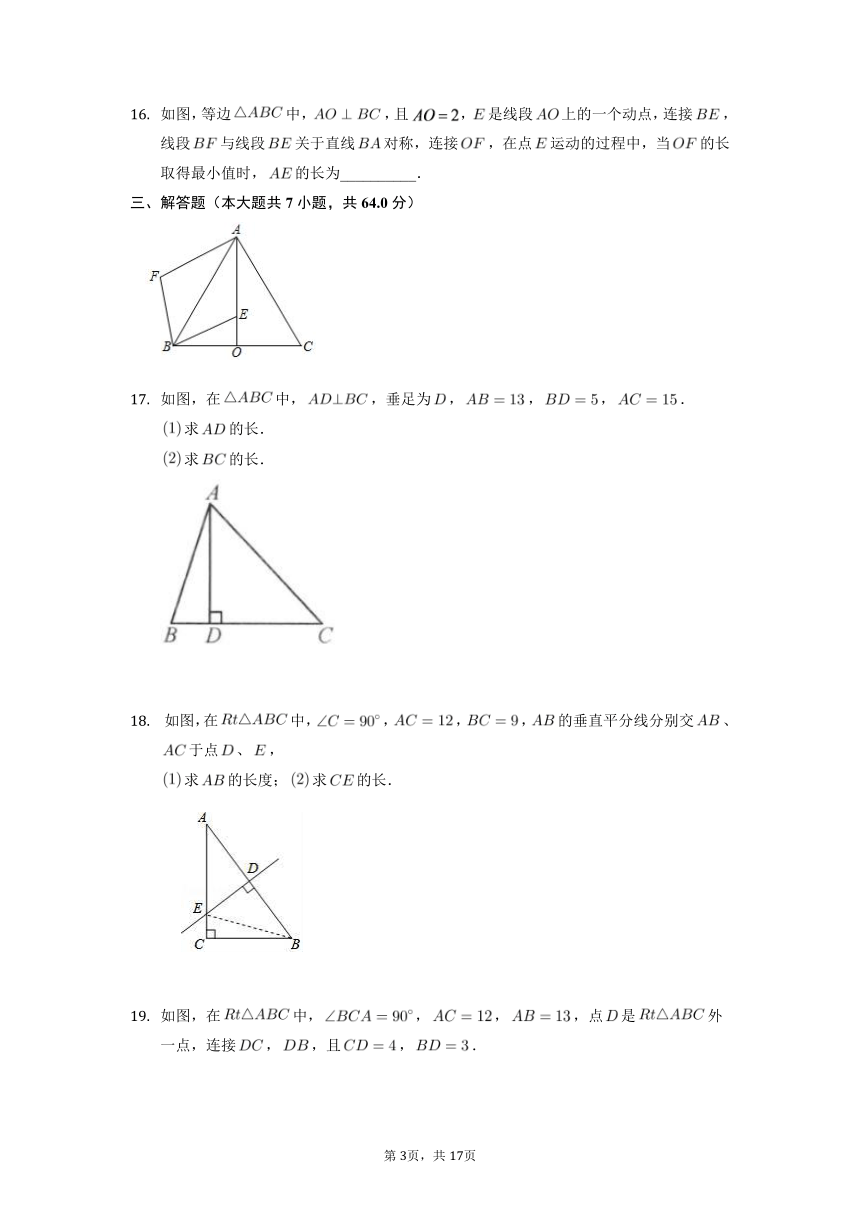
如图,等边中,,且,是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点运动的过程中,当的长取得最小值时,的长为__________.
三、解答题(本大题共7小题,共64.0分)
如图,在中,,垂足为,,,.
求的长.
求的长.
如图,在中,,,,的垂直平分线分别交、于点、,
求的长度;求的长.
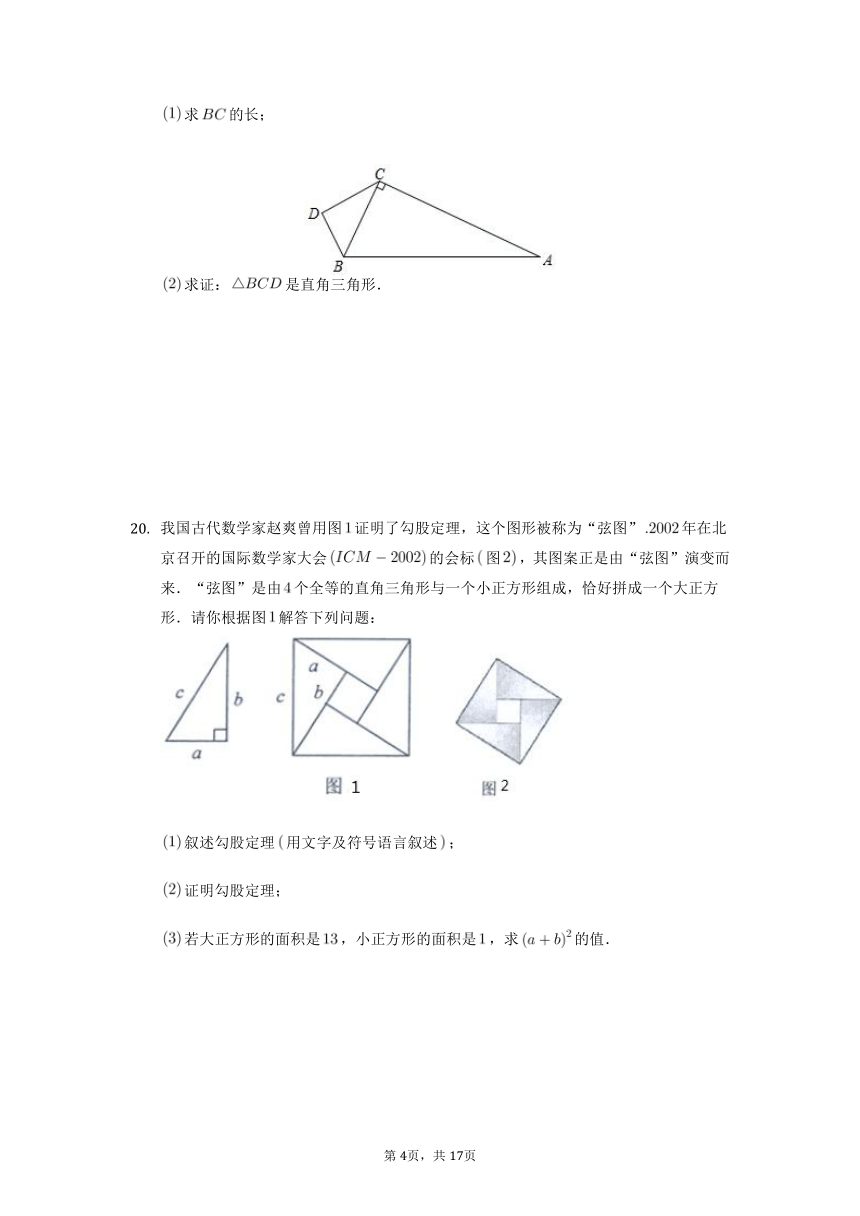
如图,在中,,,,点是外一点,连接,,且,.
求的长;
求证:是直角三角形.
我国古代数学家赵爽曾用图证明了勾股定理,这个图形被称为“弦图”年在北京召开的国际数学家大会的会标图,其图案正是由“弦图”演变而来.“弦图”是由个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.请你根据图解答下列问题:
叙述勾股定理用文字及符号语言叙述;
证明勾股定理;
若大正方形的面积是,小正方形的面积是,求的值.
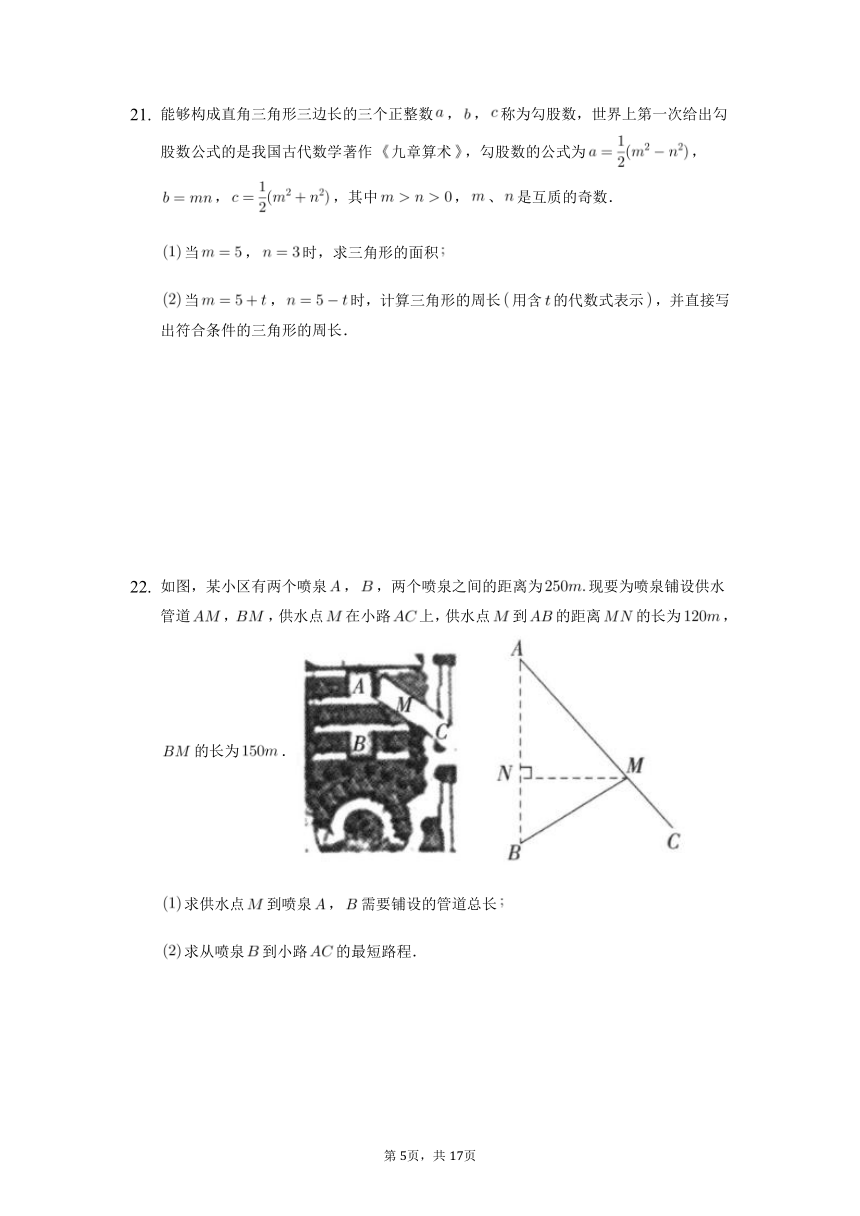
能够构成直角三角形三边长的三个正整数,,称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作九章算术,勾股数的公式为,,,其中,、是互质的奇数.
当,时,求三角形的面积
当,时,计算三角形的周长用含的代数式表示,并直接写出符合条件的三角形的周长.
如图,某小区有两个喷泉,,两个喷泉之间的距离为现要为喷泉铺设供水管道,,供水点在小路上,供水点到的距离的长为,的长为.
求供水点到喷泉,需要铺设的管道总长
求从喷泉到小路的最短路程.
如图,笔直的公路上、两点相距,、为两村庄,于点,于点,已知,,现在要在公路的段上建一个土特产品收购站,使得、两村到收购站的距离相等,则收购站应建在离点多远处?
答案和解析
1.【答案】
【解析】解:由勾股定理可得:斜边,
故选:.
利用勾股定理可以求出斜边即可.
本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
2.【答案】
【解析】解:在中,,,,
,
,
,
解得.
故选C.
首先利用勾股定理计算出的长,再根据三角形的面积公式计算出的长即可.
此题主要考查了勾股定理,以及三角形的面积,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
3.【答案】
【解析】解:在中,,
,,,
.
,,
.
故选:.
根据勾股定理与正方形的性质解答.
本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
4.【答案】
【解析】解:正方形小方格边长为,
,,,
在中,,
,
网格中的是直角三角形.
故选A.
根据勾股定理求得各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解答此题要用到勾股定理的逆定理:已知三角形的三边满足,则三角形是直角三角形.
5.【答案】
【解析】
【分析】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.判定是否为直角三角形,这里给出三边的长,只要验证两小边的平方和是否等于最长边的平方即可.
【解答】
解:正整数,,最大是不是勾股数,关键看三个正整数是否满足:.
,,,是勾股数
,,,是勾股数
,,,不是勾股数
,,,不是勾股数.
故选B.
6.【答案】
【解析】解:、,,
,
为直角三角形,故此选项不合题意;
B、,
能构成直角三角形,故此选项不符合题意;
C、,即,
,
能构成直角三角形,故此选项不符合题意;
D、设,,,
,
解得:,
则,
不是直角三角形,故此选项符合题意.
故选:.
根据三角形内角和定理可分析出、的正误;根据勾股定理逆定理可分析出、的正误.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
7.【答案】
【解析】略
8.【答案】
【解析】
【分析】
本题考查了勾股定理的逆定理,掌握勾股定理的逆定理是解决问题的关键,直接利用勾股定理的逆定理,进而结合直角三角形的面积求法得出答案即可.
【解答】
解:,
三条边长分别为里,里,里,构成了直角三角形,
面积为平方米平方千米.
故选A.
9.【答案】
【解析】
【分析】
本题主要考查的是勾股定理,等腰三角形的性质,三角形的面积的有关知识由题意过作,利用等腰三角形的性质和勾股定理求出,然后再利用三角形的面积公式求解即可.
【解答】
解:如图,作,
是等腰三角形,
,,
.
则的面积为.
故答案为.
10.【答案】
【解析】
【分析】
此题考查了勾股定理及其逆定理,等腰直角三角形的判定与性质,求出、、的长,判断出是等腰直角三角形是解答本题的关键,难度一般.设小正方形的边长为,连接,利用勾股定理求出、、的长,由勾股定理的逆定理判断出是等腰直角三角形,继而得出的度数.
【解答】
解:如图,设小正方形的边长为,连接.
则,,,
,且,
是等腰直角三角形,
.
故答案为.
11.【答案】或
【解析】
【分析】
本题考查的是勾股定理,分类讨论有关知识,类讨论,当为直角边时,当为斜边时,依次求出答案即可.
【解答】
解:当是直角边时,斜边,此时第三边为;
当为斜边时,此时第三边,
综上可得第三边的长度为或
故答案为或.
12.【答案】
【解析】解:设,
,
.
在中,,
,即.
故答案为:.
设,可知,再根据勾股定理列方程即可得出结论.
本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
13.【答案】直角三角形
【解析】
【分析】
本题主要三角形的知识,解答本题的关键是知道勾股定理的逆定理,先求出,,然后再判断三角形的形状.
【解答】
解:,
,,,
,,.
,
是直角三角形,
故答案为直角三角形.
14.【答案】
【解析】
【分析】此题要能够根据勾股定理列出方程,熟练求得方程的解.
设直角三角形的斜边是,则另一条直角边是根据勾股定理列方程求解.
【解答】解:设直角三角形的斜边是,则另一条直角边是.
根据勾股定理,得
,
解,得
.
则斜边的长是.
故答案为
15.【答案】,, ,, ,,
【解析】解:符合即可,例如,,;,,;,,答案不唯一
根据勾股定理的逆定理只要写出的数据符合即可,例如,,;,,;,,.
此题属开放性题目,解答此题要用到勾股定理的逆定理:已知三角形的三边满足,则三角形是直角三角形,只要写出的数据符合即可.
16.【答案】
【解析】
【分析】
本题考查轴对称的性质,等边三角形的性质,勾股定理,含角的直角三角形的性质等知识,解题的关键是判断出何时的长取得最小值,属于中考常考题型.
过点作于,连接首先证明,推出点在射线上运动,根据垂线段最短可知,当点与重合时,的值最小,最小值的长,即可解答.
【解答】
解:过点作于,连接.
是等边三角形,,
,
线段与线段关于直线对称,
,,
点在射线上运动,
根据垂线段最短可知,当点与重合时,的值最小,
在中,,
,
,
的最小值为,
,
此时,,
故答案为.
17.【答案】解:因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
所以.
【解析】见答案.
18.【答案】解:在中,,,,
;
垂直平分,
,
设,则,
,
解得:,
,
.
【解析】 本题考查了线段垂直平分线的性质,勾股定理,熟练掌握线段垂直平分线的性质是解题的关键.
根据勾股定理即可得到结论;
设,则,根据勾股定理列方程,即可得到结论.
19.【答案】解:中,,,,
;
证明:在中,,,,
,
是直角三角形.
【解析】本题考查了勾股定理及其逆定理.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.勾股定理的逆定理:如果三角形的三边长,,满足,那么这个三角形就是直角三角形.掌握定理是解题的关键.
在中,根据勾股定理即可求得的长;
利用勾股定理逆定理即可证明是直角三角形.
20.【答案】解:勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为 、,斜边为 ,.
,, ,
,
即 .
,
.
.
【解析】用文字及符号语言叙述勾股定理即可;
如图,根据四个全等的直角三角形的面积小正方形的面积大正方形的面积,代入数值,即可证明;
利用的结论进行解答.
本题考查了勾股定理的证明.求面积时,利用了“分割法”.
21.【答案】解:当,时,
,,,
,
长度为,的边是直角边,
三角形的面积为.
,
当,时,
,
三角形的周长为,
,、是互质的奇数,
,
.
符合条件的三角形的周长为.
【解析】略
22.【答案】解:在中,
,
,
,
在中,
,
,
供水点到喷泉,需要铺设的管道总长.
,,,
,
是直角三角形,
,
从喷泉到小路的最短路程是.
【解析】见答案.
23.【答案】解:使得,两村到站的距离相等.
,
于,于,
,
,,
,
设,则,
,,
,
解得:,
,
收购站应建在离点处.
【解析】本题主要是运用勾股定理将两个直角三角形的斜边表示出来,两边相等求解即可.
根据使得,两村到站的距离相等,可得,设,则,再分别在和中利用勾股定理,建立关于的方程,求解即可.
第2页,共2页
第1页,共1页
一、选择题(本大题共8小题,共24.0分)
若直角三角形两直角边长分别为和,则斜边的长为
A. B. C. D.
如图,在中,,,,于,则的长是
A. B. C. D.
如图,分别以直角三边为边向外作三个正方形,其面积分别用、、表示,若,,那么
A. B. C. D.
如图,正方形小方格的边长为,则网格中的是
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上答案都不对
下列四组数:,,,,,,,,其中是勾股数的有
A. 组 B. 组 C. 组 D. 组
下列条件中,不能判定是直角三角形的是
A. B. ::::
C. D. ::::
要从电线杆上离地面处向地面拉一根长的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A. B. C. D.
我国南宋著名数学家秦九韶的著作数书九章里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,问这块沙田面积有多大?题中“里”是我国市制长度单位,里米,则该沙田的面积为
A. 平方千米 B. 平方千米 C. 平方千米 D. 平方千米
二、填空题(本大题共8小题,共32.0分)
如果等腰三角形的腰长为,底边长为,那么它的面积为_________.
如图是“俄罗斯方块”游戏中的一个图案,由四个完全相同的小正方形拼成,则的度数为________.
已知直角三角形的两边长分别为和,则第三边长为_____________.
九章算术是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长,如果设,则可列方程为______.
若的三边,,满足,则的形状为________________.
若一个直角三角形的一条直角边长是,另一条直角边比斜边短,斜边的长是______.
将勾股数,,扩大倍,倍,倍,,可以得到勾股数,,;,,;,,;,则我们把,,这样的勾股数称为基本勾股数,请你也写出三组基本勾股数______,______,______.
如图,等边中,,且,是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点运动的过程中,当的长取得最小值时,的长为__________.
三、解答题(本大题共7小题,共64.0分)
如图,在中,,垂足为,,,.
求的长.
求的长.
如图,在中,,,,的垂直平分线分别交、于点、,
求的长度;求的长.
如图,在中,,,,点是外一点,连接,,且,.
求的长;
求证:是直角三角形.
我国古代数学家赵爽曾用图证明了勾股定理,这个图形被称为“弦图”年在北京召开的国际数学家大会的会标图,其图案正是由“弦图”演变而来.“弦图”是由个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.请你根据图解答下列问题:
叙述勾股定理用文字及符号语言叙述;
证明勾股定理;
若大正方形的面积是,小正方形的面积是,求的值.
能够构成直角三角形三边长的三个正整数,,称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作九章算术,勾股数的公式为,,,其中,、是互质的奇数.
当,时,求三角形的面积
当,时,计算三角形的周长用含的代数式表示,并直接写出符合条件的三角形的周长.
如图,某小区有两个喷泉,,两个喷泉之间的距离为现要为喷泉铺设供水管道,,供水点在小路上,供水点到的距离的长为,的长为.
求供水点到喷泉,需要铺设的管道总长
求从喷泉到小路的最短路程.
如图,笔直的公路上、两点相距,、为两村庄,于点,于点,已知,,现在要在公路的段上建一个土特产品收购站,使得、两村到收购站的距离相等,则收购站应建在离点多远处?
答案和解析
1.【答案】
【解析】解:由勾股定理可得:斜边,
故选:.
利用勾股定理可以求出斜边即可.
本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
2.【答案】
【解析】解:在中,,,,
,
,
,
解得.
故选C.
首先利用勾股定理计算出的长,再根据三角形的面积公式计算出的长即可.
此题主要考查了勾股定理,以及三角形的面积,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
3.【答案】
【解析】解:在中,,
,,,
.
,,
.
故选:.
根据勾股定理与正方形的性质解答.
本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
4.【答案】
【解析】解:正方形小方格边长为,
,,,
在中,,
,
网格中的是直角三角形.
故选A.
根据勾股定理求得各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解答此题要用到勾股定理的逆定理:已知三角形的三边满足,则三角形是直角三角形.
5.【答案】
【解析】
【分析】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.判定是否为直角三角形,这里给出三边的长,只要验证两小边的平方和是否等于最长边的平方即可.
【解答】
解:正整数,,最大是不是勾股数,关键看三个正整数是否满足:.
,,,是勾股数
,,,是勾股数
,,,不是勾股数
,,,不是勾股数.
故选B.
6.【答案】
【解析】解:、,,
,
为直角三角形,故此选项不合题意;
B、,
能构成直角三角形,故此选项不符合题意;
C、,即,
,
能构成直角三角形,故此选项不符合题意;
D、设,,,
,
解得:,
则,
不是直角三角形,故此选项符合题意.
故选:.
根据三角形内角和定理可分析出、的正误;根据勾股定理逆定理可分析出、的正误.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
7.【答案】
【解析】略
8.【答案】
【解析】
【分析】
本题考查了勾股定理的逆定理,掌握勾股定理的逆定理是解决问题的关键,直接利用勾股定理的逆定理,进而结合直角三角形的面积求法得出答案即可.
【解答】
解:,
三条边长分别为里,里,里,构成了直角三角形,
面积为平方米平方千米.
故选A.
9.【答案】
【解析】
【分析】
本题主要考查的是勾股定理,等腰三角形的性质,三角形的面积的有关知识由题意过作,利用等腰三角形的性质和勾股定理求出,然后再利用三角形的面积公式求解即可.
【解答】
解:如图,作,
是等腰三角形,
,,
.
则的面积为.
故答案为.
10.【答案】
【解析】
【分析】
此题考查了勾股定理及其逆定理,等腰直角三角形的判定与性质,求出、、的长,判断出是等腰直角三角形是解答本题的关键,难度一般.设小正方形的边长为,连接,利用勾股定理求出、、的长,由勾股定理的逆定理判断出是等腰直角三角形,继而得出的度数.
【解答】
解:如图,设小正方形的边长为,连接.
则,,,
,且,
是等腰直角三角形,
.
故答案为.
11.【答案】或
【解析】
【分析】
本题考查的是勾股定理,分类讨论有关知识,类讨论,当为直角边时,当为斜边时,依次求出答案即可.
【解答】
解:当是直角边时,斜边,此时第三边为;
当为斜边时,此时第三边,
综上可得第三边的长度为或
故答案为或.
12.【答案】
【解析】解:设,
,
.
在中,,
,即.
故答案为:.
设,可知,再根据勾股定理列方程即可得出结论.
本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
13.【答案】直角三角形
【解析】
【分析】
本题主要三角形的知识,解答本题的关键是知道勾股定理的逆定理,先求出,,然后再判断三角形的形状.
【解答】
解:,
,,,
,,.
,
是直角三角形,
故答案为直角三角形.
14.【答案】
【解析】
【分析】此题要能够根据勾股定理列出方程,熟练求得方程的解.
设直角三角形的斜边是,则另一条直角边是根据勾股定理列方程求解.
【解答】解:设直角三角形的斜边是,则另一条直角边是.
根据勾股定理,得
,
解,得
.
则斜边的长是.
故答案为
15.【答案】,, ,, ,,
【解析】解:符合即可,例如,,;,,;,,答案不唯一
根据勾股定理的逆定理只要写出的数据符合即可,例如,,;,,;,,.
此题属开放性题目,解答此题要用到勾股定理的逆定理:已知三角形的三边满足,则三角形是直角三角形,只要写出的数据符合即可.
16.【答案】
【解析】
【分析】
本题考查轴对称的性质,等边三角形的性质,勾股定理,含角的直角三角形的性质等知识,解题的关键是判断出何时的长取得最小值,属于中考常考题型.
过点作于,连接首先证明,推出点在射线上运动,根据垂线段最短可知,当点与重合时,的值最小,最小值的长,即可解答.
【解答】
解:过点作于,连接.
是等边三角形,,
,
线段与线段关于直线对称,
,,
点在射线上运动,
根据垂线段最短可知,当点与重合时,的值最小,
在中,,
,
,
的最小值为,
,
此时,,
故答案为.
17.【答案】解:因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
所以.
【解析】见答案.
18.【答案】解:在中,,,,
;
垂直平分,
,
设,则,
,
解得:,
,
.
【解析】 本题考查了线段垂直平分线的性质,勾股定理,熟练掌握线段垂直平分线的性质是解题的关键.
根据勾股定理即可得到结论;
设,则,根据勾股定理列方程,即可得到结论.
19.【答案】解:中,,,,
;
证明:在中,,,,
,
是直角三角形.
【解析】本题考查了勾股定理及其逆定理.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.勾股定理的逆定理:如果三角形的三边长,,满足,那么这个三角形就是直角三角形.掌握定理是解题的关键.
在中,根据勾股定理即可求得的长;
利用勾股定理逆定理即可证明是直角三角形.
20.【答案】解:勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为 、,斜边为 ,.
,, ,
,
即 .
,
.
.
【解析】用文字及符号语言叙述勾股定理即可;
如图,根据四个全等的直角三角形的面积小正方形的面积大正方形的面积,代入数值,即可证明;
利用的结论进行解答.
本题考查了勾股定理的证明.求面积时,利用了“分割法”.
21.【答案】解:当,时,
,,,
,
长度为,的边是直角边,
三角形的面积为.
,
当,时,
,
三角形的周长为,
,、是互质的奇数,
,
.
符合条件的三角形的周长为.
【解析】略
22.【答案】解:在中,
,
,
,
在中,
,
,
供水点到喷泉,需要铺设的管道总长.
,,,
,
是直角三角形,
,
从喷泉到小路的最短路程是.
【解析】见答案.
23.【答案】解:使得,两村到站的距离相等.
,
于,于,
,
,,
,
设,则,
,,
,
解得:,
,
收购站应建在离点处.
【解析】本题主要是运用勾股定理将两个直角三角形的斜边表示出来,两边相等求解即可.
根据使得,两村到站的距离相等,可得,设,则,再分别在和中利用勾股定理,建立关于的方程,求解即可.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
