2021-2022学年度人教版九年级数学上册课件:25.2.2 运用画树状图法求概率(19张)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学上册课件:25.2.2 运用画树状图法求概率(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 16:02:44 | ||
图片预览





文档简介
(共19张PPT)
RJ九(上)
教学课件
第二十五章 概率初步
25.2 用列举法求概率
25.2.2 运用画树状图法求概率
1.进一步理解等可能事件概率的意义.
2.掌握运用画树状图法计算事件概率的方法.
3.能用画树状图法解决求简单事件概率的问题.
学习目标
问题1 通过上节课的学习,你掌握了用什么方法求概率?
问题2 课堂上,老师提出一个问题,有很多同学举手想来回答.
(1)如果老师就从甲、乙、丙三位同学中随机地选择一位来回答,那么选中丙同学的概率是多少?
直接列举法、列表法.
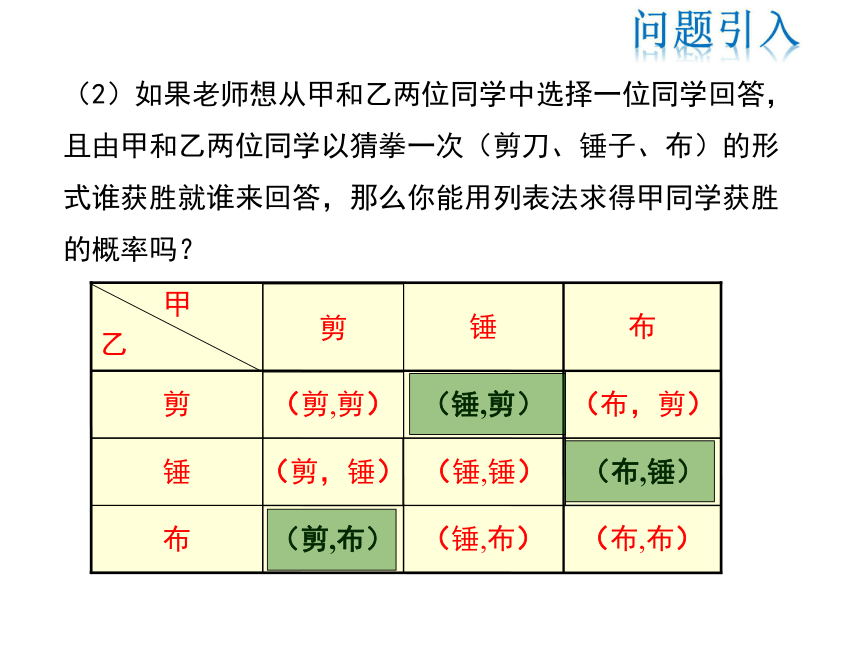
(2)如果老师想从甲和乙两位同学中选择一位同学回答,且由甲和乙两位同学以猜拳一次(剪刀、锤子、布)的形式谁获胜就谁来回答,那么你能用列表法求得甲同学获胜的概率吗?
布
锤
(布,锤)
(布,布)
(锤,布)
(剪,布)
(锤,锤)
(剪,锤)
(布,剪)
(锤,剪)
(剪,剪)
剪
布
锤
剪
乙
甲
由表可以看出,甲和乙两位同学猜拳可能出现的结果有9个,它们出现的可能性相等.其中能确定胜负的结果有6个,而满足甲同学赢(记为事件B)的结果有3个,即:锤剪、布锤 、剪布、所以
问题3 上述问题如果老师想让甲、乙、丙三位同学猜拳(剪刀、锤子、布) ,由最先一次猜拳就获胜的同学来回答,那么你能用列表法算出甲同学获胜的概率吗?
若再用列表法表示所有结果已经不方便!
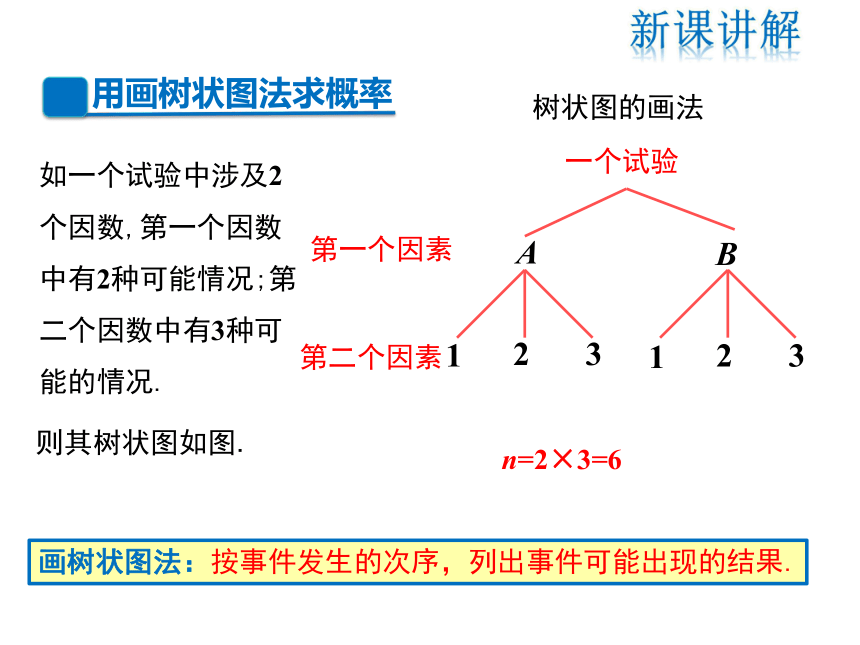
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树状图如图.
n=2×3=6
画树状图法:按事件发生的次序,列出事件可能出现的结果.
用画树状图法求概率
甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
I
H
D
E
C
A
B
(1)取出的3个小球中上恰好有1个,2个和3个写有元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
例题
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果有12种,它们出现的可能性相等.
用树状图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树状图法求事件的概率很有效.
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
满足三个全部为元音字母的结果有1个,则 P(三个元音)=
(1)满足只有一个元音字母的结果有5个,则 P(一个元音)=
(2)满足全是辅音字母的结果有2个,则 P(三个辅音)= = .
★画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
★列举法求概率的选择
1.口袋中有3个白球,1个红球,从中任意摸出2个球,2个球颜色不同的概率为( )
2.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
B
8
A. B. C. D.
3.在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同.先从盒子里随机取出一个小球,记下数字后放回盒子里,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法求下列事件的概率:
(1)两次取出的小球上的数字相同;
(2)两次取出的小球上的数字之和大于10.
(1)两次取出的小球上的数字相同的可能性只有3种,所以P(数字相同)=
(2)两次取出的小球上的数字之和大于10的可能性只有4种,所以P(数字之和大于10)=
解:根据题意,画出树状图如下
第一个数字
第二个数字
6
6
-2
7
-2
6
-2
7
7
6
-2
7
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
第一辆
左
右
左
右
左直右
第二辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
第三辆
可能出现的结果共有27种,且这些结果出现的可能性相等.
(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)=
解:根据题意画出树状图如下:
(1)P(三辆车全部直行)=
画树状图法
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
RJ九(上)
教学课件
第二十五章 概率初步
25.2 用列举法求概率
25.2.2 运用画树状图法求概率
1.进一步理解等可能事件概率的意义.
2.掌握运用画树状图法计算事件概率的方法.
3.能用画树状图法解决求简单事件概率的问题.
学习目标
问题1 通过上节课的学习,你掌握了用什么方法求概率?
问题2 课堂上,老师提出一个问题,有很多同学举手想来回答.
(1)如果老师就从甲、乙、丙三位同学中随机地选择一位来回答,那么选中丙同学的概率是多少?
直接列举法、列表法.
(2)如果老师想从甲和乙两位同学中选择一位同学回答,且由甲和乙两位同学以猜拳一次(剪刀、锤子、布)的形式谁获胜就谁来回答,那么你能用列表法求得甲同学获胜的概率吗?
布
锤
(布,锤)
(布,布)
(锤,布)
(剪,布)
(锤,锤)
(剪,锤)
(布,剪)
(锤,剪)
(剪,剪)
剪
布
锤
剪
乙
甲
由表可以看出,甲和乙两位同学猜拳可能出现的结果有9个,它们出现的可能性相等.其中能确定胜负的结果有6个,而满足甲同学赢(记为事件B)的结果有3个,即:锤剪、布锤 、剪布、所以
问题3 上述问题如果老师想让甲、乙、丙三位同学猜拳(剪刀、锤子、布) ,由最先一次猜拳就获胜的同学来回答,那么你能用列表法算出甲同学获胜的概率吗?
若再用列表法表示所有结果已经不方便!
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树状图如图.
n=2×3=6
画树状图法:按事件发生的次序,列出事件可能出现的结果.
用画树状图法求概率
甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
I
H
D
E
C
A
B
(1)取出的3个小球中上恰好有1个,2个和3个写有元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
例题
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果有12种,它们出现的可能性相等.
用树状图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树状图法求事件的概率很有效.
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
满足三个全部为元音字母的结果有1个,则 P(三个元音)=
(1)满足只有一个元音字母的结果有5个,则 P(一个元音)=
(2)满足全是辅音字母的结果有2个,则 P(三个辅音)= = .
★画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
★列举法求概率的选择
1.口袋中有3个白球,1个红球,从中任意摸出2个球,2个球颜色不同的概率为( )
2.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
B
8
A. B. C. D.
3.在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同.先从盒子里随机取出一个小球,记下数字后放回盒子里,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法求下列事件的概率:
(1)两次取出的小球上的数字相同;
(2)两次取出的小球上的数字之和大于10.
(1)两次取出的小球上的数字相同的可能性只有3种,所以P(数字相同)=
(2)两次取出的小球上的数字之和大于10的可能性只有4种,所以P(数字之和大于10)=
解:根据题意,画出树状图如下
第一个数字
第二个数字
6
6
-2
7
-2
6
-2
7
7
6
-2
7
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
第一辆
左
右
左
右
左直右
第二辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
第三辆
可能出现的结果共有27种,且这些结果出现的可能性相等.
(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)=
解:根据题意画出树状图如下:
(1)P(三辆车全部直行)=
画树状图法
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
同课章节目录
