2021-2022学年度人教版七年级数学上册课件 第一章 复习课(共30张PPT)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学上册课件 第一章 复习课(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 17:00:32 | ||
图片预览










文档简介
(共30张PPT)
RJ七(上)
教学课件
第一章 有理数
复习课
二、有理数
1.有理数的概念
2.用正、负数表示具有相反意义的量
1.小学学过的除0以外的数都是正数.
在正数前面加上符号“-”(负)的数叫做负数.
一、正数和负数
整数和分数统称有理数
3.数轴
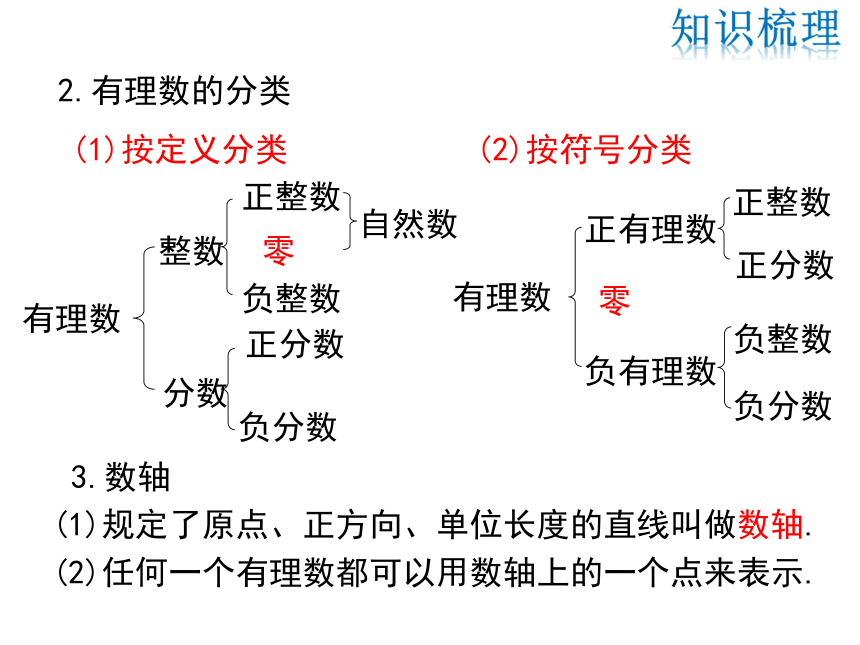
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数
正整数
正分数
整数
分数
零
负整数
自然数
2.有理数的分类
负分数
(1)按定义分类
(2)按符号分类
(1)规定了原点、正方向、单位长度的直线叫做数轴.
(2)任何一个有理数都可以用数轴上的一个点来表示.
4.相反数
(1)只有符号不同的两个数叫做互为相反数
(2)互为相反数的两个数到原点的距离相等
5.绝对值
(1)一个数在数轴上对应的点到原点的距离
叫做这个数的绝对值
(2)一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
三、有理数的运算
6.有理数大小的比较
(1)数轴上表示的两个数,右边的总比左边的大.
(2)正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
1.有理数的加法
(1)加法法则
(2)加法的运算律
加法的交换律
加法的结合律
2.有理数的减法
减法法则:
减去一个数,等于加上这个数的相反数.
3.有理数的乘法
(1)乘法法则
(2)乘法的运算律
乘法的交换律
乘法的结合律
4.有理数的除法
乘法的分配律
除法法则:
除以一个数,等于乘以这个数的倒数.
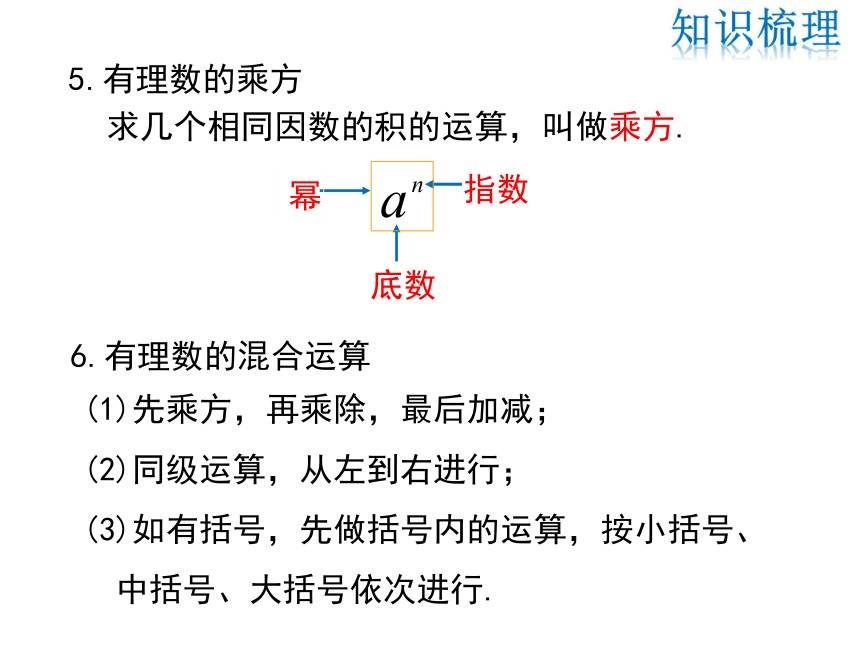
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
5.有理数的乘方
求几个相同因数的积的运算,叫做乘方.
指数
底数
6.有理数的混合运算
幂
四、科学记数法
五、近似数
1.按照要求取近似数
2.由近似数判断精确度
四舍五入到某一位,就说这个数近似数精确到那一位.
1.1≤a<10
2.n为原数的整数位减去1
把大于10的数记成a×10n的形式,其中
正、负数的意义
例1 如果-4米表示向东走4米,那么向西走2米记作_____.
+2米
【解析】根据题意,可知向东记为负,向西记为正,
故向西走2米记做+2米.
方法总结:根据相反意义合理使用正、负数对实际问题进行表示.一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负
注意带单位
考点1
1.下列语句中,含有相反意义的两个量是( )
A.盈利1千元和收入2千元 B.上升8米和后退8米
C.存入1千元和取出2千元 D.超过2厘米和上涨2厘米
C
-8
2.上升9记作+9,那么下降8记作____.
正、负数的概念
例2 判断:
①不带“-”号的数都是正数 ( )
④一个有理数不是正数就是负数 ( )
⑤ 0℃表示没有温度 ( )
②如果a是正数,那么-a一定是负( )
③不存在既不是正数,也不是负数的数( )
×
×
×
×
√
【解析】①0不带“-”号,但0不是正数,故①错误;②正数的相反数是负数,故②正确;③同①,故③错误;④同③,故④错误;⑤0℃并不是表示没有温度,它是介于正温度与负温度之间,故⑤错误.
考点2
方法总结:0既不是正数也不是负数,0的相反数是它本身.0不仅能表示没有,而且表示正、负之间的分界值.
有理数的分类
例3 将下列各数分别填入下列相应的圈内:
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
, , , , , , ,
正数
负数
整数
分数
3.5,
|-2|,
0.5
-3.5
,-2
,-1
3
5
,-
1
3
0
,|-2|
,-2
3.5,
,0.5
-3.5,
-1
3
5
,-
1
3
考点3
+3.5
0
-2
-
2
3
-0.7
3.在 ,, , , , 中,负分数有 个.
11
2
【解析】负分数不仅是负数而且是分数,注意小数也属于分数.故只有2个.
相反数、倒数、绝对值
例4 填表
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
数
相反数
倒数
绝对值
-3.5
-2
0
3.5
2
-0.5
1
3
5
1
3
3.5
2
0
3.5
2
0.5
1
3
5
1
3
-3
没有
-0.5
2
0.5
-
2
7
2
7
-
5
8
考点4
4. 的倒数是 ; 的相反数是 ;
-
1
3
-1
1
3
1
1
3
-3
–5的绝对值是 .
5
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
数轴
例5 请你将下面的数在数轴上表示出来
-1
3
5
-
1
3
解:表示如下
-4
-2
-1
0
1
2
3
4
-3
3.5
-3.5
0
|-2|
-2
0.5
-1
3
5
-
1
3
考点5
5.在数轴上,点A所表示的数为2,那么到点A的距离
等于3个单位长度的点所表示的数是________.
-1或3
有理数比较大小
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
例6 请你将下面的数用“>”连接起来
-1
3
5
-
1
3
解法一:将各数在数轴上表示出来,右边的大于左边的,然后从大到小排列
-4
-2
-1
0
1
2
3
4
-3
3.5
-3.5
0
|-2|
-2
0.5
-1
3
5
-
1
3
> > > > > > >
3.5
|-2|
0
-3.5
-2
0.5
-1
3
5
-
1
3
考点6
解法二:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
> > > > > > >
3.5
|-2|
0
-3.5
-2
0.5
-1
3
5
-
1
3
6.某日零点,北京、上海、宁夏的气温分别是﹣4℃、5℃、6℃、﹣8℃,当时这四个城市中,气温最低的是 ( )
A.北京 B.上海 C.重庆 D.宁夏
D
科学记数法
例7 将数13 445 000 000 000km用科学记数法
表示_ _______m.
1.3445×1016
注意统一单位
7.2016年末上海市常住人口总数为2419.7万人,用科学记数法表示为 人.
2.4197×107
考点7
近似数
例8 2016年我国全年出境旅游人数达1.22亿人次.这里的1.22亿精确到 位.
百万
8.由四舍五入法得到的近似数2.349×105精确到
位,如果精确到万位可写成 .
2.3×105
百
考点8
有理数的运算
例9 计算
(1)
(2)
(3)
(4)
考点9
1.把减法转化为加法时,要注意符号.
2.对几个有理数相加减的题目,要注意观察,将哪些数放在一起会使计算简便
解:(1)
(2)
注意符号问题
(3)
先确定商的符号,再把绝对值相除
注意:1.底数是带分数时,要先将带分数化成假分数.2.区分-24与(-2)4.
(4)
9.计算
(1)
(2)
(3)
(4)
答案:(1)-17
(2)33
(3)-3.3
整数
分数
数轴
比较大小
相反数
绝对值
点与数的对应
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
减法
运算
加法
乘法
乘方
除法
交换律
结合律
RJ七(上)
教学课件
第一章 有理数
复习课
二、有理数
1.有理数的概念
2.用正、负数表示具有相反意义的量
1.小学学过的除0以外的数都是正数.
在正数前面加上符号“-”(负)的数叫做负数.
一、正数和负数
整数和分数统称有理数
3.数轴
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数
正整数
正分数
整数
分数
零
负整数
自然数
2.有理数的分类
负分数
(1)按定义分类
(2)按符号分类
(1)规定了原点、正方向、单位长度的直线叫做数轴.
(2)任何一个有理数都可以用数轴上的一个点来表示.
4.相反数
(1)只有符号不同的两个数叫做互为相反数
(2)互为相反数的两个数到原点的距离相等
5.绝对值
(1)一个数在数轴上对应的点到原点的距离
叫做这个数的绝对值
(2)一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
三、有理数的运算
6.有理数大小的比较
(1)数轴上表示的两个数,右边的总比左边的大.
(2)正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
1.有理数的加法
(1)加法法则
(2)加法的运算律
加法的交换律
加法的结合律
2.有理数的减法
减法法则:
减去一个数,等于加上这个数的相反数.
3.有理数的乘法
(1)乘法法则
(2)乘法的运算律
乘法的交换律
乘法的结合律
4.有理数的除法
乘法的分配律
除法法则:
除以一个数,等于乘以这个数的倒数.
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
5.有理数的乘方
求几个相同因数的积的运算,叫做乘方.
指数
底数
6.有理数的混合运算
幂
四、科学记数法
五、近似数
1.按照要求取近似数
2.由近似数判断精确度
四舍五入到某一位,就说这个数近似数精确到那一位.
1.1≤a<10
2.n为原数的整数位减去1
把大于10的数记成a×10n的形式,其中
正、负数的意义
例1 如果-4米表示向东走4米,那么向西走2米记作_____.
+2米
【解析】根据题意,可知向东记为负,向西记为正,
故向西走2米记做+2米.
方法总结:根据相反意义合理使用正、负数对实际问题进行表示.一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负
注意带单位
考点1
1.下列语句中,含有相反意义的两个量是( )
A.盈利1千元和收入2千元 B.上升8米和后退8米
C.存入1千元和取出2千元 D.超过2厘米和上涨2厘米
C
-8
2.上升9记作+9,那么下降8记作____.
正、负数的概念
例2 判断:
①不带“-”号的数都是正数 ( )
④一个有理数不是正数就是负数 ( )
⑤ 0℃表示没有温度 ( )
②如果a是正数,那么-a一定是负( )
③不存在既不是正数,也不是负数的数( )
×
×
×
×
√
【解析】①0不带“-”号,但0不是正数,故①错误;②正数的相反数是负数,故②正确;③同①,故③错误;④同③,故④错误;⑤0℃并不是表示没有温度,它是介于正温度与负温度之间,故⑤错误.
考点2
方法总结:0既不是正数也不是负数,0的相反数是它本身.0不仅能表示没有,而且表示正、负之间的分界值.
有理数的分类
例3 将下列各数分别填入下列相应的圈内:
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
, , , , , , ,
正数
负数
整数
分数
3.5,
|-2|,
0.5
-3.5
,-2
,-1
3
5
,-
1
3
0
,|-2|
,-2
3.5,
,0.5
-3.5,
-1
3
5
,-
1
3
考点3
+3.5
0
-2
-
2
3
-0.7
3.在 ,, , , , 中,负分数有 个.
11
2
【解析】负分数不仅是负数而且是分数,注意小数也属于分数.故只有2个.
相反数、倒数、绝对值
例4 填表
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
数
相反数
倒数
绝对值
-3.5
-2
0
3.5
2
-0.5
1
3
5
1
3
3.5
2
0
3.5
2
0.5
1
3
5
1
3
-3
没有
-0.5
2
0.5
-
2
7
2
7
-
5
8
考点4
4. 的倒数是 ; 的相反数是 ;
-
1
3
-1
1
3
1
1
3
-3
–5的绝对值是 .
5
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
数轴
例5 请你将下面的数在数轴上表示出来
-1
3
5
-
1
3
解:表示如下
-4
-2
-1
0
1
2
3
4
-3
3.5
-3.5
0
|-2|
-2
0.5
-1
3
5
-
1
3
考点5
5.在数轴上,点A所表示的数为2,那么到点A的距离
等于3个单位长度的点所表示的数是________.
-1或3
有理数比较大小
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
例6 请你将下面的数用“>”连接起来
-1
3
5
-
1
3
解法一:将各数在数轴上表示出来,右边的大于左边的,然后从大到小排列
-4
-2
-1
0
1
2
3
4
-3
3.5
-3.5
0
|-2|
-2
0.5
-1
3
5
-
1
3
> > > > > > >
3.5
|-2|
0
-3.5
-2
0.5
-1
3
5
-
1
3
考点6
解法二:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
> > > > > > >
3.5
|-2|
0
-3.5
-2
0.5
-1
3
5
-
1
3
6.某日零点,北京、上海、宁夏的气温分别是﹣4℃、5℃、6℃、﹣8℃,当时这四个城市中,气温最低的是 ( )
A.北京 B.上海 C.重庆 D.宁夏
D
科学记数法
例7 将数13 445 000 000 000km用科学记数法
表示_ _______m.
1.3445×1016
注意统一单位
7.2016年末上海市常住人口总数为2419.7万人,用科学记数法表示为 人.
2.4197×107
考点7
近似数
例8 2016年我国全年出境旅游人数达1.22亿人次.这里的1.22亿精确到 位.
百万
8.由四舍五入法得到的近似数2.349×105精确到
位,如果精确到万位可写成 .
2.3×105
百
考点8
有理数的运算
例9 计算
(1)
(2)
(3)
(4)
考点9
1.把减法转化为加法时,要注意符号.
2.对几个有理数相加减的题目,要注意观察,将哪些数放在一起会使计算简便
解:(1)
(2)
注意符号问题
(3)
先确定商的符号,再把绝对值相除
注意:1.底数是带分数时,要先将带分数化成假分数.2.区分-24与(-2)4.
(4)
9.计算
(1)
(2)
(3)
(4)
答案:(1)-17
(2)33
(3)-3.3
整数
分数
数轴
比较大小
相反数
绝对值
点与数的对应
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
减法
运算
加法
乘法
乘方
除法
交换律
结合律
