专题11.7 三角形角平分线几何模型 同步导学(含解析)
文档属性
| 名称 | 专题11.7 三角形角平分线几何模型 同步导学(含解析) | 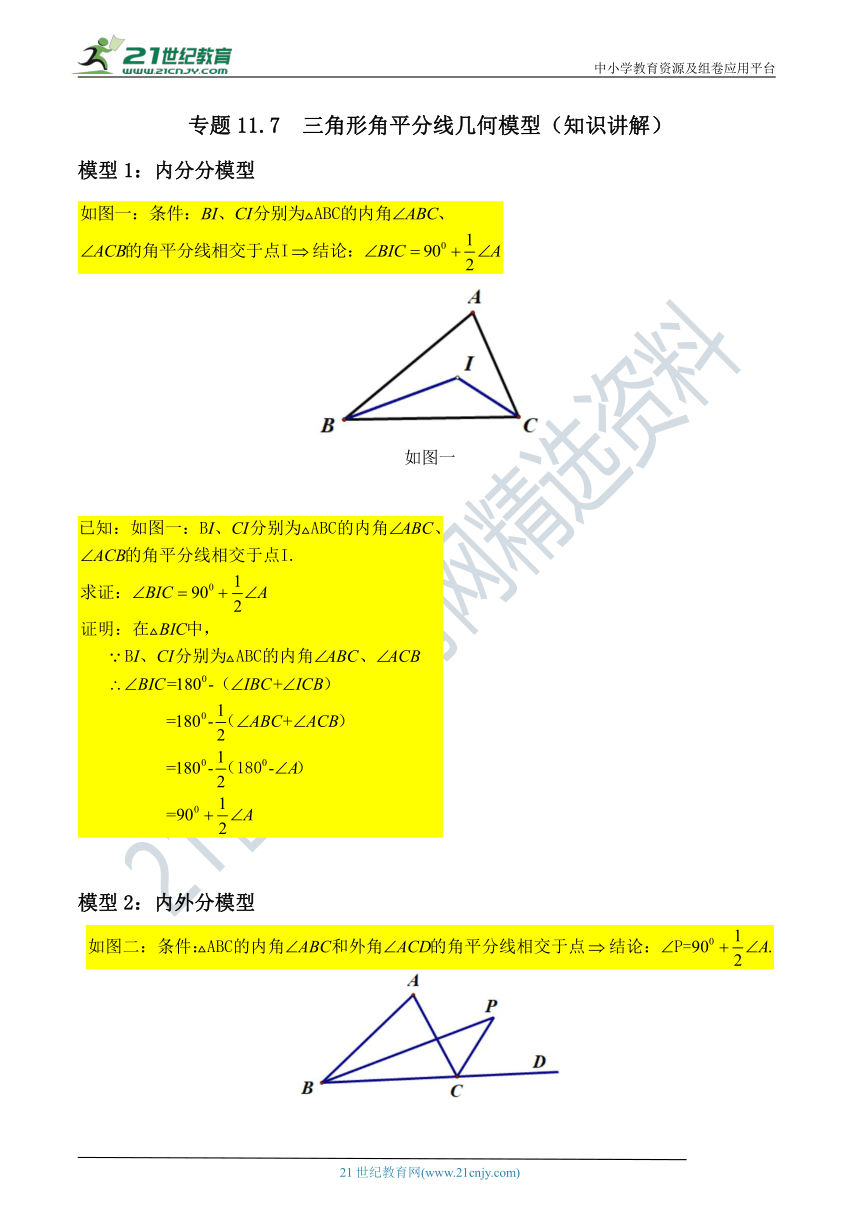 | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 19:49:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题11.7 三角形角平分线几何模型(知识讲解)
模型1:内分分模型
如图一
模型2:内外分模型
如图二
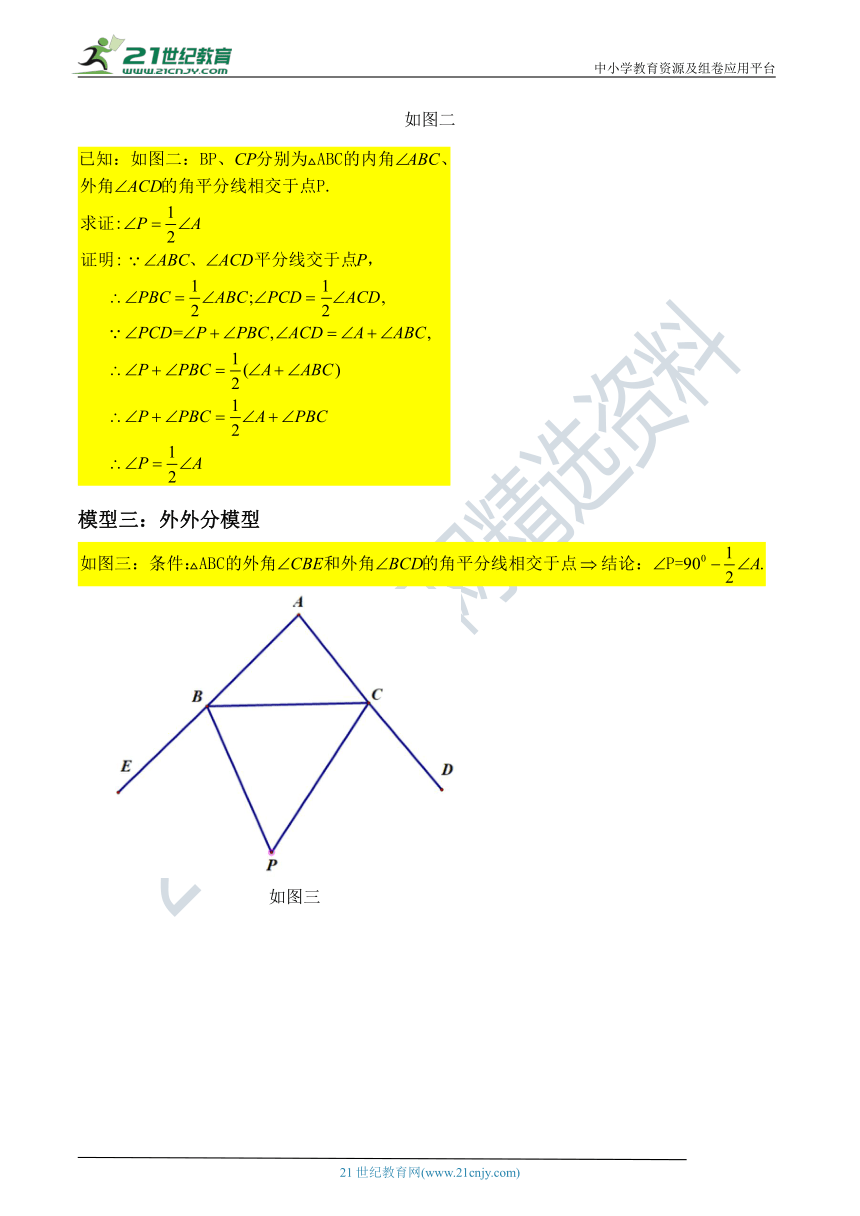
模型三:外外分模型
如图三
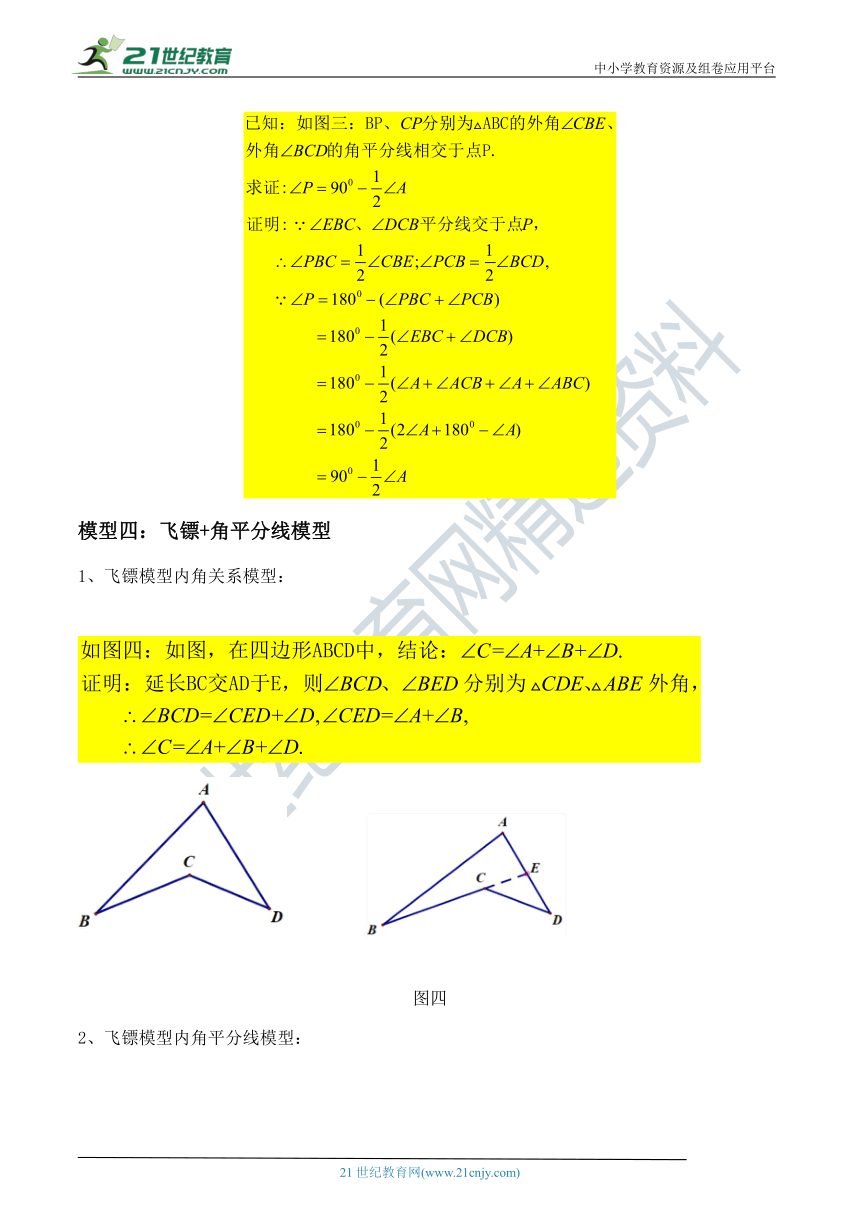
模型四:飞镖+角平分线模型
飞镖模型内角关系模型:
图四
飞镖模型内角平分线模型:
图五
【典型例题】
类型一、内分分模型
1. 如图,的角平分线相交于点.
(1)若,则________;
(2)试探究与之间的数量关系并说明理由.
【答案】(1)60;(2),见解析.
【分析】
(1)直接利用三角形的内角和定理求解即可;
(2)先根据角平分线的定义得到∠1=∠ABC,∠2=∠ACB,再根据三角形内角和定理得∠BPC=180°-∠1-∠2=180°-(∠ABC+∠ACB),加上∠ABC+∠ACB=180°-∠A,易得∠BPC=90°+∠A,再根据平角的定义解答即可.21世纪教育网版权所有
解:(1)∵∠ABC=50°,∠ACB=70°,
∴∠A=180°-50°-70°=60°.
故答案为60.21教育网
(2)∠DPC=90°-∠A ,
理由:的平分线相交于点,,
,
∴∠DPC=180°-(90°+∠A)=90°-∠A.
故答案为:90°-∠A.
【点拨】本题考查了三角形内角和定理:三角形内角和是180°,本题探讨了三角形两角的平分线的夹角与第三个角之间的关系.www.21-cn-jy.com
类型二、内外分模型
2.(2019·全国九年级专题练习)如图,在中,与的平分线相交于,与的平分线相交于,以此类推,与的平分线相交于,求与数量关系.2·1·c·n·j·y
【答案】
【分析】先根据三角形三角形外角的性质及角平分线得出∠A1与∠A的关系,同理得出∠A2与∠A1的关系,从而推导出∠A2与∠A的关系,……,进而归纳出∠An与∠A的关系,即可得出答案.
解:在中,有∠ACD=∠A+∠ABC,
在中,有∠A1CD=∠A1+∠A1BC,
∵与的平分线相交于,
∴∠A1CD=∠ACD,∠A1BC=∠ABC,
∴∠A1=∠A,
同理,∠A2=∠A1,即∠A2=∠A,
由此可得,∠A3=∠A,
……
∴.
【点拨】本题考查了三角形外角的性质、角平分线的性质等知识.根据三角形外角等于不相邻的两个内角的和找出∠A1、∠A2……∠An与A的关系是解题的关键.【来源:21·世纪·教育·网】
类型三、 外分分模型
3.(2020·江苏苏州市·七年级期末)如图1,△ABC的外角平分线交于点F.
(1)若∠A=40°,则∠F的度数为 ;
(2)如图2,过点F作直线MN∥BC,交AB,AC延长线于点M,N,若设∠MFB=α,∠NFC=β,则∠A与α+β的数量关系是 ;21·世纪*教育网
(3)在(2)的条件下,将直线MN绕点F转动.
①如图3,当直线MN与线段BC没有交点时,试探索∠A与α,β之间的数量关系,并说明理由;
②当直线MN与线段BC有交点时,试问①中∠A与α,β之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请给出三者之间的数量关系.www-2-1-cnjy-com
【答案】(1)70°(2) (3)①见解析 ②不成立;或
【分析】
(1)根据三角形内角和定理以及角平分线的定义,即可得到∠F的度数;
(2)根据三角形内角和定理以及角平分线的定义,即可得到∠BFC的度数,再根据平行线的性质,即可得到∠A与α+β的数量关系;21cnjy.com
(3)①根据(2)中的结论∠BFC=90°﹣∠A,以及平角的定义,即可得到∠A与α,β之间的数量关系;
②分两种情况进行讨论,根据(2)中的结论∠BFC=90°﹣∠A,以及平角的定义,即可得到∠A与α,β之间的数量关系.2-1-c-n-j-y
解:(1)如图1,∵∠A=40°,
∴∠ABC+∠ACB=140°,
∴∠DBC+∠ECB=360°﹣140°=220°,
又∵△ABC的外角平分线交于点F,
∴∠FBC+∠FCB=(∠DBC+∠ECB)=×220°=110°,
∴△BCF中,∠F=180°﹣110°=70°,
故答案为:70°;
(2)如图2,∵∠ABC+∠ACB=180°﹣∠A,
∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,
又∵△ABC的外角平分线交于点F,
∴∠FBC+∠FCB=(∠DBC+∠ECB)=×(180°+∠A)=90°+∠A ,
∴△BCF中,∠BFC=180°﹣(90°+∠A )=90°﹣∠A,
又∵∠MFB=α,∠NFC=β,MN∥BC,
∴∠FBC=α,∠FCB=β,
∵△BCF中,∠FBC+∠FCB+∠BFC=180°,
∴α+β+90°﹣∠A=180°,
即α+β﹣∠A=90°,
故答案为:α+β﹣∠A=90°;
(3)①α+β﹣∠A=90°,理由如下:
如图3,由(2)可得,∠BFC=90°﹣∠A,
∵∠MFB+∠NFC+∠BFC=180°,
∴α+β+90°﹣∠A=180°,
即α+β﹣∠A=90°,
②当直线MN与线段BC有交点时,①中∠A与α,β之间的数量关系不成立.
分两种情况:
如图4,当M在线段AB上,N在AC延长线上时,
由(2)可得,∠BFC=90°﹣∠A,
∵∠BFC﹣∠MFB+∠NFC=180°,
∴90°﹣∠A﹣α+β=180°,
即β﹣α﹣∠A=90°;
如图5,当M在AB的延长线上,N在线段AC上时,
由(2)可得,∠BFC=90°﹣∠A,
∵∠BFC﹣∠NFC+∠MFB=180°,
∴90°﹣∠A﹣β+α=180°,
即α﹣β﹣∠A=90°;
综上所述,∠A与α,β之间的数量关系为β﹣α﹣∠A=90°或α﹣β﹣∠A=90°.
【点拨】此题主要考查三角形的角度求解与证明,解题的关键是根据题意分情况作图.
类型四、 飞镖模型
4.(2019·全国九年级单元测试)如图,已知在中,,、分别平分、,相交于点,、分别平分、,相交于点,求、的度数.
【答案】;.
【分析】根据三角形内角平分线的交角的基本图形和结论即可得出答案
解:由三角形内角平分线的交角的基本图形和结论得,;
;
、分别平分、,相交于点,
是的平分线,
.
【点拨】本题考查了三角形的内角和定理,以及三角形的角平分线的性质,熟练掌握相关的知识点是解题的关键.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题11.7 三角形角平分线几何模型(知识讲解)
模型1:内分分模型
如图一
模型2:内外分模型
如图二
模型三:外外分模型
如图三
模型四:飞镖+角平分线模型
飞镖模型内角关系模型:
图四
飞镖模型内角平分线模型:
图五
【典型例题】
类型一、内分分模型
1. 如图,的角平分线相交于点.
(1)若,则________;
(2)试探究与之间的数量关系并说明理由.
【答案】(1)60;(2),见解析.
【分析】
(1)直接利用三角形的内角和定理求解即可;
(2)先根据角平分线的定义得到∠1=∠ABC,∠2=∠ACB,再根据三角形内角和定理得∠BPC=180°-∠1-∠2=180°-(∠ABC+∠ACB),加上∠ABC+∠ACB=180°-∠A,易得∠BPC=90°+∠A,再根据平角的定义解答即可.21世纪教育网版权所有
解:(1)∵∠ABC=50°,∠ACB=70°,
∴∠A=180°-50°-70°=60°.
故答案为60.21教育网
(2)∠DPC=90°-∠A ,
理由:的平分线相交于点,,
,
∴∠DPC=180°-(90°+∠A)=90°-∠A.
故答案为:90°-∠A.
【点拨】本题考查了三角形内角和定理:三角形内角和是180°,本题探讨了三角形两角的平分线的夹角与第三个角之间的关系.www.21-cn-jy.com
类型二、内外分模型
2.(2019·全国九年级专题练习)如图,在中,与的平分线相交于,与的平分线相交于,以此类推,与的平分线相交于,求与数量关系.2·1·c·n·j·y
【答案】
【分析】先根据三角形三角形外角的性质及角平分线得出∠A1与∠A的关系,同理得出∠A2与∠A1的关系,从而推导出∠A2与∠A的关系,……,进而归纳出∠An与∠A的关系,即可得出答案.
解:在中,有∠ACD=∠A+∠ABC,
在中,有∠A1CD=∠A1+∠A1BC,
∵与的平分线相交于,
∴∠A1CD=∠ACD,∠A1BC=∠ABC,
∴∠A1=∠A,
同理,∠A2=∠A1,即∠A2=∠A,
由此可得,∠A3=∠A,
……
∴.
【点拨】本题考查了三角形外角的性质、角平分线的性质等知识.根据三角形外角等于不相邻的两个内角的和找出∠A1、∠A2……∠An与A的关系是解题的关键.【来源:21·世纪·教育·网】
类型三、 外分分模型
3.(2020·江苏苏州市·七年级期末)如图1,△ABC的外角平分线交于点F.
(1)若∠A=40°,则∠F的度数为 ;
(2)如图2,过点F作直线MN∥BC,交AB,AC延长线于点M,N,若设∠MFB=α,∠NFC=β,则∠A与α+β的数量关系是 ;21·世纪*教育网
(3)在(2)的条件下,将直线MN绕点F转动.
①如图3,当直线MN与线段BC没有交点时,试探索∠A与α,β之间的数量关系,并说明理由;
②当直线MN与线段BC有交点时,试问①中∠A与α,β之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请给出三者之间的数量关系.www-2-1-cnjy-com
【答案】(1)70°(2) (3)①见解析 ②不成立;或
【分析】
(1)根据三角形内角和定理以及角平分线的定义,即可得到∠F的度数;
(2)根据三角形内角和定理以及角平分线的定义,即可得到∠BFC的度数,再根据平行线的性质,即可得到∠A与α+β的数量关系;21cnjy.com
(3)①根据(2)中的结论∠BFC=90°﹣∠A,以及平角的定义,即可得到∠A与α,β之间的数量关系;
②分两种情况进行讨论,根据(2)中的结论∠BFC=90°﹣∠A,以及平角的定义,即可得到∠A与α,β之间的数量关系.2-1-c-n-j-y
解:(1)如图1,∵∠A=40°,
∴∠ABC+∠ACB=140°,
∴∠DBC+∠ECB=360°﹣140°=220°,
又∵△ABC的外角平分线交于点F,
∴∠FBC+∠FCB=(∠DBC+∠ECB)=×220°=110°,
∴△BCF中,∠F=180°﹣110°=70°,
故答案为:70°;
(2)如图2,∵∠ABC+∠ACB=180°﹣∠A,
∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,
又∵△ABC的外角平分线交于点F,
∴∠FBC+∠FCB=(∠DBC+∠ECB)=×(180°+∠A)=90°+∠A ,
∴△BCF中,∠BFC=180°﹣(90°+∠A )=90°﹣∠A,
又∵∠MFB=α,∠NFC=β,MN∥BC,
∴∠FBC=α,∠FCB=β,
∵△BCF中,∠FBC+∠FCB+∠BFC=180°,
∴α+β+90°﹣∠A=180°,
即α+β﹣∠A=90°,
故答案为:α+β﹣∠A=90°;
(3)①α+β﹣∠A=90°,理由如下:
如图3,由(2)可得,∠BFC=90°﹣∠A,
∵∠MFB+∠NFC+∠BFC=180°,
∴α+β+90°﹣∠A=180°,
即α+β﹣∠A=90°,
②当直线MN与线段BC有交点时,①中∠A与α,β之间的数量关系不成立.
分两种情况:
如图4,当M在线段AB上,N在AC延长线上时,
由(2)可得,∠BFC=90°﹣∠A,
∵∠BFC﹣∠MFB+∠NFC=180°,
∴90°﹣∠A﹣α+β=180°,
即β﹣α﹣∠A=90°;
如图5,当M在AB的延长线上,N在线段AC上时,
由(2)可得,∠BFC=90°﹣∠A,
∵∠BFC﹣∠NFC+∠MFB=180°,
∴90°﹣∠A﹣β+α=180°,
即α﹣β﹣∠A=90°;
综上所述,∠A与α,β之间的数量关系为β﹣α﹣∠A=90°或α﹣β﹣∠A=90°.
【点拨】此题主要考查三角形的角度求解与证明,解题的关键是根据题意分情况作图.
类型四、 飞镖模型
4.(2019·全国九年级单元测试)如图,已知在中,,、分别平分、,相交于点,、分别平分、,相交于点,求、的度数.
【答案】;.
【分析】根据三角形内角平分线的交角的基本图形和结论即可得出答案
解:由三角形内角平分线的交角的基本图形和结论得,;
;
、分别平分、,相交于点,
是的平分线,
.
【点拨】本题考查了三角形的内角和定理,以及三角形的角平分线的性质,熟练掌握相关的知识点是解题的关键.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
