专题11.9 三角形有关的角-燕尾图形 同步训练(含解析)
文档属性
| 名称 | 专题11.9 三角形有关的角-燕尾图形 同步训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 19:42:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题11.9 三角形有关的角-燕尾模型(专项练习)
如图:这样的图形称之为“燕尾模型”
结论:∠BDC=∠A+∠B+∠C
一、单选题
1.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )21·cn·jy·com
A.50° B.118° C.100° D.90°
2.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.24° B.25° C.30° D.36°
二、填空题
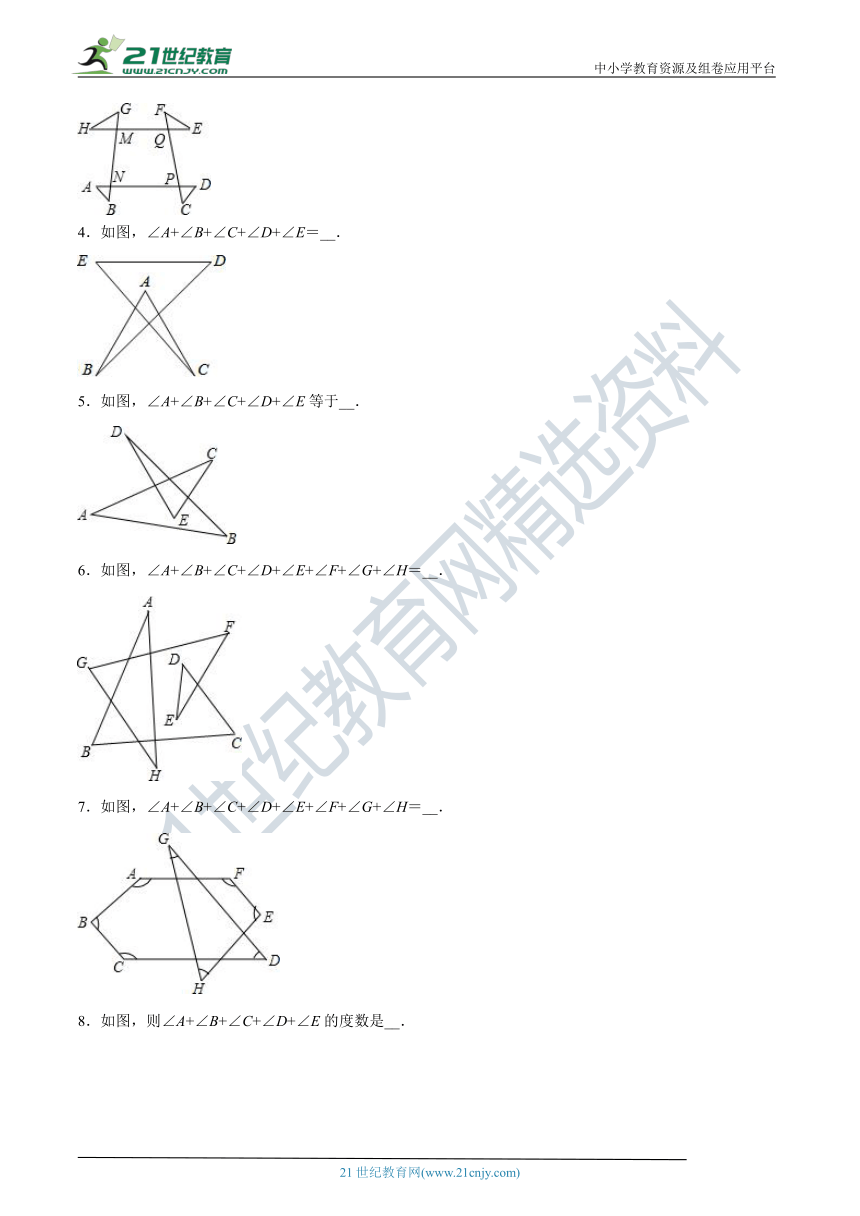
3.如右图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
4.如图,∠A+∠B+∠C+∠D+∠E=__.
5.如图,∠A+∠B+∠C+∠D+∠E等于__.
6.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
7.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
8.如图,则∠A+∠B+∠C+∠D+∠E的度数是__.
9.如图,在中,,,平分,平分,则______.
三、解答题
10.如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;www.21-cn-jy.com
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.21·世纪*教育网
11.如图,中,(1)若、的三等分线交于点、,请用表示、;(2)若、的等分线交于点、(、依次从下到上),请用表示,.21教育网
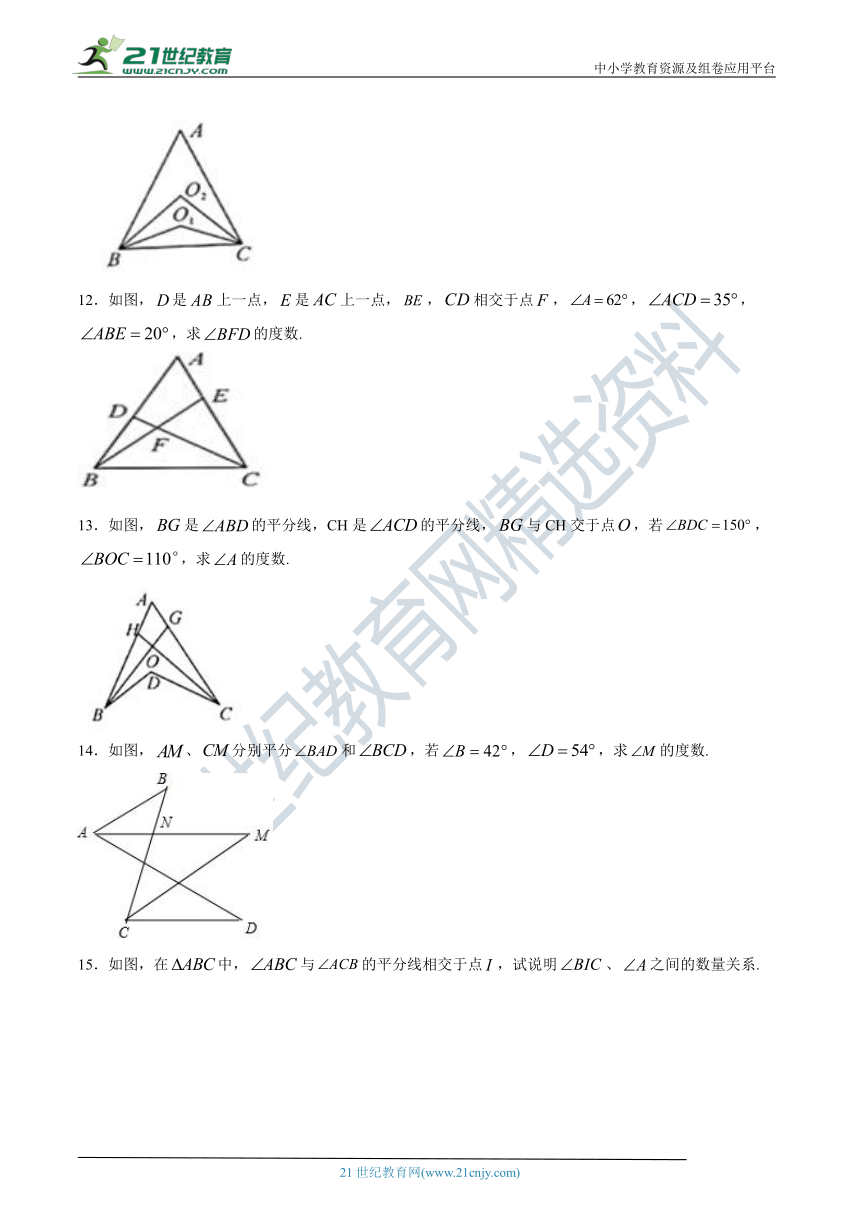
12.如图,是上一点,是上一点,,相交于点,,,,求的度数.
13.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
14.如图,、分别平分和,若,,求的度数.
15.如图,在中,与的平分线相交于点,试说明、之间的数量关系.
16.如图,已知分别交的边、于、,交的延长线于,,,,求的度数.
参考答案
1.B
【分析】在△ABC中利用三角形内角和定理可求出∠C的度数,由折叠的性质,可知:∠CDE=∠C′DE,∠CED=∠C′ED,结合∠2的度数可求出∠CED的度数,在△CDE中利用三角形内角和定理可求出∠CDE的度数,再由∠1=180°﹣∠CDE﹣∠C′DE即可求出结论.【出处:21教育名师】
解:在△ABC中,∠A=60°,∠B=70°,
∴∠C=180°﹣∠A﹣∠B=50°.
由折叠,可知:∠CDE=∠C′DE,∠CED=∠C′ED,
∴∠CED==99°,
∴∠CDE=180°﹣∠CED﹣∠C=31°,
∴∠1=180°﹣∠CDE﹣∠C′DE=180°﹣2∠CDE=118°.
故选:B.
【点拨】本题考查了三角形内角和定理以及折叠的性质,利用三角形内角和定理及折叠的性质求出∠CDE的度数是解题的关键.21*cnjy*com
2.B
【详解】
∵∠A=20°,∠ABC与∠ACB的角平分线交于D1,
∴∠D1BC+∠D1CB=(∠ABC+∠ACB)= (180°-∠A),
∴∠=180°- (180°-∠A)= ∠A+90°=100°,
同理:∠=60°,∠=40°,∠=30°,∠=25°.
故选B
3.360°
【分析】根据三角形的外角性质可得∠BNP=∠A+∠B,∠DPQ=∠C+∠D,∠FQM=∠E+∠F,∠HMN=∠G+∠H,再根据多边形的外角和定理即可求解.21教育名师原创作品
解:由图形可知:∠BNP=∠A+∠B,∠DPQ=∠C+∠D,∠FQM=∠E+∠F,∠HMN=∠G+∠H,
∵∠BNP+∠DPQ+∠FQM+∠HMN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠BNP+∠DPQ+∠FQM+∠HMN=360°.
故答案为:360°.
【点拨】本题考查了三角形的外角性质和多边形外角和等于360度,将∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的和转化为∠BNP+∠DPQ+∠FQM+∠HMN的和是解题的关键.www-2-1-cnjy-com
4.180°
【分析】先根据三角形外角的性质得出∠CFB=∠A+∠C,∠BGF=∠D+∠E,再由三角形内角和定理即可得出结论.
解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,
∴∠CFB=∠A+∠C,∠BGF=∠D+∠E,
∵∠B+∠CFB+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
【点拨】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
5.180°
【分析】根据三角形外角的性质可知∠B+∠A=∠1,∠D+∠E=∠2,再根据三角形内角和定理即可得出结论.
解:如图,
∵∠B+∠A=∠1,∠D+∠E=∠2,
∵∠1+∠2+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
【点拨】本题考查的是三角形外角的性质及三角形内角和定理,熟知“三角形的一个外角等于和它不相邻的两个内角的和”是解答此题的关键.
6.360°
【分析】连接CF,根据三角形的外角得到由三角形外角的性质可得:∠2=∠G+∠H,∠3=∠A+∠B,∠1=∠D+∠E=∠4+∠5,根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°.
解:如图,连接FC,
由三角形外角的性质可得:
∠2=∠G+∠H,
∠3=∠A+∠B,
∠1=∠D+∠E=∠4+∠5,
根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°
即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°,
故答案为360°.
【点拨】本题考查了三角形的内角与外角,解决本题的关键是熟记三角形的外角的性质.
7.720°
【分析】根据三角形的外角等于与它不相邻的两个内角的和,可得∠2与∠H、∠G的关系,∠1与∠2、∠D的关系,根据多边形的内角和公式,可得答案.21世纪教育网版权所有
解:如图:
由三角形的外角等于与它不相邻的两个内角的和,得
∠2=∠H+∠G,∠1=∠2+∠D,
∠1=∠H+∠G+∠D,
∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H
=∠A+∠B+∠C+∠E+∠F+∠H+∠G+∠D
=180°×(6-2)
=270°.
故答案为:720°.
【点拨】本题考查了多边形的内角与外角,先求出∠1=∠H+∠G+∠D,再求出多边形的内角和.
8.180°
【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠4=∠A+∠2,∠2=∠D+∠C,进而利用三角形的内角和定理求解.【来源:21·世纪·教育·网】
解:如图可知:
∵∠4是三角形的外角,
∴∠4=∠A+∠2,
同理∠2也是三角形的外角,
∴∠2=∠D+∠C,
在△BEG中,∵∠B+∠E+∠4=180°,
∴∠B+∠E+∠A+∠D+∠C=180°.
故答案为:180°.
【点拨】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.
9.
【分析】先根据角平分线的性质求出的度数,再利用三角形内角和定理即可求解.
解:∵平分,平分,
∴,
∴.
【点拨】本题考查了角平分线的性质及三角形内角和定理.熟练掌握三角形内角和定理是解题的关键.
10.(1)∠BDC=∠A+∠B+∠C,详见解析;(2)①40;②∠DCE=90°;③70
【分析】
(1)根据题意观察图形连接AD并延长至点F,根据一个三角形的外角等于与它不相邻的两个内角的和可证∠BDC=∠BDF+∠CDF;2·1·c·n·j·y
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值;
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=(∠ADB+∠AEB)+∠A,易得答案.
③由②方法,进而可得答案.
解:(1)连接AD并延长至点F,
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
∵∠BDC=∠BDF+∠CDF,
∴∠BDC=∠BAD+∠B+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD;
∴∠BDC=∠BAC +∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
∵∠A=50°,∠BXC=90°,
∴∠ABX+∠ACX=90°﹣50°=40°.
故答案是:40;
②由(1)的结论易得∠DBE=∠DAE +∠ADB+∠AEB,∠DCE=∠ADC+∠AEC+∠A
∵∠DAE=50°,∠DBE=130°,
∴∠ADB+∠AEB=80°;
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB
∴∠DCE=(∠ADB+∠AEB)+∠A=40°+50°=90°;
③由②知,∠BG1C=(∠ABD+∠ACD)+ ∠A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°﹣x°,
∴(140﹣x)+x=77,
∴14﹣x+x=77,
∴x=70,
∴∠A为70°.
故答案是:70.
【点拨】本题考查三角形外角的性质,三角形的内角和定理的应用,能求出∠BDC=∠A+∠B+∠C是解答的关键,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和.
11.(1),;(2),.
【分析】
(1)根据三角形内角和可得,再根据、的三等分线交于点、,可得然后根据三角形内角和定理即可用含表示、;【来源:21cnj*y.co*m】
(2)根据(1)中所体现的规律解答即可.
解:(1)∵,
∴,
∵、的三等分线交于点、,
∴
∴,
;
(2)由(1)可知,
.
【点拨】本题考查了三角形内角和定理及角的n等分线的性质.熟练应用三角形内角和定理求角的度数是解题的关键.【版权所有:21教育】
12..
【分析】根据三角形的外角性质先求出的度数,再利用三角形内角和定理即可注出的度数.
解:在△ADC中,
,
在在△BDF中,
.
【点拨】本题考查了三角形内角和定理及三角形外角的性质.熟练找出三角形内角与外角的关系是解题的关键.
13..
【分析】根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出2-1-c-n-j-y
解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点拨】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.21*cnjy*com
14..
【分析】根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系,代入数据进行计算即可得解;
解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=(∠B+∠D)=(42°+54°)=48°;
【点拨】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
15.,见解析.
【分析】根据角平分线的性质和三角形的内角和定理得出∠BIC=180°-(∠ABC+∠ACB)=180°-90°+∠A=90°+∠A,21cnjy.com
解:在中,∠ABC+∠ACB=180°-∠A
∵与的平分线相交于点,
∴,,
在中
.
【点拨】本题主要考查三角形内角和定理,以及角平分线的性质定理,熟练掌握相关的性质是解题的关键
16..
【分析】
根据三角形的内角和定理即可求解
解:在中,=--,
∴∠DEC=
【点拨】本题主要考查三角形内角和定理和外角的性质,掌握三角形内角和为180°及三角形的一个外角等于不相邻两个内角的和是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题11.9 三角形有关的角-燕尾模型(专项练习)
如图:这样的图形称之为“燕尾模型”
结论:∠BDC=∠A+∠B+∠C
一、单选题
1.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )21·cn·jy·com
A.50° B.118° C.100° D.90°
2.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.24° B.25° C.30° D.36°
二、填空题
3.如右图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
4.如图,∠A+∠B+∠C+∠D+∠E=__.
5.如图,∠A+∠B+∠C+∠D+∠E等于__.
6.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
7.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.
8.如图,则∠A+∠B+∠C+∠D+∠E的度数是__.
9.如图,在中,,,平分,平分,则______.
三、解答题
10.如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;www.21-cn-jy.com
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.21·世纪*教育网
11.如图,中,(1)若、的三等分线交于点、,请用表示、;(2)若、的等分线交于点、(、依次从下到上),请用表示,.21教育网
12.如图,是上一点,是上一点,,相交于点,,,,求的度数.
13.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
14.如图,、分别平分和,若,,求的度数.
15.如图,在中,与的平分线相交于点,试说明、之间的数量关系.
16.如图,已知分别交的边、于、,交的延长线于,,,,求的度数.
参考答案
1.B
【分析】在△ABC中利用三角形内角和定理可求出∠C的度数,由折叠的性质,可知:∠CDE=∠C′DE,∠CED=∠C′ED,结合∠2的度数可求出∠CED的度数,在△CDE中利用三角形内角和定理可求出∠CDE的度数,再由∠1=180°﹣∠CDE﹣∠C′DE即可求出结论.【出处:21教育名师】
解:在△ABC中,∠A=60°,∠B=70°,
∴∠C=180°﹣∠A﹣∠B=50°.
由折叠,可知:∠CDE=∠C′DE,∠CED=∠C′ED,
∴∠CED==99°,
∴∠CDE=180°﹣∠CED﹣∠C=31°,
∴∠1=180°﹣∠CDE﹣∠C′DE=180°﹣2∠CDE=118°.
故选:B.
【点拨】本题考查了三角形内角和定理以及折叠的性质,利用三角形内角和定理及折叠的性质求出∠CDE的度数是解题的关键.21*cnjy*com
2.B
【详解】
∵∠A=20°,∠ABC与∠ACB的角平分线交于D1,
∴∠D1BC+∠D1CB=(∠ABC+∠ACB)= (180°-∠A),
∴∠=180°- (180°-∠A)= ∠A+90°=100°,
同理:∠=60°,∠=40°,∠=30°,∠=25°.
故选B
3.360°
【分析】根据三角形的外角性质可得∠BNP=∠A+∠B,∠DPQ=∠C+∠D,∠FQM=∠E+∠F,∠HMN=∠G+∠H,再根据多边形的外角和定理即可求解.21教育名师原创作品
解:由图形可知:∠BNP=∠A+∠B,∠DPQ=∠C+∠D,∠FQM=∠E+∠F,∠HMN=∠G+∠H,
∵∠BNP+∠DPQ+∠FQM+∠HMN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠BNP+∠DPQ+∠FQM+∠HMN=360°.
故答案为:360°.
【点拨】本题考查了三角形的外角性质和多边形外角和等于360度,将∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的和转化为∠BNP+∠DPQ+∠FQM+∠HMN的和是解题的关键.www-2-1-cnjy-com
4.180°
【分析】先根据三角形外角的性质得出∠CFB=∠A+∠C,∠BGF=∠D+∠E,再由三角形内角和定理即可得出结论.
解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,
∴∠CFB=∠A+∠C,∠BGF=∠D+∠E,
∵∠B+∠CFB+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
【点拨】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
5.180°
【分析】根据三角形外角的性质可知∠B+∠A=∠1,∠D+∠E=∠2,再根据三角形内角和定理即可得出结论.
解:如图,
∵∠B+∠A=∠1,∠D+∠E=∠2,
∵∠1+∠2+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
【点拨】本题考查的是三角形外角的性质及三角形内角和定理,熟知“三角形的一个外角等于和它不相邻的两个内角的和”是解答此题的关键.
6.360°
【分析】连接CF,根据三角形的外角得到由三角形外角的性质可得:∠2=∠G+∠H,∠3=∠A+∠B,∠1=∠D+∠E=∠4+∠5,根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°.
解:如图,连接FC,
由三角形外角的性质可得:
∠2=∠G+∠H,
∠3=∠A+∠B,
∠1=∠D+∠E=∠4+∠5,
根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°
即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°,
故答案为360°.
【点拨】本题考查了三角形的内角与外角,解决本题的关键是熟记三角形的外角的性质.
7.720°
【分析】根据三角形的外角等于与它不相邻的两个内角的和,可得∠2与∠H、∠G的关系,∠1与∠2、∠D的关系,根据多边形的内角和公式,可得答案.21世纪教育网版权所有
解:如图:
由三角形的外角等于与它不相邻的两个内角的和,得
∠2=∠H+∠G,∠1=∠2+∠D,
∠1=∠H+∠G+∠D,
∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H
=∠A+∠B+∠C+∠E+∠F+∠H+∠G+∠D
=180°×(6-2)
=270°.
故答案为:720°.
【点拨】本题考查了多边形的内角与外角,先求出∠1=∠H+∠G+∠D,再求出多边形的内角和.
8.180°
【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠4=∠A+∠2,∠2=∠D+∠C,进而利用三角形的内角和定理求解.【来源:21·世纪·教育·网】
解:如图可知:
∵∠4是三角形的外角,
∴∠4=∠A+∠2,
同理∠2也是三角形的外角,
∴∠2=∠D+∠C,
在△BEG中,∵∠B+∠E+∠4=180°,
∴∠B+∠E+∠A+∠D+∠C=180°.
故答案为:180°.
【点拨】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.
9.
【分析】先根据角平分线的性质求出的度数,再利用三角形内角和定理即可求解.
解:∵平分,平分,
∴,
∴.
【点拨】本题考查了角平分线的性质及三角形内角和定理.熟练掌握三角形内角和定理是解题的关键.
10.(1)∠BDC=∠A+∠B+∠C,详见解析;(2)①40;②∠DCE=90°;③70
【分析】
(1)根据题意观察图形连接AD并延长至点F,根据一个三角形的外角等于与它不相邻的两个内角的和可证∠BDC=∠BDF+∠CDF;2·1·c·n·j·y
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值;
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=(∠ADB+∠AEB)+∠A,易得答案.
③由②方法,进而可得答案.
解:(1)连接AD并延长至点F,
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
∵∠BDC=∠BDF+∠CDF,
∴∠BDC=∠BAD+∠B+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD;
∴∠BDC=∠BAC +∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
∵∠A=50°,∠BXC=90°,
∴∠ABX+∠ACX=90°﹣50°=40°.
故答案是:40;
②由(1)的结论易得∠DBE=∠DAE +∠ADB+∠AEB,∠DCE=∠ADC+∠AEC+∠A
∵∠DAE=50°,∠DBE=130°,
∴∠ADB+∠AEB=80°;
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB
∴∠DCE=(∠ADB+∠AEB)+∠A=40°+50°=90°;
③由②知,∠BG1C=(∠ABD+∠ACD)+ ∠A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°﹣x°,
∴(140﹣x)+x=77,
∴14﹣x+x=77,
∴x=70,
∴∠A为70°.
故答案是:70.
【点拨】本题考查三角形外角的性质,三角形的内角和定理的应用,能求出∠BDC=∠A+∠B+∠C是解答的关键,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和.
11.(1),;(2),.
【分析】
(1)根据三角形内角和可得,再根据、的三等分线交于点、,可得然后根据三角形内角和定理即可用含表示、;【来源:21cnj*y.co*m】
(2)根据(1)中所体现的规律解答即可.
解:(1)∵,
∴,
∵、的三等分线交于点、,
∴
∴,
;
(2)由(1)可知,
.
【点拨】本题考查了三角形内角和定理及角的n等分线的性质.熟练应用三角形内角和定理求角的度数是解题的关键.【版权所有:21教育】
12..
【分析】根据三角形的外角性质先求出的度数,再利用三角形内角和定理即可注出的度数.
解:在△ADC中,
,
在在△BDF中,
.
【点拨】本题考查了三角形内角和定理及三角形外角的性质.熟练找出三角形内角与外角的关系是解题的关键.
13..
【分析】根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出2-1-c-n-j-y
解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点拨】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.21*cnjy*com
14..
【分析】根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系,代入数据进行计算即可得解;
解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=(∠B+∠D)=(42°+54°)=48°;
【点拨】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
15.,见解析.
【分析】根据角平分线的性质和三角形的内角和定理得出∠BIC=180°-(∠ABC+∠ACB)=180°-90°+∠A=90°+∠A,21cnjy.com
解:在中,∠ABC+∠ACB=180°-∠A
∵与的平分线相交于点,
∴,,
在中
.
【点拨】本题主要考查三角形内角和定理,以及角平分线的性质定理,熟练掌握相关的性质是解题的关键
16..
【分析】
根据三角形的内角和定理即可求解
解:在中,=--,
∴∠DEC=
【点拨】本题主要考查三角形内角和定理和外角的性质,掌握三角形内角和为180°及三角形的一个外角等于不相邻两个内角的和是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
