华东师大版七上数学 2.7有理数的减法 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七上数学 2.7有理数的减法 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 789.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 19:44:33 | ||
图片预览





文档简介
(共16张PPT)
7 有理数的减法
第二章 有理数及其运算
学习目标
1.理解、掌握有理数的减法法则,会将有理数的减
法运算转化为加法运算.(重点、难点)
2.通过把有理数的减法运算转化为加法运算,渗透
转化思想,培养运算能力.
导入新课
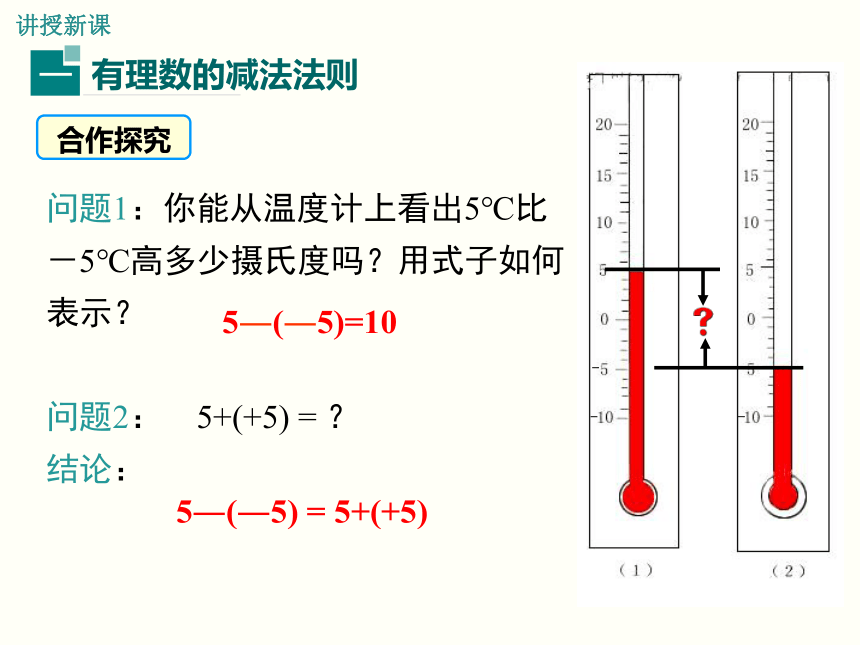
你听说过国家级森林公园抱犊崮吗?已知某日抱犊崮山下温度为5 ℃,山上温度为-5 ℃,你能列式表示出山上温度与山下温度的温差吗?
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2: 5+(+5) = ?
结论:
讲授新课
有理数的减法法则
一
合作探究
5―(―5)=10
5―(―5) = 5+(+5)
试一试:请根据提供的式子完成下列算式
(-3)+(+10)= +7
( –2 )+ (–8)=-10
②(–10)–(–8)=
①(+7)-(+10)=
-3
-2
③(+7)+(-10)=
④(–10)+(+8)=
-3
-2
思考:算式①和②是什么运算?等式③和④是又是什么运算?结果怎样?
议一议:这两个等式有什么特点?从等式中同学们
对减法运算有什么认识?
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
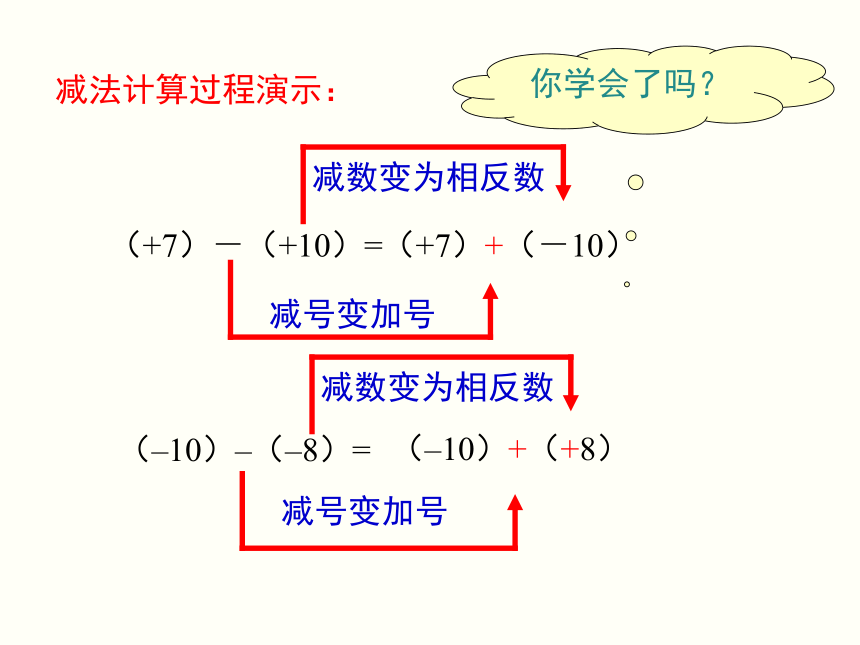
减法计算过程演示:
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减号变加号
减数变为相反数
减数变为相反数
减号变加号
你学会了吗?
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b = a + (-b)
减号变加号
减数变其相反数
被减数不变
归纳总结
下列括号内各应填什么数?
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( )
练一练
3
4
3
-39
总结:
1.任何数减零仍得原数;
2.零减去一个数等于这个数的相反数.
(1)0 –8= (2)(-5 )– 0=
(3)30 – 0 = (4)0 – (–15) =
– 8
15
– 5
30
(1)(-3)―(―5); (2)0-7;
(3)7.2―(―4.8); (4)-3―(+6) .
例1 计算:
典例精析
1.计算(口答):
(1)6-9; (2)(+4)-(-7);
(3)(-5)-(-8) ; (4)(-4)-9;
(5)0-(-5); (6)0-5.
练一练
答案:(1)-3
(2)11
(3)3
(4)-13
(5)5
(6)-5
3.判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大( )
(2)两个数相减,被减数一定比减数大( )
(3)两数之差一定小于被减数( )
(4)0减去任何数,差都为负数( )
(5)较大的数减去较小的数,差一定是正数( )
√
×
×
×
×
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度是 8848 米,吐鲁番盆地的海拔高度是–155 米,两处高度相差多少米?
解:8848-(-155)
=8848+155
=9003(米)
答:两处高度相差9003米.
议一议:在运用有理数的减法解决实际问题的过程中,通常需要经历哪些步骤?
【小结】有理数减法在实际应用中的四个步骤:
1.审:审清题意;
2.列:列出正确的算式;
3.算:按照减法运算法则,进行正确的计算;
4.答:写出实际问题的答案.
课堂小结
有理数减法法则
a-b = a +(-b)
一般法则
应用
特殊法则
0-b =-b;b-0 =b
7 有理数的减法
第二章 有理数及其运算
学习目标
1.理解、掌握有理数的减法法则,会将有理数的减
法运算转化为加法运算.(重点、难点)
2.通过把有理数的减法运算转化为加法运算,渗透
转化思想,培养运算能力.
导入新课
你听说过国家级森林公园抱犊崮吗?已知某日抱犊崮山下温度为5 ℃,山上温度为-5 ℃,你能列式表示出山上温度与山下温度的温差吗?
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2: 5+(+5) = ?
结论:
讲授新课
有理数的减法法则
一
合作探究
5―(―5)=10
5―(―5) = 5+(+5)
试一试:请根据提供的式子完成下列算式
(-3)+(+10)= +7
( –2 )+ (–8)=-10
②(–10)–(–8)=
①(+7)-(+10)=
-3
-2
③(+7)+(-10)=
④(–10)+(+8)=
-3
-2
思考:算式①和②是什么运算?等式③和④是又是什么运算?结果怎样?
议一议:这两个等式有什么特点?从等式中同学们
对减法运算有什么认识?
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减法计算过程演示:
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减号变加号
减数变为相反数
减数变为相反数
减号变加号
你学会了吗?
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b = a + (-b)
减号变加号
减数变其相反数
被减数不变
归纳总结
下列括号内各应填什么数?
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( )
练一练
3
4
3
-39
总结:
1.任何数减零仍得原数;
2.零减去一个数等于这个数的相反数.
(1)0 –8= (2)(-5 )– 0=
(3)30 – 0 = (4)0 – (–15) =
– 8
15
– 5
30
(1)(-3)―(―5); (2)0-7;
(3)7.2―(―4.8); (4)-3―(+6) .
例1 计算:
典例精析
1.计算(口答):
(1)6-9; (2)(+4)-(-7);
(3)(-5)-(-8) ; (4)(-4)-9;
(5)0-(-5); (6)0-5.
练一练
答案:(1)-3
(2)11
(3)3
(4)-13
(5)5
(6)-5
3.判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大( )
(2)两个数相减,被减数一定比减数大( )
(3)两数之差一定小于被减数( )
(4)0减去任何数,差都为负数( )
(5)较大的数减去较小的数,差一定是正数( )
√
×
×
×
×
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度是 8848 米,吐鲁番盆地的海拔高度是–155 米,两处高度相差多少米?
解:8848-(-155)
=8848+155
=9003(米)
答:两处高度相差9003米.
议一议:在运用有理数的减法解决实际问题的过程中,通常需要经历哪些步骤?
【小结】有理数减法在实际应用中的四个步骤:
1.审:审清题意;
2.列:列出正确的算式;
3.算:按照减法运算法则,进行正确的计算;
4.答:写出实际问题的答案.
课堂小结
有理数减法法则
a-b = a +(-b)
一般法则
应用
特殊法则
0-b =-b;b-0 =b
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
