2021-2022学年北师大版九年级数学上册4.7相似三角形的性质 专项训练A(word版、含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.7相似三角形的性质 专项训练A(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 622.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 20:54:31 | ||
图片预览


文档简介
4.7相似三角形的性质 专项训练A
姓名:___________班级:___________
一、选择题
1.如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )
A.9 B.6 C.3 D.4
2.下列语句正确的是( )
A.一条线段的黄金分割点有且只有一个
B.三角形三条中线的交点叫做三角形的重心,三角形的重心到一个顶点的距离等于它到中点距离的两倍
C.两边对应成比例且有一角对应相等的两个三角形相似
D.相似三角形所有对应线段(对应角平分线、对应中线、对应高)的比等于相似比,面积比是相似比的平方
3.如图,在梯形ABCD中,ADBC,BC=2AD.如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
A.S1=S3 B.S2=2S4 C.S2=2S1 D.S1 S3=S2 S4
4.顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”,它的底与腰的比值为黄金比.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为( )
A. B. C. D.
5.如图,在矩形中,,,平分,与对角线相交于点,是线段的中点,则为( )
B. C. D.
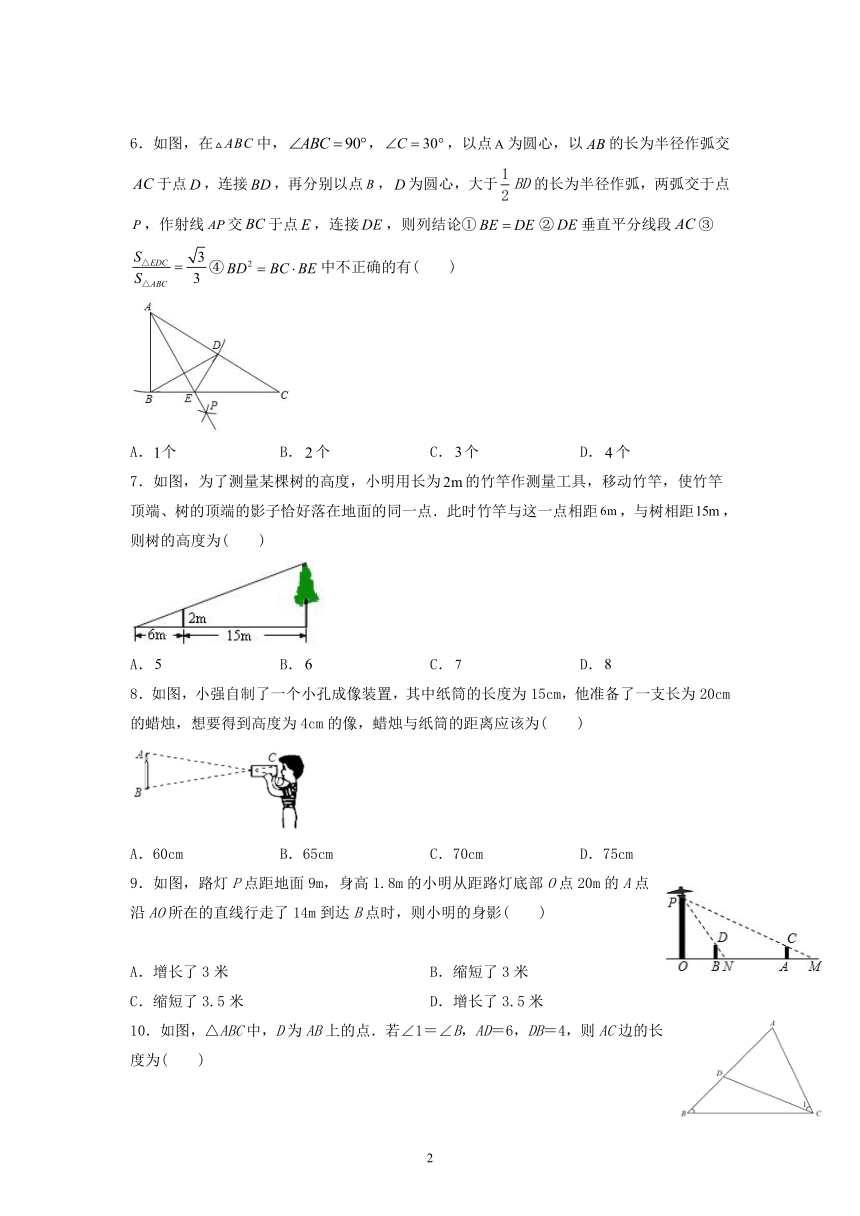
6.如图,在中,,,以点为圆心,以的长为半径作弧交于点,连接,再分别以点,为圆心,大于的长为半径作弧,两弧交于点,作射线交于点,连接,则列结论①②垂直平分线段③④中不正确的有( )
A.个 B.个 C.个 D.个
7.如图,为了测量某棵树的高度,小明用长为的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距,与树相距,则树的高度为( )
A. B. C. D.
8.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为4cm的像,蜡烛与纸筒的距离应该为( )
A.60cm B.65cm C.70cm D.75cm
9.如图,路灯P点距地面9m,身高1.8m的小明从距路灯底部O点20m的A点沿AO所在的直线行走了14m到达B点时,则小明的身影( )
A.增长了3米 B.缩短了3米
C.缩短了3.5米 D.增长了3.5米
10.如图,△ABC中,D为AB上的点.若∠1=∠B,AD=6,DB=4,则AC边的长度为( )
A.5 B.2 C.2 D.2
11.如图,AB∥DC,AD与BC的交点为M,过点M作MH∥AB交BD于H.已知AB=3,MH=2,则△ABM与△MCD的面积之比为( )
A.1:2 B.1:4 C.2:3 D.4:9
12.如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB边上一动点,连接PC、PE,若PAE与PBC是相似三角形,则满足条件的点P的数量为( )
A.1个 B.2个 C.3个 D.4个
13.如图,平行四边形ABCD中,EF//AB,DE:EA=2:3,EF=6,则CD的长为( )
A.15 B.10 C.8 D.16
14.如图,在矩形ABCD中,AB=3,BC=4,点P在AD上,若将△ABP沿BP折叠,使点A落在矩形对角线AC上,则AA′的长为( )
A. B. C. D.
15.如图,正方形中,,点E在边上,且.将沿对折至,延长交于点G,连结.下列结论:①;②;③ ;④ .其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
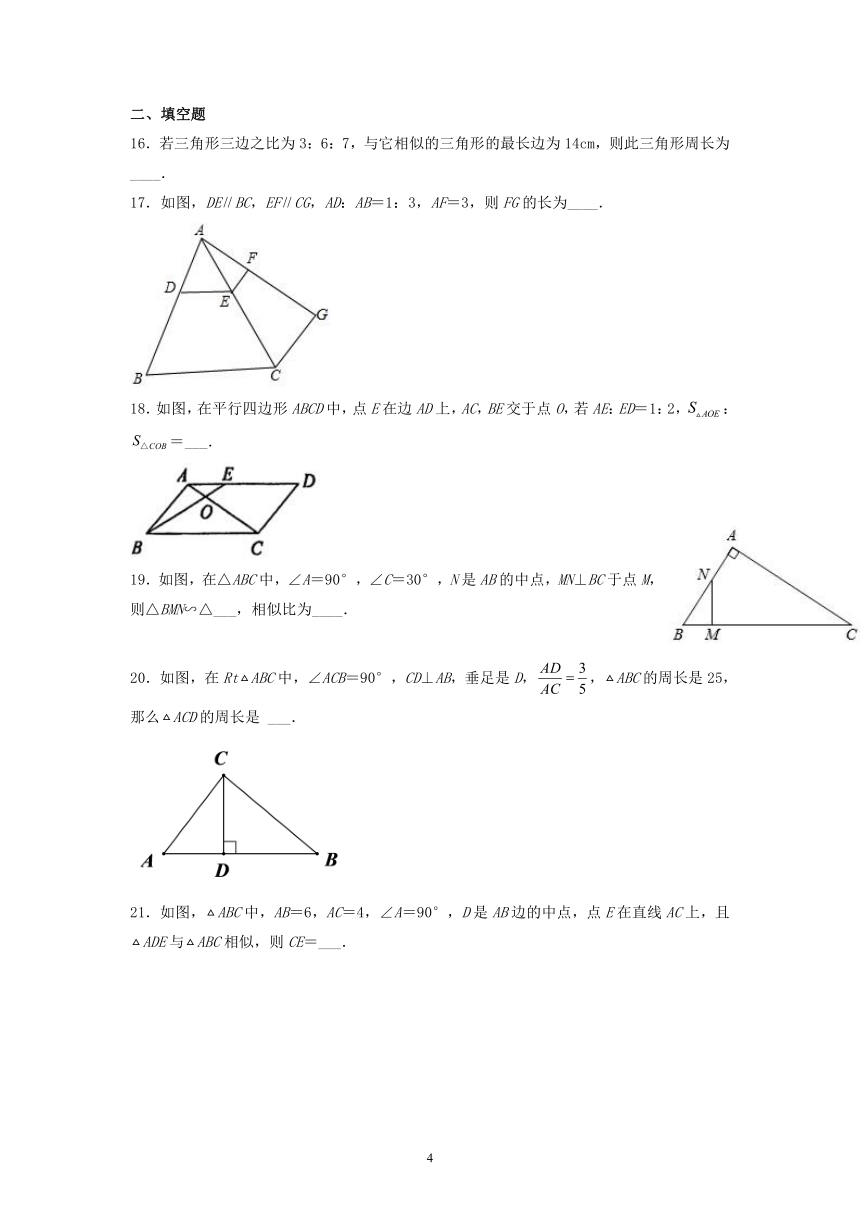
16.若三角形三边之比为3:6:7,与它相似的三角形的最长边为14cm,则此三角形周长为____.
17.如图,DEBC,EFCG,AD:AB=1:3,AF=3,则FG的长为____.
18.如图,在平行四边形ABCD中,点E在边AD上,AC,BE交于点O,若AE:ED=1:2,:=___.
19.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△___,相似比为____.
20.如图,在RtABC中,∠ACB=90°,CD⊥AB,垂足是D,,ABC的周长是25,那么ACD的周长是 ___.
21.如图,ABC中,AB=6,AC=4,∠A=90°,D是AB边的中点,点E在直线AC上,且ADE与ABC相似,则CE=___.
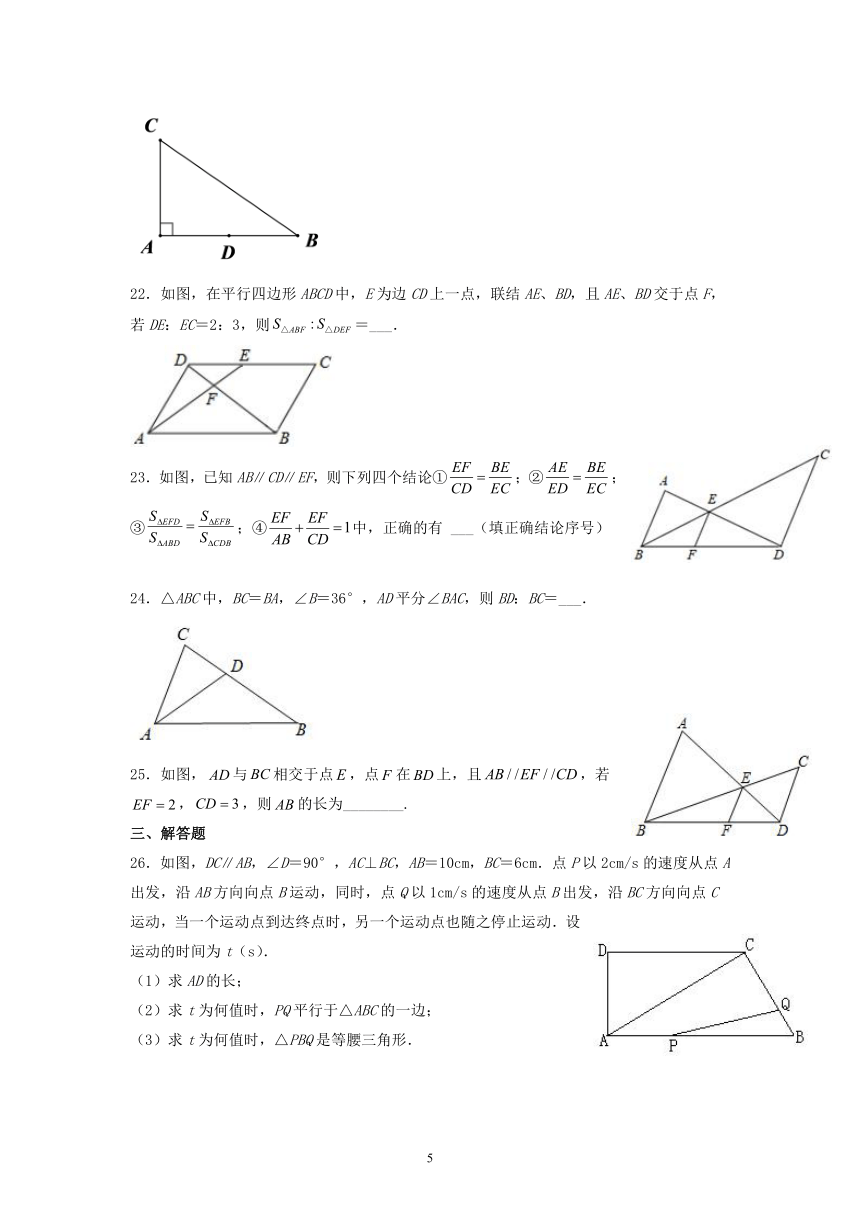
22.如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则=___.
23.如图,已知AB∥CD∥EF,则下列四个结论①;②;③;④中,正确的有 ___(填正确结论序号)
24.△ABC中,BC=BA,∠B=36°,AD平分∠BAC,则BD:BC=___.
25.如图,与相交于点,点在上,且,若 ,,则的长为________.
三、解答题
26.如图,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,BC=6cm.点P以2cm/s的速度从点A出发,沿AB方向向点B运动,同时,点Q以1cm/s的速度从点B出发,沿BC方向向点C运动,当一个运动点到达终点时,另一个运动点也随之停止运动.设运动的时间为t(s).
(1)求AD的长;
(2)求t为何值时,PQ平行于△ABC的一边;
(3)求t为何值时,△PBQ是等腰三角形.
27.如图,在△ABC中,,是△ABC的高,连接.
(1)求证:△ADE∽△ABC;
(2)若,,求的长.
28.如图,边长为的正方形中,点为的中点,连接,将沿折叠得到,交于点,连接、.
(1)判断与的关系,并给予证明;
(2)求的长.
29.已知:如图,点D、F在△ABC的边AB上,点E在边AC上,且DEBC.
(1)若AB=6,BC=4,BD=2,求DE的长;
(2)若,求证:EFDC.
30.如图,中,是边上的高,,.作矩形,使它的一边在上,顶点,分别在,上,与的交点为,且矩形长是宽的倍.
(1)求证:;
(2)试求矩形的周长.
参考答案
1-5:ADBDD 6-10:ACDCD 11-15:BCACD
16.32cm 17.6 18.1 19.BAC 1:4 20.
21.或或 22. 23.②④ 24. 25.
26.解:(1)过C作CE⊥AB于E,
∵DC∥AB, ∴CE⊥CD,∵∠D=90°,∴AD⊥CD,∴AD∥CE,DC∥AE,∴四边形ADCE为平四边形,
∵∠D=90°,∴四边形ADCE为矩形,∴AD=EC,∵AC⊥BC,AB=10cm,BC=6cm.
∴AC=,∴,∴,
∴AD=;
(2)∵PQ∥AC,∴∠CAB=∠QPB,∠ACB=∠PQB∴△ABC∽△PBQ,∴,
∵点P以2cm/s的速度从点A出发,沿AB方向向点B运动,同时,点Q以1cm/s的速度从点B出发,沿BC方向向点C运动,运动的时间为t(s).
∴AP=2t,BQ=t,PB=10-2t,∴∴ 解方程得
经检验符合要求,
∴时,PQ平行于△ABC的一边;
(3)△PBQ是等腰三角形分三种情况,当QP=BQ时,过Q作QF⊥PB于F,
∴PB=2PF,∵CE⊥AB,QF⊥PB,∴CE∥QF,∴
在Rt△CEB中,BE=,
∴,∴,∴10-2t=∴;
当PB=PQ时,即10-2t=t∴;
当PB=BQ,过P作PG⊥BQ于G,
∴QG=BG=
∵∠PGB=∠ACB=90°,∠PBG=∠ABC,
∴△PBG∽△ABC
∴,即
解得,
∵0<t≤5,,
t为或或时,△PBQ是等腰三角形.
27.(1)证明:∵BD,CE是△ABC的高,
∴∠ADB=∠AEC=90°,∵∠A=∠A,∴△ABD∽△ACE. ,,
∵,;
(2)∵
,,则,,又,,
.
28.(1)垂直平分,证明如下:
将沿折叠得到,,,垂直平分;
(2)解:延长交于,连接.
四边形是正方形,,,,
,
由翻折的性质可知,,,,
点是的中点,,,在和中,
,,
,,,,
,,,,
,,,
,,.
29.,,,,即,
解得;
(2),,,,
又,,,.
30.(1)证明:四边形为矩形,,而,,
,;
(2)解:设,,则,解得,这个矩形的周长;
姓名:___________班级:___________
一、选择题
1.如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )
A.9 B.6 C.3 D.4
2.下列语句正确的是( )
A.一条线段的黄金分割点有且只有一个
B.三角形三条中线的交点叫做三角形的重心,三角形的重心到一个顶点的距离等于它到中点距离的两倍
C.两边对应成比例且有一角对应相等的两个三角形相似
D.相似三角形所有对应线段(对应角平分线、对应中线、对应高)的比等于相似比,面积比是相似比的平方
3.如图,在梯形ABCD中,ADBC,BC=2AD.如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
A.S1=S3 B.S2=2S4 C.S2=2S1 D.S1 S3=S2 S4
4.顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”,它的底与腰的比值为黄金比.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为( )
A. B. C. D.
5.如图,在矩形中,,,平分,与对角线相交于点,是线段的中点,则为( )
B. C. D.
6.如图,在中,,,以点为圆心,以的长为半径作弧交于点,连接,再分别以点,为圆心,大于的长为半径作弧,两弧交于点,作射线交于点,连接,则列结论①②垂直平分线段③④中不正确的有( )
A.个 B.个 C.个 D.个
7.如图,为了测量某棵树的高度,小明用长为的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距,与树相距,则树的高度为( )
A. B. C. D.
8.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为4cm的像,蜡烛与纸筒的距离应该为( )
A.60cm B.65cm C.70cm D.75cm
9.如图,路灯P点距地面9m,身高1.8m的小明从距路灯底部O点20m的A点沿AO所在的直线行走了14m到达B点时,则小明的身影( )
A.增长了3米 B.缩短了3米
C.缩短了3.5米 D.增长了3.5米
10.如图,△ABC中,D为AB上的点.若∠1=∠B,AD=6,DB=4,则AC边的长度为( )
A.5 B.2 C.2 D.2
11.如图,AB∥DC,AD与BC的交点为M,过点M作MH∥AB交BD于H.已知AB=3,MH=2,则△ABM与△MCD的面积之比为( )
A.1:2 B.1:4 C.2:3 D.4:9
12.如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB边上一动点,连接PC、PE,若PAE与PBC是相似三角形,则满足条件的点P的数量为( )
A.1个 B.2个 C.3个 D.4个
13.如图,平行四边形ABCD中,EF//AB,DE:EA=2:3,EF=6,则CD的长为( )
A.15 B.10 C.8 D.16
14.如图,在矩形ABCD中,AB=3,BC=4,点P在AD上,若将△ABP沿BP折叠,使点A落在矩形对角线AC上,则AA′的长为( )
A. B. C. D.
15.如图,正方形中,,点E在边上,且.将沿对折至,延长交于点G,连结.下列结论:①;②;③ ;④ .其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
16.若三角形三边之比为3:6:7,与它相似的三角形的最长边为14cm,则此三角形周长为____.
17.如图,DEBC,EFCG,AD:AB=1:3,AF=3,则FG的长为____.
18.如图,在平行四边形ABCD中,点E在边AD上,AC,BE交于点O,若AE:ED=1:2,:=___.
19.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△___,相似比为____.
20.如图,在RtABC中,∠ACB=90°,CD⊥AB,垂足是D,,ABC的周长是25,那么ACD的周长是 ___.
21.如图,ABC中,AB=6,AC=4,∠A=90°,D是AB边的中点,点E在直线AC上,且ADE与ABC相似,则CE=___.
22.如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则=___.
23.如图,已知AB∥CD∥EF,则下列四个结论①;②;③;④中,正确的有 ___(填正确结论序号)
24.△ABC中,BC=BA,∠B=36°,AD平分∠BAC,则BD:BC=___.
25.如图,与相交于点,点在上,且,若 ,,则的长为________.
三、解答题
26.如图,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,BC=6cm.点P以2cm/s的速度从点A出发,沿AB方向向点B运动,同时,点Q以1cm/s的速度从点B出发,沿BC方向向点C运动,当一个运动点到达终点时,另一个运动点也随之停止运动.设运动的时间为t(s).
(1)求AD的长;
(2)求t为何值时,PQ平行于△ABC的一边;
(3)求t为何值时,△PBQ是等腰三角形.
27.如图,在△ABC中,,是△ABC的高,连接.
(1)求证:△ADE∽△ABC;
(2)若,,求的长.
28.如图,边长为的正方形中,点为的中点,连接,将沿折叠得到,交于点,连接、.
(1)判断与的关系,并给予证明;
(2)求的长.
29.已知:如图,点D、F在△ABC的边AB上,点E在边AC上,且DEBC.
(1)若AB=6,BC=4,BD=2,求DE的长;
(2)若,求证:EFDC.
30.如图,中,是边上的高,,.作矩形,使它的一边在上,顶点,分别在,上,与的交点为,且矩形长是宽的倍.
(1)求证:;
(2)试求矩形的周长.
参考答案
1-5:ADBDD 6-10:ACDCD 11-15:BCACD
16.32cm 17.6 18.1 19.BAC 1:4 20.
21.或或 22. 23.②④ 24. 25.
26.解:(1)过C作CE⊥AB于E,
∵DC∥AB, ∴CE⊥CD,∵∠D=90°,∴AD⊥CD,∴AD∥CE,DC∥AE,∴四边形ADCE为平四边形,
∵∠D=90°,∴四边形ADCE为矩形,∴AD=EC,∵AC⊥BC,AB=10cm,BC=6cm.
∴AC=,∴,∴,
∴AD=;
(2)∵PQ∥AC,∴∠CAB=∠QPB,∠ACB=∠PQB∴△ABC∽△PBQ,∴,
∵点P以2cm/s的速度从点A出发,沿AB方向向点B运动,同时,点Q以1cm/s的速度从点B出发,沿BC方向向点C运动,运动的时间为t(s).
∴AP=2t,BQ=t,PB=10-2t,∴∴ 解方程得
经检验符合要求,
∴时,PQ平行于△ABC的一边;
(3)△PBQ是等腰三角形分三种情况,当QP=BQ时,过Q作QF⊥PB于F,
∴PB=2PF,∵CE⊥AB,QF⊥PB,∴CE∥QF,∴
在Rt△CEB中,BE=,
∴,∴,∴10-2t=∴;
当PB=PQ时,即10-2t=t∴;
当PB=BQ,过P作PG⊥BQ于G,
∴QG=BG=
∵∠PGB=∠ACB=90°,∠PBG=∠ABC,
∴△PBG∽△ABC
∴,即
解得,
∵0<t≤5,,
t为或或时,△PBQ是等腰三角形.
27.(1)证明:∵BD,CE是△ABC的高,
∴∠ADB=∠AEC=90°,∵∠A=∠A,∴△ABD∽△ACE. ,,
∵,;
(2)∵
,,则,,又,,
.
28.(1)垂直平分,证明如下:
将沿折叠得到,,,垂直平分;
(2)解:延长交于,连接.
四边形是正方形,,,,
,
由翻折的性质可知,,,,
点是的中点,,,在和中,
,,
,,,,
,,,,
,,,
,,.
29.,,,,即,
解得;
(2),,,,
又,,,.
30.(1)证明:四边形为矩形,,而,,
,;
(2)解:设,,则,解得,这个矩形的周长;
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
