5.1 平行四边形的性质同步练习(含答案)
文档属性
| 名称 | 5.1 平行四边形的性质同步练习(含答案) | 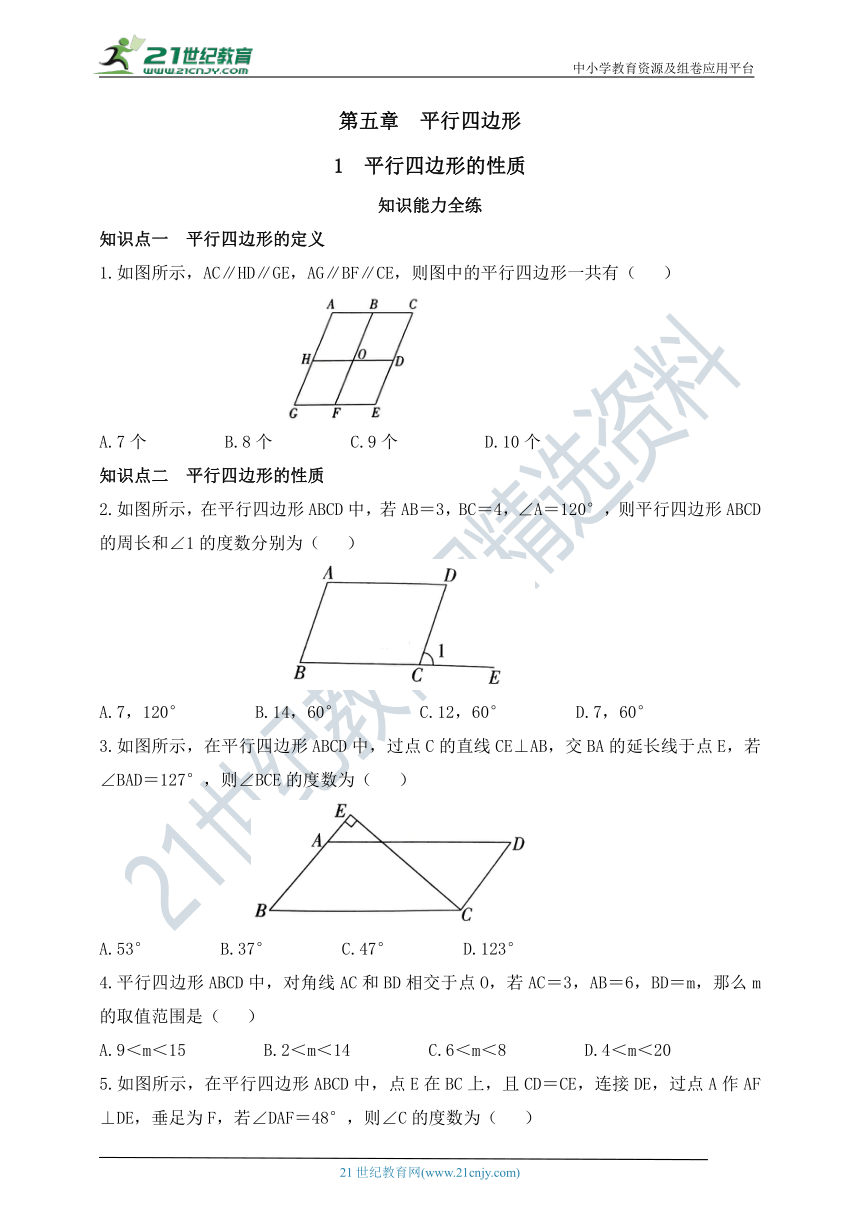 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:10:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
1 平行四边形的性质
知识能力全练
知识点一 平行四边形的定义
1.如图所示,AC∥HD∥GE,AG∥BF∥CE,则图中的平行四边形一共有( )
A.7个 B.8个 C.9个 D.10个
知识点二 平行四边形的性质
2.如图所示,在平行四边形ABCD中,若AB=3,BC=4,∠A=120°,则平行四边形ABCD的周长和∠1的度数分别为( )
A.7,120° B.14,60° C.12,60° D.7,60°
3.如图所示,在平行四边形ABCD中,过点C的直线CE⊥AB,交BA的延长线于点E,若∠BAD=127°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
4.平行四边形ABCD中,对角线AC和BD相交于点O,若AC=3,AB=6,BD=m,那么m的取值范围是( )
A.9<m<15 B.2<m<14 C.6<m<8 D.4<m<20
5.如图所示,在平行四边形ABCD中,点E在BC上,且CD=CE,连接DE,过点A作AF⊥DE,垂足为F,若∠DAF=48°,则∠C的度数为( )
A.84° B.96° C.98° D.106°
6.在平行四边形ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,若EF=2,则AB的长为( )
A.3 B.5 C.2或3 D.3或5
7.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
A. B.2 C. D.
8.如图所示,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
9.如图所示,平行四边形ABCD的对角线AC、BD交于点0,AC⊥BC,AC=10,BD=26.
(1)求BC的长;
(2)求平行四边形ABCD的面积.
知识点三 两条平行线间的距离
10.已知平行四边形两邻边长分别为16,20,若两条长边之间的距离为8,则两条短边之间的距离为( )
A.4 B.5 C.10 D.8
11.如图所示,已知四边形ABCD的面积为S,请画出一个与四边形ABCD面积相等的三角形,并说明理由.
巩固提高全练
12.平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.4:3:3:4 B.7:5:5:7 C.4:3:2:1 D.7:5:7:5
13.如图所示,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B=( )
A.124° B.114° C.104° D.66°
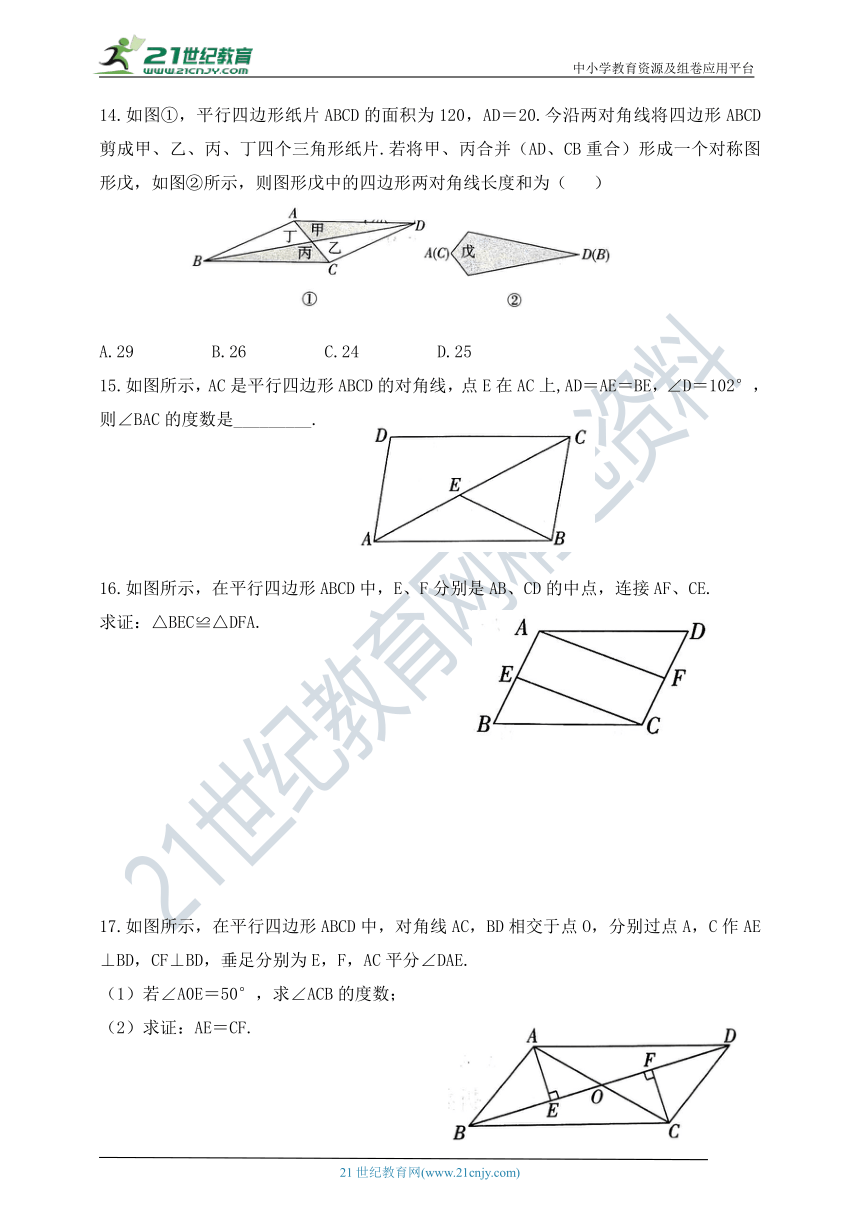
14.如图①,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一个对称图形戊,如图②所示,则图形戊中的四边形两对角线长度和为( )
A.29 B.26 C.24 D.25
15.如图所示,AC是平行四边形ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是_________.
16.如图所示,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
求证:△BEC≌△DFA.
17.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F,AC平分∠DAE.
(1)若∠A0E=50°,求∠ACB的度数;
(2)求证:AE=CF.
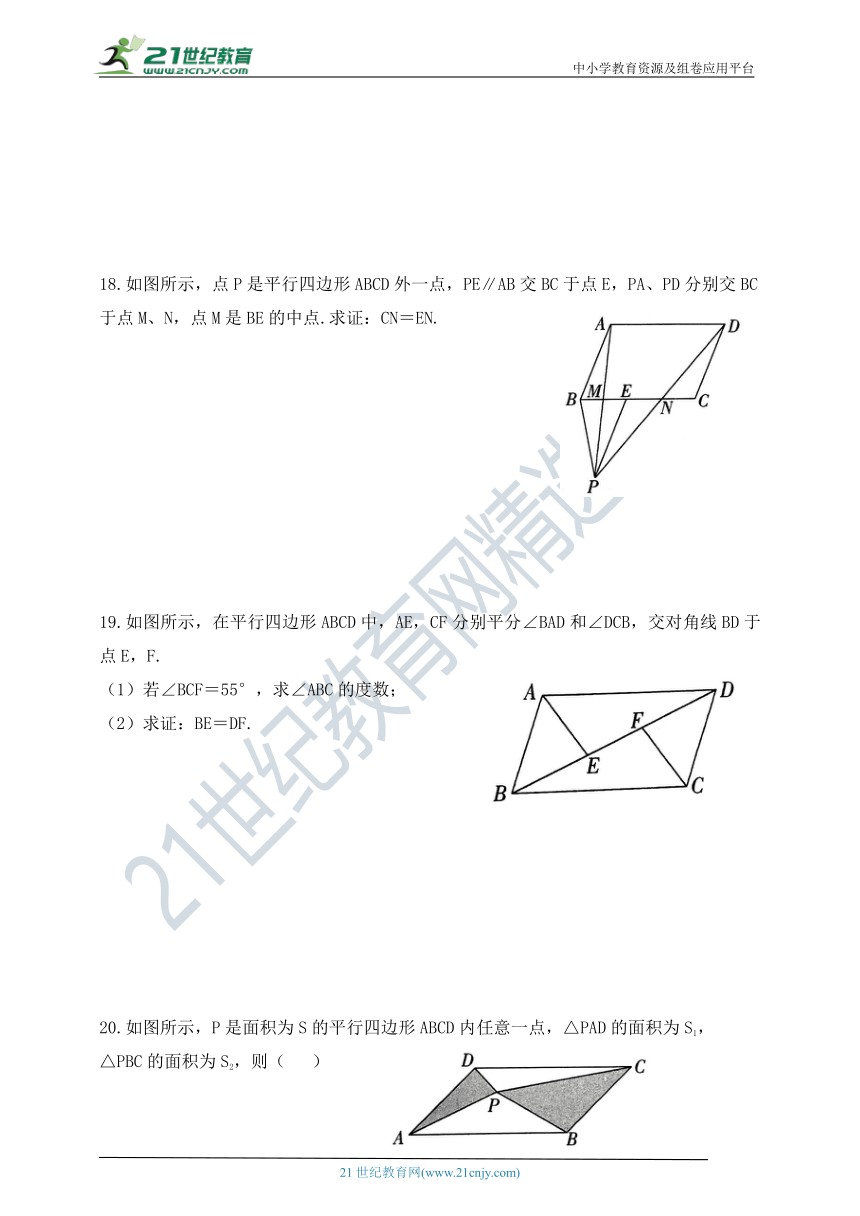
18.如图所示,点P是平行四边形ABCD外一点,PE∥AB交BC于点E,PA、PD分别交BC于点M、N,点M是BE的中点.求证:CN=EN.
19.如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BE=DF.
20.如图所示,P是面积为S的平行四边形ABCD内任意一点,△PAD的面积为S1,
△PBC的面积为S2,则( )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
21.如图所示,平行四边形ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE
与DF交于点H,则∠BHF=_________度.
22.如图所示,平行四边形ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为__________.
23.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F.求证:AE=CF.
24.如图所示,已知平行四边形ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
(1)求△ADO的周长;
(2)求证:△AD0是直角三角形.
25.如图所示,长方形ABCD的面积为Scm2,对角线交于点O.以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AOC2B,……,以此类推,平行四边形AOnCn+1B的面积为( )
A. B. C. D.
26.如图①,在平行四边形ABCD中,对角线AC,BD相交于点O,过O点作直线EF,分别交BC、AD于点E、F.
(1)证明:OF=OE;
(2)小明从图①中找到了一种将平行四边形的面积平分的方法.图②是一块纸片,其
形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将其分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
参考答案
1.C 2.B 3.B 4.A 5.B 6.D 7.D
8.证明 ∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴BE=DF.
9.解析 (1)∵四边形ABCD是平行四边形,
∴0A=0C=AC=5,0B=0D=BD=13,
∵AC⊥BC,∴BC==12.
(2)平行四边形ABCD的面积=BC·AC=12×10=120.
10.C
11.解析 如图,连接BD,过点C作CE∥BD,交AB的延长线于点E,连接DE,则S△AED=S四边形ABCD.
理由:CE∥BD,∴CE与DB间的距离都相等,S△BDC和S△BDE的底边相等且CE与DB间的距离相等,即两个三角形同底上的高相等,∴S△BDC=S△BDE,∵S△AED=S△ADB+S△BDE,S四边形ABCD=S△ABD+S△BDC,∴S△AED=S四边形ABCD .
12.D 13.B 14.B 15. 26°
16.证明 ∵四边形ABCD是平行四边形,∴AB=CD, BC=AD, ∠B=∠D,
∵E、F分别是AB,CD的中点,∴BE=,DF=,∴BE=DF,
在ABEC与ADFA中,,∴△BEC≌△DFA(SAS).
17.解析 (1)∵AE⊥BD,∴∠AEO=90°,
∵∠AOE=50°,∴∠EA0=40°,
∵AC平分∠DAE,∴∠DAC=∠EA0=40°,
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ACB=∠DAC=40°.
(2)证明: ∵四边形ABCD是平行四边形,∴0A=0C,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴AE=CF.
18.证明 ∵PE//AB, M是BE的中点,∴∠BAM=∠EPM,BM=ME,
又∵∠AMB=∠PME,∴△ABM≌△PEM( AAS),∴PE=AB,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴PE=CD,
又∵PE∥AB, AB∥CD,∴PE∥CD,∴∠NDC=∠NPE,
又∵∠DNC=∠PNE,PE=CD,∴△DCN≌△PEN( AAS),∴CN=EN.
19.解析 (1)∵四边形ABCD是平行四边形,∴AB//CD,∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,∴∠BCD=2∠BCF,
∵∠BCF=55°,∴∠BCD=110°,∴∠ABC=180°-110°=70°.
(2)证明: ∵四边形ABCD是平行四边形,∴AB∥CD, AB=CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD,∠DCF=∠DCB.∴∠BAE=∠DCF,
又∵AB=CD,∠ABE=∠CDF,∴△ABE≌△CDF(ASA),∴BE=DF.
20.C 21. 61 22.
23.证明 ∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,∴∠EAC=∠FCO,
在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴AE=CF.
24.解析 (1)∵四边形ABCD是平行四边形,∴对角线AC与BD互相平分,
∴0A=0C=AC,OB=0D=BD,
∵AC=26,BD=10,∴0A=13,0D=5,
∵AD=12,∴△AD0的周长=5+12+13=30.
(2)证明:∵0A=13,0D=5,AD=12,
∴AD2+D02=AO2,∴△AOD是直角三角形.
25.C
26.解析
(1)证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,
∴∠FAO=∠ECO.
在△AOF和△COE中,,∴△AOF≌△COE(ASA),∴OF=OE.
(2)如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
1 平行四边形的性质
知识能力全练
知识点一 平行四边形的定义
1.如图所示,AC∥HD∥GE,AG∥BF∥CE,则图中的平行四边形一共有( )
A.7个 B.8个 C.9个 D.10个
知识点二 平行四边形的性质
2.如图所示,在平行四边形ABCD中,若AB=3,BC=4,∠A=120°,则平行四边形ABCD的周长和∠1的度数分别为( )
A.7,120° B.14,60° C.12,60° D.7,60°
3.如图所示,在平行四边形ABCD中,过点C的直线CE⊥AB,交BA的延长线于点E,若∠BAD=127°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
4.平行四边形ABCD中,对角线AC和BD相交于点O,若AC=3,AB=6,BD=m,那么m的取值范围是( )
A.9<m<15 B.2<m<14 C.6<m<8 D.4<m<20
5.如图所示,在平行四边形ABCD中,点E在BC上,且CD=CE,连接DE,过点A作AF⊥DE,垂足为F,若∠DAF=48°,则∠C的度数为( )
A.84° B.96° C.98° D.106°
6.在平行四边形ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,若EF=2,则AB的长为( )
A.3 B.5 C.2或3 D.3或5
7.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
A. B.2 C. D.
8.如图所示,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
9.如图所示,平行四边形ABCD的对角线AC、BD交于点0,AC⊥BC,AC=10,BD=26.
(1)求BC的长;
(2)求平行四边形ABCD的面积.
知识点三 两条平行线间的距离
10.已知平行四边形两邻边长分别为16,20,若两条长边之间的距离为8,则两条短边之间的距离为( )
A.4 B.5 C.10 D.8
11.如图所示,已知四边形ABCD的面积为S,请画出一个与四边形ABCD面积相等的三角形,并说明理由.
巩固提高全练
12.平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.4:3:3:4 B.7:5:5:7 C.4:3:2:1 D.7:5:7:5
13.如图所示,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B=( )
A.124° B.114° C.104° D.66°
14.如图①,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一个对称图形戊,如图②所示,则图形戊中的四边形两对角线长度和为( )
A.29 B.26 C.24 D.25
15.如图所示,AC是平行四边形ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是_________.
16.如图所示,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
求证:△BEC≌△DFA.
17.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F,AC平分∠DAE.
(1)若∠A0E=50°,求∠ACB的度数;
(2)求证:AE=CF.
18.如图所示,点P是平行四边形ABCD外一点,PE∥AB交BC于点E,PA、PD分别交BC于点M、N,点M是BE的中点.求证:CN=EN.
19.如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BE=DF.
20.如图所示,P是面积为S的平行四边形ABCD内任意一点,△PAD的面积为S1,
△PBC的面积为S2,则( )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
21.如图所示,平行四边形ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE
与DF交于点H,则∠BHF=_________度.
22.如图所示,平行四边形ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为__________.
23.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F.求证:AE=CF.
24.如图所示,已知平行四边形ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
(1)求△ADO的周长;
(2)求证:△AD0是直角三角形.
25.如图所示,长方形ABCD的面积为Scm2,对角线交于点O.以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AOC2B,……,以此类推,平行四边形AOnCn+1B的面积为( )
A. B. C. D.
26.如图①,在平行四边形ABCD中,对角线AC,BD相交于点O,过O点作直线EF,分别交BC、AD于点E、F.
(1)证明:OF=OE;
(2)小明从图①中找到了一种将平行四边形的面积平分的方法.图②是一块纸片,其
形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将其分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
参考答案
1.C 2.B 3.B 4.A 5.B 6.D 7.D
8.证明 ∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴BE=DF.
9.解析 (1)∵四边形ABCD是平行四边形,
∴0A=0C=AC=5,0B=0D=BD=13,
∵AC⊥BC,∴BC==12.
(2)平行四边形ABCD的面积=BC·AC=12×10=120.
10.C
11.解析 如图,连接BD,过点C作CE∥BD,交AB的延长线于点E,连接DE,则S△AED=S四边形ABCD.
理由:CE∥BD,∴CE与DB间的距离都相等,S△BDC和S△BDE的底边相等且CE与DB间的距离相等,即两个三角形同底上的高相等,∴S△BDC=S△BDE,∵S△AED=S△ADB+S△BDE,S四边形ABCD=S△ABD+S△BDC,∴S△AED=S四边形ABCD .
12.D 13.B 14.B 15. 26°
16.证明 ∵四边形ABCD是平行四边形,∴AB=CD, BC=AD, ∠B=∠D,
∵E、F分别是AB,CD的中点,∴BE=,DF=,∴BE=DF,
在ABEC与ADFA中,,∴△BEC≌△DFA(SAS).
17.解析 (1)∵AE⊥BD,∴∠AEO=90°,
∵∠AOE=50°,∴∠EA0=40°,
∵AC平分∠DAE,∴∠DAC=∠EA0=40°,
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ACB=∠DAC=40°.
(2)证明: ∵四边形ABCD是平行四边形,∴0A=0C,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴AE=CF.
18.证明 ∵PE//AB, M是BE的中点,∴∠BAM=∠EPM,BM=ME,
又∵∠AMB=∠PME,∴△ABM≌△PEM( AAS),∴PE=AB,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴PE=CD,
又∵PE∥AB, AB∥CD,∴PE∥CD,∴∠NDC=∠NPE,
又∵∠DNC=∠PNE,PE=CD,∴△DCN≌△PEN( AAS),∴CN=EN.
19.解析 (1)∵四边形ABCD是平行四边形,∴AB//CD,∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,∴∠BCD=2∠BCF,
∵∠BCF=55°,∴∠BCD=110°,∴∠ABC=180°-110°=70°.
(2)证明: ∵四边形ABCD是平行四边形,∴AB∥CD, AB=CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD,∠DCF=∠DCB.∴∠BAE=∠DCF,
又∵AB=CD,∠ABE=∠CDF,∴△ABE≌△CDF(ASA),∴BE=DF.
20.C 21. 61 22.
23.证明 ∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,∴∠EAC=∠FCO,
在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴AE=CF.
24.解析 (1)∵四边形ABCD是平行四边形,∴对角线AC与BD互相平分,
∴0A=0C=AC,OB=0D=BD,
∵AC=26,BD=10,∴0A=13,0D=5,
∵AD=12,∴△AD0的周长=5+12+13=30.
(2)证明:∵0A=13,0D=5,AD=12,
∴AD2+D02=AO2,∴△AOD是直角三角形.
25.C
26.解析
(1)证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,
∴∠FAO=∠ECO.
在△AOF和△COE中,,∴△AOF≌△COE(ASA),∴OF=OE.
(2)如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
