2021-2022学年 人教版八年级数学上册12.2.3 用“角边角”判定三角形全等(共28张)
文档属性
| 名称 | 2021-2022学年 人教版八年级数学上册12.2.3 用“角边角”判定三角形全等(共28张) |  | |
| 格式 | zip | ||
| 文件大小 | 335.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 20:47:34 | ||
图片预览






文档简介
(共28张PPT)
人教版 数学 八年级上册
第2节 全等三角形的判定
第3课时 用“角边角”判定三角形全等
第十二章 全等三角形
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2.三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C' (SSS).
B
C
A
B'
C'
A'
复习旧知
3.两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
B
C
A
B'
C'
A'
1.理解并掌握三角形全等判定“角边角”条件的内容.
2.熟练利用“角边角”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
作法: (1)画A′B′=AB.
(2)在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,
A′D,B′E相交于点C′.
(3)△A′B′C′即为所作三角形.
导入新知
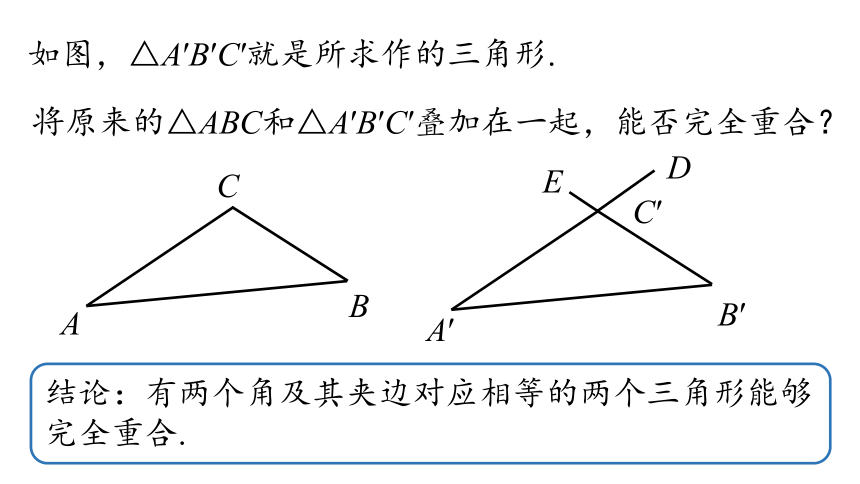
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
新知 三角形全等的基本事实:角边角(ASA)
B
C
A
B'
C'
A'
合作探究
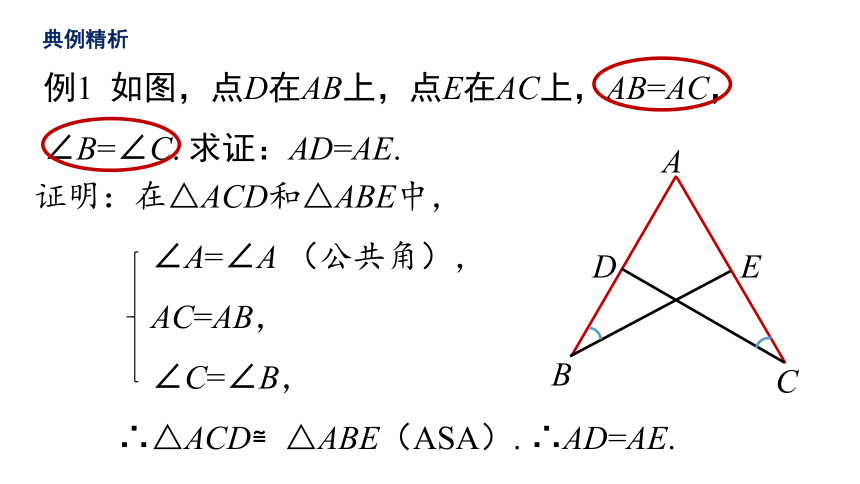
例1 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA). ∴AD=AE.
D
E
B
C
A
典例精析
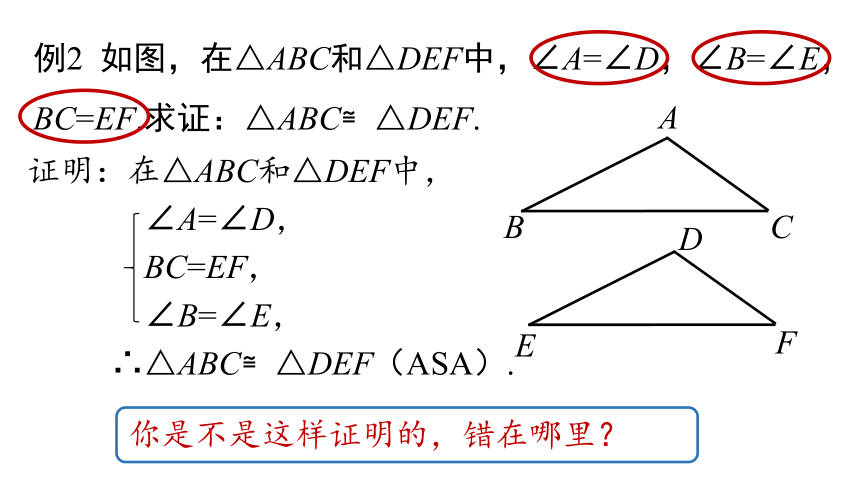
例2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
你是不是这样证明的,错在哪里?
证明:∵在△ABC和△DEF中,∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
例2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
例3 如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.求证:AB=AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,
∠1 =∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
三角形内角和都是180°
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA),
∴AB=AD.
A
B
C
D
1
2
例3 如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.求证:AB=AD.
例4 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,即DE的长就是AB的长.
A
B
C
D
F
E
┐
┐
例4 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
三角形全等的判定
分类
探讨
ASA
应用
两角及其夹边分别相等;
两角及其中一角的对边分别相等
两角和它们的夹边分别相等的两个三角形全等
利用“ASA”解决实际问题
归纳新知
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( )
A.甲 B.乙
C.甲和乙都是 D.都不是
B
课后练习
2.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( )
A.∠A=∠D
B.AB=DE
C.∠A=∠E
D.∠B=∠E
A
3.【2020·铜仁】如图,∠B=∠E,BF=EC,AC∥DF.求证△ABC≌△DEF.
4.【2019·临沂】如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
B
5.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A.10 B.6 C.5 D.4.5
C
6.【2020·南充】如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证AB=CD.
7.【2020·黄石】如图,AB=AE,AB∥DE,∠DAB=70°,∠E=40°.
(1)求∠DAE的度数;
解:∵AB∥DE,∠E=40°,
∴∠EAB=∠E=40°.
∵∠DAB=70°,
∴∠DAE=∠DAB-∠EAB=70°-40°=30°.
(2)若∠B=30°,求证AD=BC.
8.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若AB=BC+AD,判断BE与AF的位置关系,并说明理由.
解:BE⊥AF.理由如下:
由(1)知△ADE≌△FCE,
∴AE=FE,AD=CF.
∵AB=BC+AD,∴AB=BC+CF,即AB=FB.
再 见
人教版 数学 八年级上册
第2节 全等三角形的判定
第3课时 用“角边角”判定三角形全等
第十二章 全等三角形
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2.三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C' (SSS).
B
C
A
B'
C'
A'
复习旧知
3.两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
B
C
A
B'
C'
A'
1.理解并掌握三角形全等判定“角边角”条件的内容.
2.熟练利用“角边角”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
作法: (1)画A′B′=AB.
(2)在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,
A′D,B′E相交于点C′.
(3)△A′B′C′即为所作三角形.
导入新知
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
新知 三角形全等的基本事实:角边角(ASA)
B
C
A
B'
C'
A'
合作探究
例1 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA). ∴AD=AE.
D
E
B
C
A
典例精析
例2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
你是不是这样证明的,错在哪里?
证明:∵在△ABC和△DEF中,∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
例2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
例3 如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.求证:AB=AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,
∠1 =∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
三角形内角和都是180°
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA),
∴AB=AD.
A
B
C
D
1
2
例3 如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.求证:AB=AD.
例4 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,即DE的长就是AB的长.
A
B
C
D
F
E
┐
┐
例4 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
三角形全等的判定
分类
探讨
ASA
应用
两角及其夹边分别相等;
两角及其中一角的对边分别相等
两角和它们的夹边分别相等的两个三角形全等
利用“ASA”解决实际问题
归纳新知
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( )
A.甲 B.乙
C.甲和乙都是 D.都不是
B
课后练习
2.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( )
A.∠A=∠D
B.AB=DE
C.∠A=∠E
D.∠B=∠E
A
3.【2020·铜仁】如图,∠B=∠E,BF=EC,AC∥DF.求证△ABC≌△DEF.
4.【2019·临沂】如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
B
5.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A.10 B.6 C.5 D.4.5
C
6.【2020·南充】如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证AB=CD.
7.【2020·黄石】如图,AB=AE,AB∥DE,∠DAB=70°,∠E=40°.
(1)求∠DAE的度数;
解:∵AB∥DE,∠E=40°,
∴∠EAB=∠E=40°.
∵∠DAB=70°,
∴∠DAE=∠DAB-∠EAB=70°-40°=30°.
(2)若∠B=30°,求证AD=BC.
8.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若AB=BC+AD,判断BE与AF的位置关系,并说明理由.
解:BE⊥AF.理由如下:
由(1)知△ADE≌△FCE,
∴AE=FE,AD=CF.
∵AB=BC+AD,∴AB=BC+CF,即AB=FB.
再 见
