2018-2019学年安徽省蚌埠十二中九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2018-2019学年安徽省蚌埠十二中九年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 737.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 07:43:43 | ||
图片预览




文档简介
2018-2019学年安徽省蚌埠十二中九年级第一学期期中数学试卷
一、选择题(每小题4分,共40分)
1.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+x﹣2 C.y=2x+1 D.y2=x2+3x
2.反比例函数y=的图象位于( )
A.第一、三象限 B.第二、三象限
C.第一、二象限 D.第二、四象限
3.若=,则下列各式中不正确的是( )
A.= B.= C.=4 D.=
4.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=的图象上三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1<0<y2<y3 B.y1>0>y2>y3 C.y1<0<y3<y2 D.y1>0>y3>y2
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为( )
A.0 B.﹣1 C.1 D.2
6.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
A.y=3(x+3)2﹣2 B.y=3(x+3)2+2
C.y=3(x﹣3)2﹣2 D.y=3(x﹣3)2+2
7.若===k,则k的值为( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
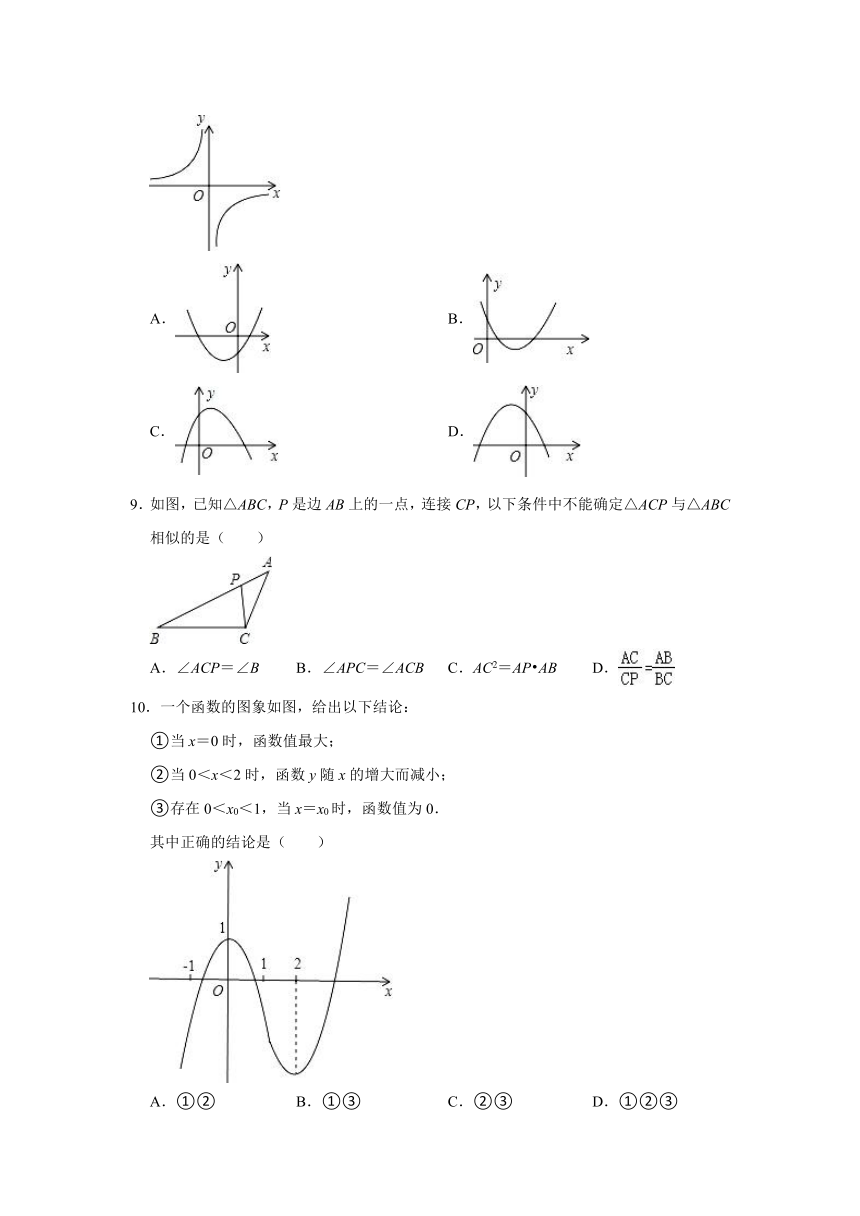
8.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A. B.
C. D.
9.如图,已知△ABC,P是边AB上的一点,连接CP,以下条件中不能确定△ACP与△ABC相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.
10.一个函数的图象如图,给出以下结论:
①当x=0时,函数值最大;
②当0<x<2时,函数y随x的增大而减小;
③存在0<x0<1,当x=x0时,函数值为0.
其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(共4小题,每小题5分,满分20分)
11.已知反比例函数y=的图象经过点(1,2),则k的值是 .
12.如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,则支撑点C到端点A的距离约为 (≈2.2).
13.如图,在△ABC中,D是AB边上一点,连接CD,若AD=4,AC=6,要使△ADC与△ACB相似,则BD= .
14.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 .
三、解答题(共90分)
15.用配方法求二次函数y=x2+2x﹣4图象的对称轴、顶点坐标.
16.已知如图,点D、E、F为△ABC中各边上一点,EF∥BC,交AD于点H,求证:=.
17.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
18.气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)是气体体积V(单位:立方米)的反比例函数,其图象如图所示.
(1)写出p关于V的函数解析式;
(2)当气球内气体的气压大于144千帕时,气球就会爆炸.为了安全起见,气体的体积应不小于多少立方米?(保留两个有效数字)
19.在Rt△ABC中,∠B=90°,若AB=BE=EF=FC=2.求证:△AEF∽△CEA.
20.已知某二次函数图象的顶点坐标为(3,﹣2)且与y轴交于(0,).
(1)求这个二次函数的解析式.
(2)若这抛物线经过点(2,y1),(﹣1,y2),(,y3),请你先画出草图,再根据草图试比较y1,y2,y3的大小.
21.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.求证:△APE∽△FPA.
22.在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
23.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(2)政府补贴x为多少时,种植这种绿色蔬菜的总收益最大(不用求出最大值)?
参考答案
一、选择题(每小题4分,共40分)
1.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+x﹣2 C.y=2x+1 D.y2=x2+3x
【分析】二次函数的一般形式为:y=ax2+bx+c(a≠0).
解:根据二次函数的一般形式可知:y=x2+x﹣2是二次函数.
故选:B.
2.反比例函数y=的图象位于( )
A.第一、三象限 B.第二、三象限
C.第一、二象限 D.第二、四象限
【分析】由反比例函数k>0,函数经过一三象限即可求解;
解:∵k=2>0,
∴反比例函数经过第一、三象限;
故选:A.
3.若=,则下列各式中不正确的是( )
A.= B.= C.=4 D.=
【分析】根据x和y的比例关系设出x和y的值,依次判断每个选项即可得出答案.
解:∵,
∴设x=3k,则y=4k,
∴,,,,
∴B选项计算不正确,
故选:B.
4.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=的图象上三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1<0<y2<y3 B.y1>0>y2>y3 C.y1<0<y3<y2 D.y1>0>y3>y2
【分析】根据反比例函数的增减性解答即可.
解:∵k=﹣4<0,故反比例函数图象的两个分支在第二四象限,且在每个象限内y随x的增大而增大,
又∵(x2,y2),(x3,y3)是双曲线y=上的两点,且0<x2<x3,∴0>y3>y2,
又∵x1<0,故(x1,y1)在第二象限,y1>0,
∴y1>0>y3>y2.
故选:D.
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为( )
A.0 B.﹣1 C.1 D.2
【分析】由“对称轴是直线x=1,且经过点P(3,0)”可知抛物线与x轴的另一个交点是(﹣1,0),代入抛物线方程即可解得.
解:因为对称轴是直线x=1且经过点P(3,0)
所以抛物线与x轴的另一个交点是(﹣1,0)
代入抛物线解析式y=ax2+bx+c中,得a﹣b+c=0.
故选:A.
6.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
A.y=3(x+3)2﹣2 B.y=3(x+3)2+2
C.y=3(x﹣3)2﹣2 D.y=3(x﹣3)2+2
【分析】根据二次函数图象左加右减,上加下减的平移规律进行求解.
解:抛物线y=3x2先向上平移2个单位,得:y=3x2+2;
再向右平移3个单位,得:y=3(x﹣3)2+2;
故选:D.
7.若===k,则k的值为( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
【分析】分①a+b+c=0时,用c表示出a+b,然后求解,②a+b+c≠0时,利用等比性质列式计算即可得解.
解:①a+b+c=0时,a+b=﹣c,
所以,k===﹣1;
②a+b+c≠0时,=====2,
所以,k=2,
综上所述,k的值为2或﹣1.
故选:C.
8.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A. B.
C. D.
【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
解:∵函数y=的图象经过二、四象限,∴k<0,
∴抛物线开口向下,对称轴x=﹣=<0,
即对称轴在y轴的左边.
故选:D.
9.如图,已知△ABC,P是边AB上的一点,连接CP,以下条件中不能确定△ACP与△ABC相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.
【分析】当△ACP∽△ABC时,可得对应边成比例,对应角相等,依此判断.
解:当△ACP∽△ABC,有:∠ACP=∠B,∠APC=∠ACB,,
即AC2=AP AB.
故A、B、C、都能确定△ACP∽△ABC,D不能确定.
故选:D.
10.一个函数的图象如图,给出以下结论:
①当x=0时,函数值最大;
②当0<x<2时,函数y随x的增大而减小;
③存在0<x0<1,当x=x0时,函数值为0.
其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
【分析】看图,可知当X为0时函数不是最大值;当0<x<2时,函数的y随x的增大而减小,故②正确;如图可知在0<x0<1,当x=x0时,函数值为0.
解:函数值大,就是对应的点高,因而①当x=0时,函数值最大;不正确.
②当0<x<2时,函数对应的点函数对应的点越向右越向下,即y随x的增大而减小.
函数在大于0并且小于1这部分,存在值是0的点,即图象与x轴有交点,③存在0<x0<1,当x=x0时,函数值为0,正确.
故选:C.
二、填空题(共4小题,每小题5分,满分20分)
11.已知反比例函数y=的图象经过点(1,2),则k的值是 2 .
【分析】把(1,2)代入函数y=,可求出k的值.
解:∵点(1,2)在函数y=上,则有2=,即k=2.
故答案为:2.
12.如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,则支撑点C到端点A的距离约为 48 (≈2.2).
【分析】由黄金分割点的定义求解即可.
解:∵点C是靠近点B的黄金分割点,AB=80cm,
∴AC=×80≈48(cm),
故答案为:48.
13.如图,在△ABC中,D是AB边上一点,连接CD,若AD=4,AC=6,要使△ADC与△ACB相似,则BD= 5 .
【分析】根据相似三角形的判定定理得到△ADC∽△ACB的条件是=,于是得到AC2=AB AD,代入数据即可得到答案.
解:∵∠A=∠A,
∴要使△ADC∽△ACB,必有=,
∴AC2=AB AD,
∵AD=4,AC=6,
∴62=4AB,
∴AB=9,
∴BD=AB﹣AD=9﹣4=5,
即要使△ADC与△ACB相似,则BD=5,
故答案为:5.
14.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 ﹣1.5或 .
【分析】分类讨论抛物线对称轴的位置确定出m的范围即可.
解:由二次函数y=x2﹣2mx(m为常数),得到对称轴为直线x=m,抛物线开口向上,
当m>2时,由题意得:当x=2时,y最小值为﹣2,代入得:4﹣4m=﹣2,即m=1.5<2,不合题意,舍去;
当﹣1≤m≤2时,由题意得:当x=m时,y最小值为﹣2,代入得:﹣m2=﹣2,即m=或m=﹣(舍去);
当m<﹣1时,由题意得:当x=﹣1时,y最小值为﹣2,代入得:1+2m=﹣2,即m=﹣1.5,
综上,m的值是﹣1.5或,
故答案为:﹣1.5或.
三、解答题(共90分)
15.用配方法求二次函数y=x2+2x﹣4图象的对称轴、顶点坐标.
【分析】先配方,得到二次函数的顶点坐标式,即可直接写出其对称轴和顶点坐标;
解:配方得:y=(x+1)2﹣5;
∴该函数图象的对称轴为直线x=﹣1、顶点坐标(﹣1,﹣5).
16.已知如图,点D、E、F为△ABC中各边上一点,EF∥BC,交AD于点H,求证:=.
【分析】由EF∥BC可得△AEH∽△ABD,∴EH:BD=AH:AD;同理可得HF:CD=AH:AD,从而得结论.
【解答】证明:∵EF∥BC,
∴△AEH∽△ABD,
∴EH:BD=AH:AD,
同理可得HF:CD=AH:AD,
∴EH:BD=HF:CD,
即=.
17.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
【分析】运用设k法,再进一步得到关于k的方程,解得k的值后,即可求得a、b、c的值.
解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
18.气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)是气体体积V(单位:立方米)的反比例函数,其图象如图所示.
(1)写出p关于V的函数解析式;
(2)当气球内气体的气压大于144千帕时,气球就会爆炸.为了安全起见,气体的体积应不小于多少立方米?(保留两个有效数字)
【分析】(1)根据:气体温度=气体的气压P×气体体积V=60×1.6=96,即PV=96,可求P关于V的函数解析式;
(2)将P=144代入(1)中的函数式中,可求气球的体积V.
解:(1)将A(1.5,64)代入,
得,
∴k=96.
∴;
(2)∵p≤144,
∴,
即V≥0.67立方米.
19.在Rt△ABC中,∠B=90°,若AB=BE=EF=FC=2.求证:△AEF∽△CEA.
【分析】根据勾股定理得到AE==2,推出AE:EF=CE:AE,然后根据相似三角形的判定定理即可得到结论.
【解答】证明:∵∠B=90°,AB=BE=EF=FC=2.
∴AE==2,
∴AE:EF=2:2=,CE:AE=4:2=,
∴AE:EF=CE:AE,
∵∠AEF=∠AEC,
∴△AEF∽△CEA.
20.已知某二次函数图象的顶点坐标为(3,﹣2)且与y轴交于(0,).
(1)求这个二次函数的解析式.
(2)若这抛物线经过点(2,y1),(﹣1,y2),(,y3),请你先画出草图,再根据草图试比较y1,y2,y3的大小.
【分析】(1)由二次函数图象的顶点坐标为(3,﹣2),设解析式为y=a(x﹣3)2﹣2,将(0,)代入即得答案;
(2)画出草图,即可得y2>y1>y3.
解:(1)∵二次函数图象的顶点坐标为(3,﹣2),
∴设所求二次函数的解析式为y=a(x﹣3)2﹣2,
∵图象过(0,),
∴=a(0﹣3)2﹣2,
解得a=,
∴所求二次函数的解析式为y=(x﹣3)2﹣2=x2﹣3x+;
(2)如图:
由图知y2>y1>y3.
21.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.求证:△APE∽△FPA.
【分析】根菱形ABCD的性质证明△APD≌△CPD(SAS),利用两组角相等证明两三角形相似即可.
【解答】证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP.
又∵PD=PD,
∴△APD≌△CPD(SAS),
∴∠DAP=∠DCP,
∵CD∥AB,
∴∠DCF=∠DAP=∠CFB,
又∵∠FPA=∠FPA,
∴△APE∽△FPA.
22.在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
【分析】(1)根据抛物线与x轴的交点A与C坐标设出抛物线的二根式方程,将B坐标代入即可确定出解析式;
(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积﹣三角形AOB面积,求出即可.
解:(1)设抛物线解析式为y=a(x+4)(x﹣2),
将B(0,﹣4)代入得:﹣4=﹣8a,即a=,
则抛物线解析式为y=(x+4)(x﹣2)=x2+x﹣4;
(2)过M作MN⊥x轴,
将x=m代入抛物线得:y=m2+m﹣4,即M(m,m2+m﹣4),
∴MN=|m2+m﹣4|=﹣m2﹣m+4,ON=﹣m,
∵A(﹣4,0),B(0,﹣4),∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB
=×(4+m)×(﹣m2﹣m+4)+×(﹣m)×(﹣m2﹣m+4+4)﹣×4×4
=2(﹣m2﹣m+4)﹣2m﹣8
=﹣m2﹣4m
=﹣(m+2)2+4,
当m=﹣2时,S取得最大值,最大值为4.
23.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(2)政府补贴x为多少时,种植这种绿色蔬菜的总收益最大(不用求出最大值)?
【分析】(1)设种植亩数y与政府补贴数额x之间的函数关系式为y=kx+b,每亩蔬菜的收益z与政府补贴数额x之间的函数关系式为z=k1x+b1,由待定系数法求出其解即可;
(2)设总收益为W元,由总收益=每亩的收益×亩数就可以得出W与x之间的关系式,由二次函数的性质就可以得出结论.
解:(1)设种植亩数y与政府补贴数额x之间的函数关系式为y=kx+b,每亩蔬菜的收益z与政府补贴数额x之间的函数关系式为z=k1x+b1,
由题意,得,,
解得,,
则y=8x+800,z=﹣3x+3000;
(2)设总收益为W元,则
W=yz=(8x+800)(﹣3x+3000)
=﹣24x2+21600x+2400000,
∴x=﹣=﹣=450时,总收益最大.
一、选择题(每小题4分,共40分)
1.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+x﹣2 C.y=2x+1 D.y2=x2+3x
2.反比例函数y=的图象位于( )
A.第一、三象限 B.第二、三象限
C.第一、二象限 D.第二、四象限
3.若=,则下列各式中不正确的是( )
A.= B.= C.=4 D.=
4.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=的图象上三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1<0<y2<y3 B.y1>0>y2>y3 C.y1<0<y3<y2 D.y1>0>y3>y2
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为( )
A.0 B.﹣1 C.1 D.2
6.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
A.y=3(x+3)2﹣2 B.y=3(x+3)2+2
C.y=3(x﹣3)2﹣2 D.y=3(x﹣3)2+2
7.若===k,则k的值为( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
8.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A. B.
C. D.
9.如图,已知△ABC,P是边AB上的一点,连接CP,以下条件中不能确定△ACP与△ABC相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.
10.一个函数的图象如图,给出以下结论:
①当x=0时,函数值最大;
②当0<x<2时,函数y随x的增大而减小;
③存在0<x0<1,当x=x0时,函数值为0.
其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(共4小题,每小题5分,满分20分)
11.已知反比例函数y=的图象经过点(1,2),则k的值是 .
12.如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,则支撑点C到端点A的距离约为 (≈2.2).
13.如图,在△ABC中,D是AB边上一点,连接CD,若AD=4,AC=6,要使△ADC与△ACB相似,则BD= .
14.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 .
三、解答题(共90分)
15.用配方法求二次函数y=x2+2x﹣4图象的对称轴、顶点坐标.
16.已知如图,点D、E、F为△ABC中各边上一点,EF∥BC,交AD于点H,求证:=.
17.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
18.气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)是气体体积V(单位:立方米)的反比例函数,其图象如图所示.
(1)写出p关于V的函数解析式;
(2)当气球内气体的气压大于144千帕时,气球就会爆炸.为了安全起见,气体的体积应不小于多少立方米?(保留两个有效数字)
19.在Rt△ABC中,∠B=90°,若AB=BE=EF=FC=2.求证:△AEF∽△CEA.
20.已知某二次函数图象的顶点坐标为(3,﹣2)且与y轴交于(0,).
(1)求这个二次函数的解析式.
(2)若这抛物线经过点(2,y1),(﹣1,y2),(,y3),请你先画出草图,再根据草图试比较y1,y2,y3的大小.
21.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.求证:△APE∽△FPA.
22.在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
23.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(2)政府补贴x为多少时,种植这种绿色蔬菜的总收益最大(不用求出最大值)?
参考答案
一、选择题(每小题4分,共40分)
1.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+x﹣2 C.y=2x+1 D.y2=x2+3x
【分析】二次函数的一般形式为:y=ax2+bx+c(a≠0).
解:根据二次函数的一般形式可知:y=x2+x﹣2是二次函数.
故选:B.
2.反比例函数y=的图象位于( )
A.第一、三象限 B.第二、三象限
C.第一、二象限 D.第二、四象限
【分析】由反比例函数k>0,函数经过一三象限即可求解;
解:∵k=2>0,
∴反比例函数经过第一、三象限;
故选:A.
3.若=,则下列各式中不正确的是( )
A.= B.= C.=4 D.=
【分析】根据x和y的比例关系设出x和y的值,依次判断每个选项即可得出答案.
解:∵,
∴设x=3k,则y=4k,
∴,,,,
∴B选项计算不正确,
故选:B.
4.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=的图象上三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1<0<y2<y3 B.y1>0>y2>y3 C.y1<0<y3<y2 D.y1>0>y3>y2
【分析】根据反比例函数的增减性解答即可.
解:∵k=﹣4<0,故反比例函数图象的两个分支在第二四象限,且在每个象限内y随x的增大而增大,
又∵(x2,y2),(x3,y3)是双曲线y=上的两点,且0<x2<x3,∴0>y3>y2,
又∵x1<0,故(x1,y1)在第二象限,y1>0,
∴y1>0>y3>y2.
故选:D.
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为( )
A.0 B.﹣1 C.1 D.2
【分析】由“对称轴是直线x=1,且经过点P(3,0)”可知抛物线与x轴的另一个交点是(﹣1,0),代入抛物线方程即可解得.
解:因为对称轴是直线x=1且经过点P(3,0)
所以抛物线与x轴的另一个交点是(﹣1,0)
代入抛物线解析式y=ax2+bx+c中,得a﹣b+c=0.
故选:A.
6.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
A.y=3(x+3)2﹣2 B.y=3(x+3)2+2
C.y=3(x﹣3)2﹣2 D.y=3(x﹣3)2+2
【分析】根据二次函数图象左加右减,上加下减的平移规律进行求解.
解:抛物线y=3x2先向上平移2个单位,得:y=3x2+2;
再向右平移3个单位,得:y=3(x﹣3)2+2;
故选:D.
7.若===k,则k的值为( )
A.2 B.﹣1 C.2或﹣1 D.﹣2或1
【分析】分①a+b+c=0时,用c表示出a+b,然后求解,②a+b+c≠0时,利用等比性质列式计算即可得解.
解:①a+b+c=0时,a+b=﹣c,
所以,k===﹣1;
②a+b+c≠0时,=====2,
所以,k=2,
综上所述,k的值为2或﹣1.
故选:C.
8.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A. B.
C. D.
【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
解:∵函数y=的图象经过二、四象限,∴k<0,
∴抛物线开口向下,对称轴x=﹣=<0,
即对称轴在y轴的左边.
故选:D.
9.如图,已知△ABC,P是边AB上的一点,连接CP,以下条件中不能确定△ACP与△ABC相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB C.AC2=AP AB D.
【分析】当△ACP∽△ABC时,可得对应边成比例,对应角相等,依此判断.
解:当△ACP∽△ABC,有:∠ACP=∠B,∠APC=∠ACB,,
即AC2=AP AB.
故A、B、C、都能确定△ACP∽△ABC,D不能确定.
故选:D.
10.一个函数的图象如图,给出以下结论:
①当x=0时,函数值最大;
②当0<x<2时,函数y随x的增大而减小;
③存在0<x0<1,当x=x0时,函数值为0.
其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
【分析】看图,可知当X为0时函数不是最大值;当0<x<2时,函数的y随x的增大而减小,故②正确;如图可知在0<x0<1,当x=x0时,函数值为0.
解:函数值大,就是对应的点高,因而①当x=0时,函数值最大;不正确.
②当0<x<2时,函数对应的点函数对应的点越向右越向下,即y随x的增大而减小.
函数在大于0并且小于1这部分,存在值是0的点,即图象与x轴有交点,③存在0<x0<1,当x=x0时,函数值为0,正确.
故选:C.
二、填空题(共4小题,每小题5分,满分20分)
11.已知反比例函数y=的图象经过点(1,2),则k的值是 2 .
【分析】把(1,2)代入函数y=,可求出k的值.
解:∵点(1,2)在函数y=上,则有2=,即k=2.
故答案为:2.
12.如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,则支撑点C到端点A的距离约为 48 (≈2.2).
【分析】由黄金分割点的定义求解即可.
解:∵点C是靠近点B的黄金分割点,AB=80cm,
∴AC=×80≈48(cm),
故答案为:48.
13.如图,在△ABC中,D是AB边上一点,连接CD,若AD=4,AC=6,要使△ADC与△ACB相似,则BD= 5 .
【分析】根据相似三角形的判定定理得到△ADC∽△ACB的条件是=,于是得到AC2=AB AD,代入数据即可得到答案.
解:∵∠A=∠A,
∴要使△ADC∽△ACB,必有=,
∴AC2=AB AD,
∵AD=4,AC=6,
∴62=4AB,
∴AB=9,
∴BD=AB﹣AD=9﹣4=5,
即要使△ADC与△ACB相似,则BD=5,
故答案为:5.
14.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 ﹣1.5或 .
【分析】分类讨论抛物线对称轴的位置确定出m的范围即可.
解:由二次函数y=x2﹣2mx(m为常数),得到对称轴为直线x=m,抛物线开口向上,
当m>2时,由题意得:当x=2时,y最小值为﹣2,代入得:4﹣4m=﹣2,即m=1.5<2,不合题意,舍去;
当﹣1≤m≤2时,由题意得:当x=m时,y最小值为﹣2,代入得:﹣m2=﹣2,即m=或m=﹣(舍去);
当m<﹣1时,由题意得:当x=﹣1时,y最小值为﹣2,代入得:1+2m=﹣2,即m=﹣1.5,
综上,m的值是﹣1.5或,
故答案为:﹣1.5或.
三、解答题(共90分)
15.用配方法求二次函数y=x2+2x﹣4图象的对称轴、顶点坐标.
【分析】先配方,得到二次函数的顶点坐标式,即可直接写出其对称轴和顶点坐标;
解:配方得:y=(x+1)2﹣5;
∴该函数图象的对称轴为直线x=﹣1、顶点坐标(﹣1,﹣5).
16.已知如图,点D、E、F为△ABC中各边上一点,EF∥BC,交AD于点H,求证:=.
【分析】由EF∥BC可得△AEH∽△ABD,∴EH:BD=AH:AD;同理可得HF:CD=AH:AD,从而得结论.
【解答】证明:∵EF∥BC,
∴△AEH∽△ABD,
∴EH:BD=AH:AD,
同理可得HF:CD=AH:AD,
∴EH:BD=HF:CD,
即=.
17.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
【分析】运用设k法,再进一步得到关于k的方程,解得k的值后,即可求得a、b、c的值.
解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
18.气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)是气体体积V(单位:立方米)的反比例函数,其图象如图所示.
(1)写出p关于V的函数解析式;
(2)当气球内气体的气压大于144千帕时,气球就会爆炸.为了安全起见,气体的体积应不小于多少立方米?(保留两个有效数字)
【分析】(1)根据:气体温度=气体的气压P×气体体积V=60×1.6=96,即PV=96,可求P关于V的函数解析式;
(2)将P=144代入(1)中的函数式中,可求气球的体积V.
解:(1)将A(1.5,64)代入,
得,
∴k=96.
∴;
(2)∵p≤144,
∴,
即V≥0.67立方米.
19.在Rt△ABC中,∠B=90°,若AB=BE=EF=FC=2.求证:△AEF∽△CEA.
【分析】根据勾股定理得到AE==2,推出AE:EF=CE:AE,然后根据相似三角形的判定定理即可得到结论.
【解答】证明:∵∠B=90°,AB=BE=EF=FC=2.
∴AE==2,
∴AE:EF=2:2=,CE:AE=4:2=,
∴AE:EF=CE:AE,
∵∠AEF=∠AEC,
∴△AEF∽△CEA.
20.已知某二次函数图象的顶点坐标为(3,﹣2)且与y轴交于(0,).
(1)求这个二次函数的解析式.
(2)若这抛物线经过点(2,y1),(﹣1,y2),(,y3),请你先画出草图,再根据草图试比较y1,y2,y3的大小.
【分析】(1)由二次函数图象的顶点坐标为(3,﹣2),设解析式为y=a(x﹣3)2﹣2,将(0,)代入即得答案;
(2)画出草图,即可得y2>y1>y3.
解:(1)∵二次函数图象的顶点坐标为(3,﹣2),
∴设所求二次函数的解析式为y=a(x﹣3)2﹣2,
∵图象过(0,),
∴=a(0﹣3)2﹣2,
解得a=,
∴所求二次函数的解析式为y=(x﹣3)2﹣2=x2﹣3x+;
(2)如图:
由图知y2>y1>y3.
21.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.求证:△APE∽△FPA.
【分析】根菱形ABCD的性质证明△APD≌△CPD(SAS),利用两组角相等证明两三角形相似即可.
【解答】证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP.
又∵PD=PD,
∴△APD≌△CPD(SAS),
∴∠DAP=∠DCP,
∵CD∥AB,
∴∠DCF=∠DAP=∠CFB,
又∵∠FPA=∠FPA,
∴△APE∽△FPA.
22.在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
【分析】(1)根据抛物线与x轴的交点A与C坐标设出抛物线的二根式方程,将B坐标代入即可确定出解析式;
(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积﹣三角形AOB面积,求出即可.
解:(1)设抛物线解析式为y=a(x+4)(x﹣2),
将B(0,﹣4)代入得:﹣4=﹣8a,即a=,
则抛物线解析式为y=(x+4)(x﹣2)=x2+x﹣4;
(2)过M作MN⊥x轴,
将x=m代入抛物线得:y=m2+m﹣4,即M(m,m2+m﹣4),
∴MN=|m2+m﹣4|=﹣m2﹣m+4,ON=﹣m,
∵A(﹣4,0),B(0,﹣4),∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB
=×(4+m)×(﹣m2﹣m+4)+×(﹣m)×(﹣m2﹣m+4+4)﹣×4×4
=2(﹣m2﹣m+4)﹣2m﹣8
=﹣m2﹣4m
=﹣(m+2)2+4,
当m=﹣2时,S取得最大值,最大值为4.
23.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(2)政府补贴x为多少时,种植这种绿色蔬菜的总收益最大(不用求出最大值)?
【分析】(1)设种植亩数y与政府补贴数额x之间的函数关系式为y=kx+b,每亩蔬菜的收益z与政府补贴数额x之间的函数关系式为z=k1x+b1,由待定系数法求出其解即可;
(2)设总收益为W元,由总收益=每亩的收益×亩数就可以得出W与x之间的关系式,由二次函数的性质就可以得出结论.
解:(1)设种植亩数y与政府补贴数额x之间的函数关系式为y=kx+b,每亩蔬菜的收益z与政府补贴数额x之间的函数关系式为z=k1x+b1,
由题意,得,,
解得,,
则y=8x+800,z=﹣3x+3000;
(2)设总收益为W元,则
W=yz=(8x+800)(﹣3x+3000)
=﹣24x2+21600x+2400000,
∴x=﹣=﹣=450时,总收益最大.
同课章节目录
