4.4探索三角形相似的条件 同步练习题 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.4探索三角形相似的条件 同步练习题 2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 227.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 11:55:13 | ||
图片预览



文档简介
2021-2022北师大版九年级数学上册《4.4探索三角形相似的条件》同步练习题(附答案)
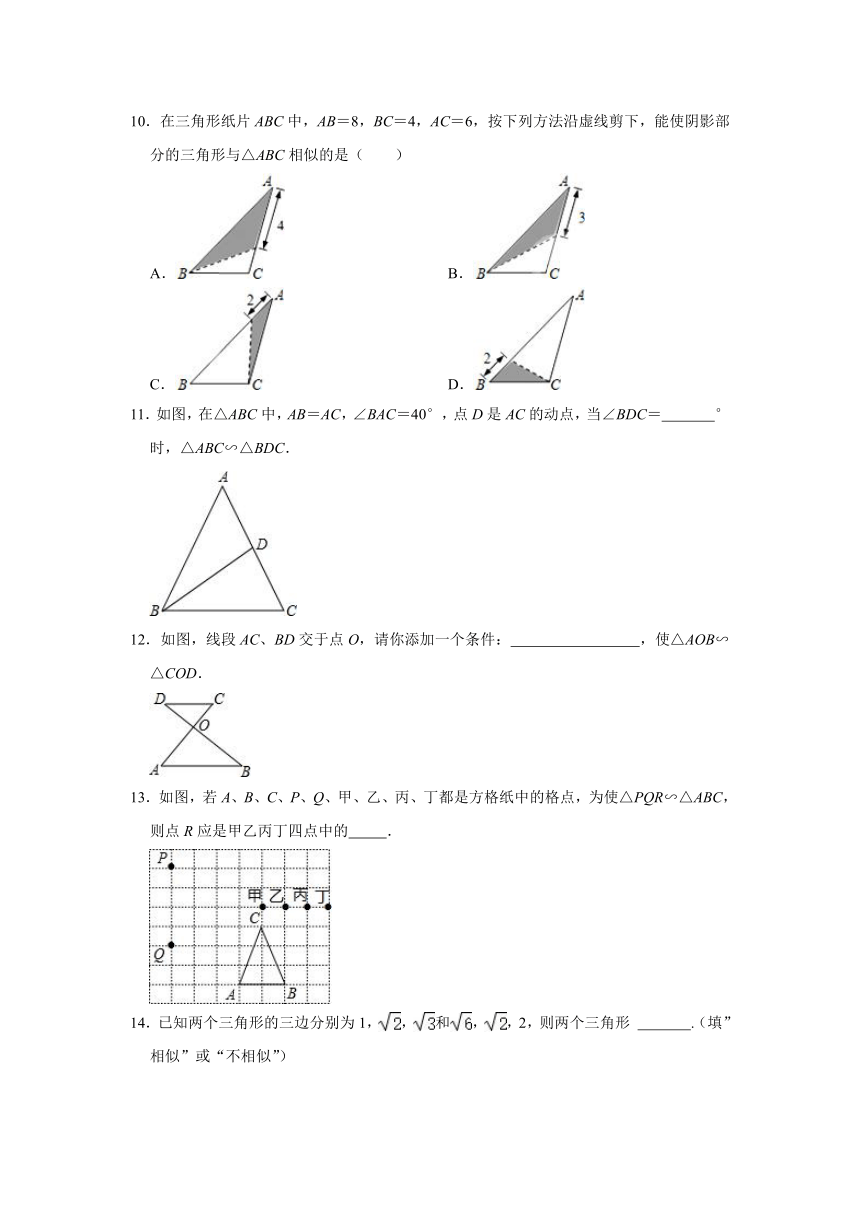
1.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
2.如图,网格中每个小正方形的边长均为1,则图中与阴影三角形相似的三角形是( )
A.A B.B C.C D.D
3.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
4.如图,△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为( )
A.4个 B.3个 C.2个 D.1个
5.如图,下列条件中,不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B.∠B=∠ACD C.∠ACD=∠BCD D.
6.下列说法错误的是( )
A.两个等边三角形一定相似 B.两个等腰三角形一定相似
C.两个等腰直角三角形一定相似 D.两个全等三角形一定相似
7.如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
8.下列各组图形中可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
9.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
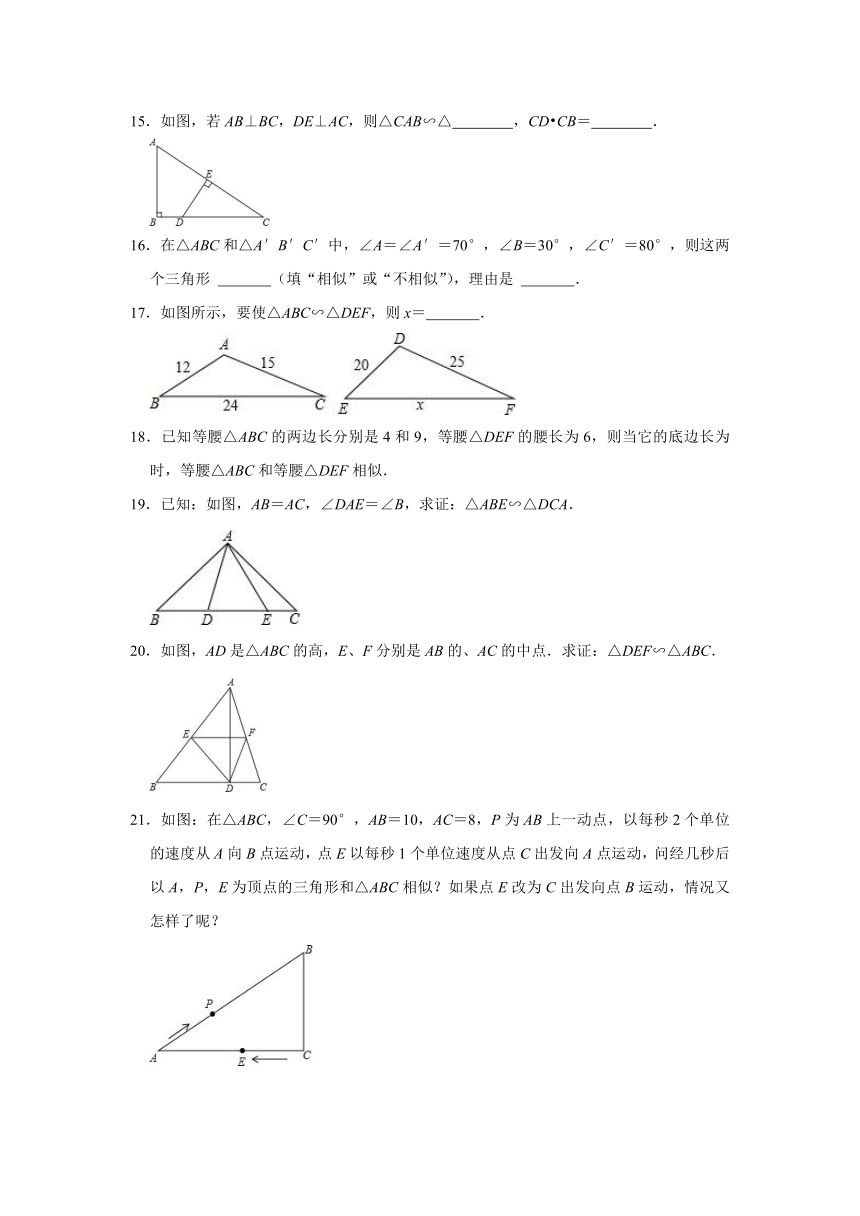
10.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
11.如图,在△ABC中,AB=AC,∠BAC=40°,点D是AC的动点,当∠BDC= °时,△ABC∽△BDC.
12.如图,线段AC、BD交于点O,请你添加一个条件: ,使△AOB∽△COD.
13.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲乙丙丁四点中的 .
14.已知两个三角形的三边分别为1,,和,,2,则两个三角形 .(填”相似”或“不相似”)
15.如图,若AB⊥BC,DE⊥AC,则△CAB∽△ ,CD CB= .
16.在△ABC和△A′B′C′中,∠A=∠A′=70°,∠B=30°,∠C′=80°,则这两个三角形 (填“相似”或“不相似”),理由是 .
17.如图所示,要使△ABC∽△DEF,则x= .
18.已知等腰△ABC的两边长分别是4和9,等腰△DEF的腰长为6,则当它的底边长为 时,等腰△ABC和等腰△DEF相似.
19.已知:如图,AB=AC,∠DAE=∠B,求证:△ABE∽△DCA.
20.如图,AD是△ABC的高,E、F分别是AB的、AC的中点.求证:△DEF∽△ABC.
21.如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
参考答案
1.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
2.解:阴影三角形两直角边长分别为2和3,
(A)该直角三角形的两直角边长分别为3和4,且≠,故不能与阴影三角形相似.
(B)该直角三角形的两直角边长分别为4和5,且,故不能与阴影三角形相似.
(C)该直角三角形的两直角边长分别为4和6,且=,故能与阴影三角形相似.
(D)该三角形的三边长分别为、、,不是直角三角形,故不能与阴影三角形相似.
故选:C.
3.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
4.解:∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC,
∵∠1=∠3,∠A=∠A,
∴△ADE∽△ACD,
∴图中与△ADE相似的三角形有2个.
故选:C.
5.解:(A)∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故A能判定△ACD∽△ABC;
(B)∵∠A=∠A,∠B=∠ACD,
∴△ACD∽△ABC,故B能判定△ACD∽△ABC;
(D)∵=,∠A=∠A,
∴△ACD∽△ABC,故D能判定△ACD∽△ABC;
故选:C.
6.解:A、两个等边三角形一定相似,所以A选项的说法正确;
B、两个等腰三角形不一定相似,如等边三角形与等腰直角三角形不相似,所以B选项的说法错误;
C、两个等腰直角三角形一定相似,所以C选项的说法正确;
D、两个全边三角形一定相似,所以D选项的说法正确.
故选:B.
7.
解:∵截得的小三角形与△ABC相似,
∴过P作AC的垂线,作AB的垂线,作BC的垂线,所截得的三角形满足题意,
则D点的位置最多有3处,
故选:B.
8.解:A、不正确,因为没有指明这个45°的角是顶角还是底角,则无法判定其相似;
B、由已知我们可以得到这是两个正三角形,从而可以根据三组对应边的比相等的两个三角形相似判定这两个三角形相似;
C、正确,已知一个角为105°,则我们可以判定其为顶角,这样我们就可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似判定这两个三角形相似;
D、正确,因为是等腰直角三角形,则我们可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定这两个三角形相似.
故选:A.
9.解:△ABC中,∠ABC=90°,AB=6,BC=3,AB:BC=2.
A、当点E的坐标为(6,0)时,∠CDE=90°,CD=2,DE=1,则AB:BC=CD:DE,△CDE∽△ABC,故本选项不符合题意;
B、当点E的坐标为(6,3)时,∠CDE=90°,CD=2,DE=2,则AB:BC≠CD:DE,△CDE与△ABC不相似,故本选项符合题意;
C、当点E的坐标为(6,5)时,∠CDE=90°,CD=2,DE=4,则AB:BC=DE:CD,△EDC∽△ABC,故本选项不符合题意;
D、当点E的坐标为(4,2)时,∠ECD=90°,CD=2,CE=1,则AB:BC=CD:CE,△DCE∽△ABC,故本选项不符合题意;
故选:B.
10.解:三角形纸片ABC中,AB=8,BC=4,AC=6.
A、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B、=,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、==,对应边===,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
故选:D.
11.解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠C=70°,
∴∠BDC=70°时,
∠C=∠C,∠BDC=∠ABC,
∴△ABC∽△BDC.
故答案为:70.
12.解:∵∠COD=∠AOB,
∴只要∠OAB=∠OCD,∠ODC=∠OBA,∠OAB=∠ODC,∠OCD=∠OBA,AB∥CD等等,其中一项符合即可,答案不唯一.
13.解:应该为丙,因为当R在丙的位置时,若设每一个小正方形的边长为1,则△PQR的三边分别为4、2、2.
△ABC的各边分别为2、、.
各边对应成比例且比例相等均为2,则可以得到两三角形相似.
14.解:∵两个三角形的三边分别为1,,和,,2,
∴,
∴两个三角形相似.
故答案为:相似.
15.解:在△CAB与△CDE中,
,
∴△CAB∽△CDE,
∴=,
∴CD CB=CA CE.
故答案为CDE,CA CE.
16.解:∵∠A=∠A′=70°,∠B=30°,∠C′=80°;
∴∠C=80°;
∴∠C=∠C′;
又∵∠A=∠A′,
∴△ABC∽△A′B′C′.
故答案为:相似,两角对应相等的两个三角形相似.
17.解:根据题意得:
当时,△ABC∽△DEF,
即,
解得:x=40.
答案为:40.
18.解:如图所示:
∵等腰△ABC的两边长分别是4和9,4+4<9,
∴等腰△ABC的腰长是9,底边长为4,
∵等腰△DEF的腰长为6,
∴当时,△ABC∽△DEF,
即,
∴EF=,
即等腰△DEF的腰长为6,则当它的底边长为时,等腰△ABC和等腰△DEF相似;
故答案为:.
19.证明:∵AB=AC,
∴∠B=∠C,
∵∠BAE=∠BAD+∠DAE,∠CDA=∠BAD+∠B,
又∵∠DAE=∠B,
∴∠BAE=∠CDA,
∴△ABE∽△DCA.
20.证明:∵AD是△ABC的高,E、F分别是AB、AC的中点,
∴DE=AB,DF=AC,EF是△ABC的中位线,
∴EF=BC,
∴===,
∴△DEF∽△ABC.
21.解:设经过t秒,后以A,P,E为顶点的三角形和△ABC相似.
①当△AEP∽△ABC时,=,即=,
解得t=;
②当△APE∽△ABC时,=,即=,
解得t=;
综上所述,经或秒后以A,P,E为顶点的三角形和△ABC相似.
如果点E改为C出发向点B运动,由于△APE不是直角三角形,所以这两个三角形不可能相似.
1.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
2.如图,网格中每个小正方形的边长均为1,则图中与阴影三角形相似的三角形是( )
A.A B.B C.C D.D
3.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
4.如图,△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为( )
A.4个 B.3个 C.2个 D.1个
5.如图,下列条件中,不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B.∠B=∠ACD C.∠ACD=∠BCD D.
6.下列说法错误的是( )
A.两个等边三角形一定相似 B.两个等腰三角形一定相似
C.两个等腰直角三角形一定相似 D.两个全等三角形一定相似
7.如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
8.下列各组图形中可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
9.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
10.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
11.如图,在△ABC中,AB=AC,∠BAC=40°,点D是AC的动点,当∠BDC= °时,△ABC∽△BDC.
12.如图,线段AC、BD交于点O,请你添加一个条件: ,使△AOB∽△COD.
13.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲乙丙丁四点中的 .
14.已知两个三角形的三边分别为1,,和,,2,则两个三角形 .(填”相似”或“不相似”)
15.如图,若AB⊥BC,DE⊥AC,则△CAB∽△ ,CD CB= .
16.在△ABC和△A′B′C′中,∠A=∠A′=70°,∠B=30°,∠C′=80°,则这两个三角形 (填“相似”或“不相似”),理由是 .
17.如图所示,要使△ABC∽△DEF,则x= .
18.已知等腰△ABC的两边长分别是4和9,等腰△DEF的腰长为6,则当它的底边长为 时,等腰△ABC和等腰△DEF相似.
19.已知:如图,AB=AC,∠DAE=∠B,求证:△ABE∽△DCA.
20.如图,AD是△ABC的高,E、F分别是AB的、AC的中点.求证:△DEF∽△ABC.
21.如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
参考答案
1.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
2.解:阴影三角形两直角边长分别为2和3,
(A)该直角三角形的两直角边长分别为3和4,且≠,故不能与阴影三角形相似.
(B)该直角三角形的两直角边长分别为4和5,且,故不能与阴影三角形相似.
(C)该直角三角形的两直角边长分别为4和6,且=,故能与阴影三角形相似.
(D)该三角形的三边长分别为、、,不是直角三角形,故不能与阴影三角形相似.
故选:C.
3.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
4.解:∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC,
∵∠1=∠3,∠A=∠A,
∴△ADE∽△ACD,
∴图中与△ADE相似的三角形有2个.
故选:C.
5.解:(A)∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故A能判定△ACD∽△ABC;
(B)∵∠A=∠A,∠B=∠ACD,
∴△ACD∽△ABC,故B能判定△ACD∽△ABC;
(D)∵=,∠A=∠A,
∴△ACD∽△ABC,故D能判定△ACD∽△ABC;
故选:C.
6.解:A、两个等边三角形一定相似,所以A选项的说法正确;
B、两个等腰三角形不一定相似,如等边三角形与等腰直角三角形不相似,所以B选项的说法错误;
C、两个等腰直角三角形一定相似,所以C选项的说法正确;
D、两个全边三角形一定相似,所以D选项的说法正确.
故选:B.
7.
解:∵截得的小三角形与△ABC相似,
∴过P作AC的垂线,作AB的垂线,作BC的垂线,所截得的三角形满足题意,
则D点的位置最多有3处,
故选:B.
8.解:A、不正确,因为没有指明这个45°的角是顶角还是底角,则无法判定其相似;
B、由已知我们可以得到这是两个正三角形,从而可以根据三组对应边的比相等的两个三角形相似判定这两个三角形相似;
C、正确,已知一个角为105°,则我们可以判定其为顶角,这样我们就可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似判定这两个三角形相似;
D、正确,因为是等腰直角三角形,则我们可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定这两个三角形相似.
故选:A.
9.解:△ABC中,∠ABC=90°,AB=6,BC=3,AB:BC=2.
A、当点E的坐标为(6,0)时,∠CDE=90°,CD=2,DE=1,则AB:BC=CD:DE,△CDE∽△ABC,故本选项不符合题意;
B、当点E的坐标为(6,3)时,∠CDE=90°,CD=2,DE=2,则AB:BC≠CD:DE,△CDE与△ABC不相似,故本选项符合题意;
C、当点E的坐标为(6,5)时,∠CDE=90°,CD=2,DE=4,则AB:BC=DE:CD,△EDC∽△ABC,故本选项不符合题意;
D、当点E的坐标为(4,2)时,∠ECD=90°,CD=2,CE=1,则AB:BC=CD:CE,△DCE∽△ABC,故本选项不符合题意;
故选:B.
10.解:三角形纸片ABC中,AB=8,BC=4,AC=6.
A、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B、=,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、==,对应边===,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
故选:D.
11.解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠C=70°,
∴∠BDC=70°时,
∠C=∠C,∠BDC=∠ABC,
∴△ABC∽△BDC.
故答案为:70.
12.解:∵∠COD=∠AOB,
∴只要∠OAB=∠OCD,∠ODC=∠OBA,∠OAB=∠ODC,∠OCD=∠OBA,AB∥CD等等,其中一项符合即可,答案不唯一.
13.解:应该为丙,因为当R在丙的位置时,若设每一个小正方形的边长为1,则△PQR的三边分别为4、2、2.
△ABC的各边分别为2、、.
各边对应成比例且比例相等均为2,则可以得到两三角形相似.
14.解:∵两个三角形的三边分别为1,,和,,2,
∴,
∴两个三角形相似.
故答案为:相似.
15.解:在△CAB与△CDE中,
,
∴△CAB∽△CDE,
∴=,
∴CD CB=CA CE.
故答案为CDE,CA CE.
16.解:∵∠A=∠A′=70°,∠B=30°,∠C′=80°;
∴∠C=80°;
∴∠C=∠C′;
又∵∠A=∠A′,
∴△ABC∽△A′B′C′.
故答案为:相似,两角对应相等的两个三角形相似.
17.解:根据题意得:
当时,△ABC∽△DEF,
即,
解得:x=40.
答案为:40.
18.解:如图所示:
∵等腰△ABC的两边长分别是4和9,4+4<9,
∴等腰△ABC的腰长是9,底边长为4,
∵等腰△DEF的腰长为6,
∴当时,△ABC∽△DEF,
即,
∴EF=,
即等腰△DEF的腰长为6,则当它的底边长为时,等腰△ABC和等腰△DEF相似;
故答案为:.
19.证明:∵AB=AC,
∴∠B=∠C,
∵∠BAE=∠BAD+∠DAE,∠CDA=∠BAD+∠B,
又∵∠DAE=∠B,
∴∠BAE=∠CDA,
∴△ABE∽△DCA.
20.证明:∵AD是△ABC的高,E、F分别是AB、AC的中点,
∴DE=AB,DF=AC,EF是△ABC的中位线,
∴EF=BC,
∴===,
∴△DEF∽△ABC.
21.解:设经过t秒,后以A,P,E为顶点的三角形和△ABC相似.
①当△AEP∽△ABC时,=,即=,
解得t=;
②当△APE∽△ABC时,=,即=,
解得t=;
综上所述,经或秒后以A,P,E为顶点的三角形和△ABC相似.
如果点E改为C出发向点B运动,由于△APE不是直角三角形,所以这两个三角形不可能相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
