第4章图形的相似 同步达标测评 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第4章图形的相似 同步达标测评 2021-2022学年北师大版九年级数学上册(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 308.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 00:00:00 | ||
图片预览


文档简介
2021-2022北师大版九年级数学上册《第4章图形的相似》同步达标测评(附答案)
一.选择题(共12小题,满分36分)
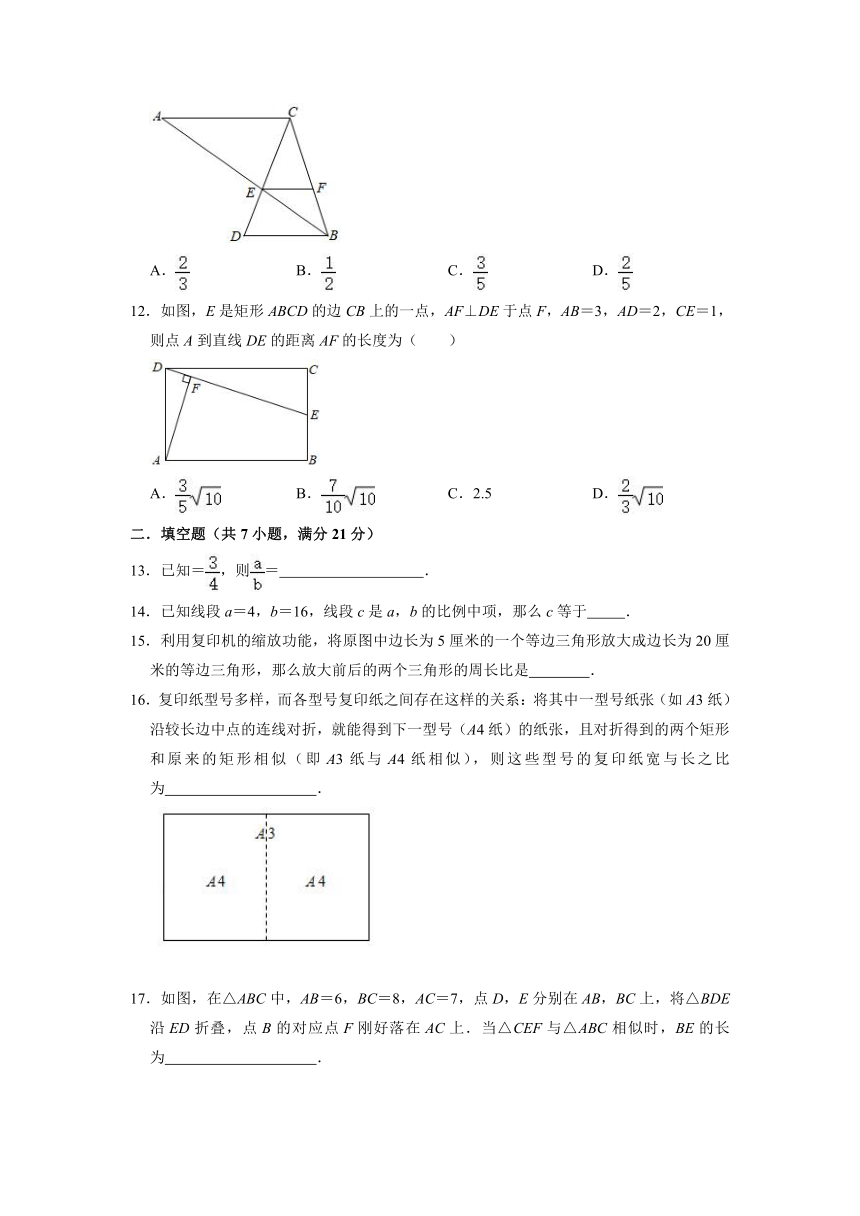
1.若x﹣3y=0且y≠0,则的值为( )
A.11 B.﹣ C. D.﹣11
2.若=,则的值为( )
A.5 B. C.3 D.
3.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
4.如图,下面图形及各个选项均是由边长为1的小方格组成的网格,三角形的顶点均在小方格的顶点上,下列四个选项中哪一个阴影部分的三角形与已知△ABC相似( )
A.B.C.D.
5.在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
6.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,点H为AF与DG的交点.若AC=9,则DH为( )
A.1 B.2 C. D.3
7.如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
8.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
9.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形ABCD的边长为2,则点F坐标为( )
A.(8,6) B.(9,6) C. D.(10,6)
10.若△ABC的每条边长增加各自的20%得△A'B'C',则∠B'的度数与其对应角∠B的度数相比( )
A.增加了20% B.减少了20%
C.增加了(1+20%) D.没有改变
11.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
12.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,则点A到直线DE的距离AF的长度为( )
A. B. C.2.5 D.
二.填空题(共7小题,满分21分)
13.已知=,则= .
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
15.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
16.复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为 .
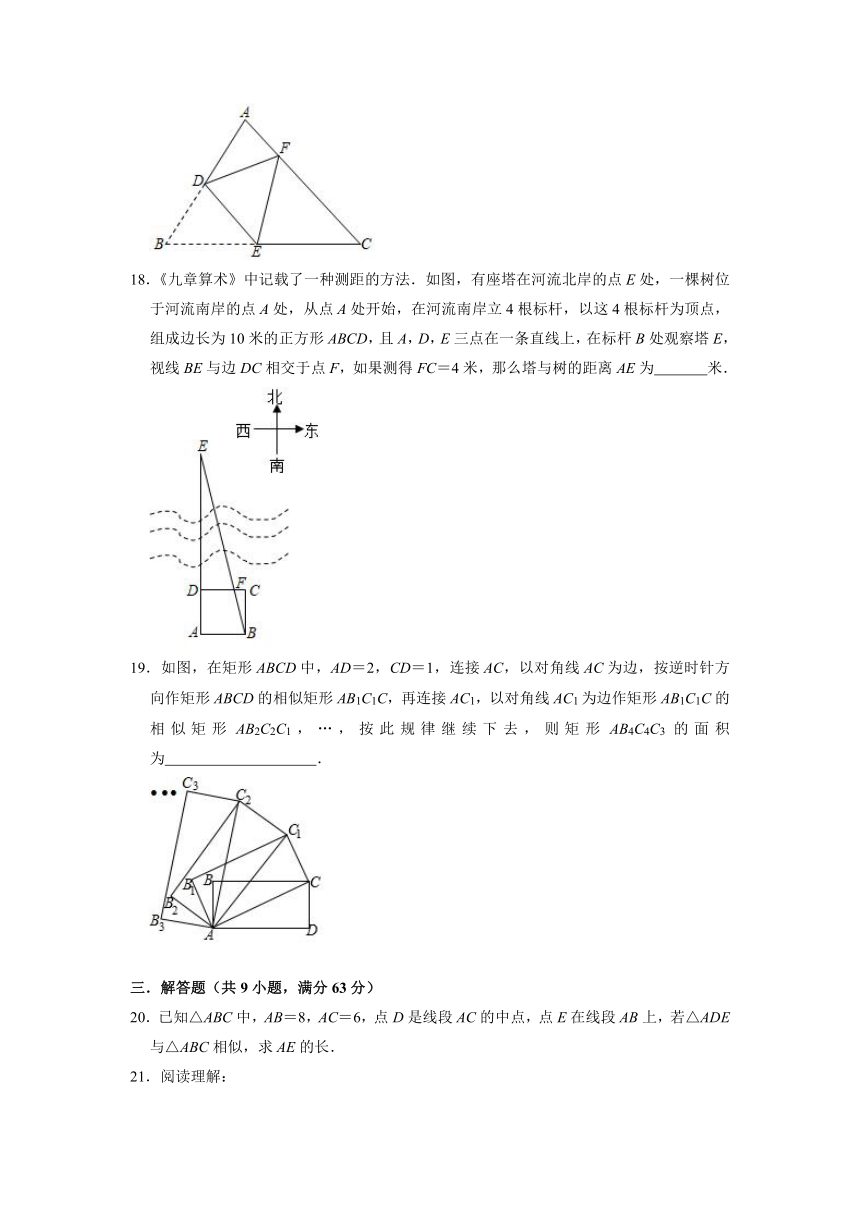
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
18.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得FC=4米,那么塔与树的距离AE为 米.
19.如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB4C4C3的面积为 .
三.解答题(共9小题,满分63分)
20.已知△ABC中,AB=8,AC=6,点D是线段AC的中点,点E在线段AB上,若△ADE与△ABC相似,求AE的长.
21.阅读理解:
已知:a,b,c,d都是不为0的数,且=,求证:=.
证明:∵=,
∴+1=+1.
∴=.
根据以上方法,解答下列问题:
(1)若=,求的值;
(2)若=,且a≠b,c≠d,证明=.
22.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
23.如图,在△ABC中,四边形DBFE是平行四边形.求证:△ADE∽△EFC.
24.如图,在平面直角坐标系中,△ABC的顶点A的坐标为(﹣3,﹣1),顶点B,C都在小正方形的格点上.
(1)点B的坐标为 ,点C的坐标为 .
(2)以原点O为位似中心,在所给的网格中画出一个△A1B1C1,使得△A1B1C1与△ABC位似,且相似比为2:1.
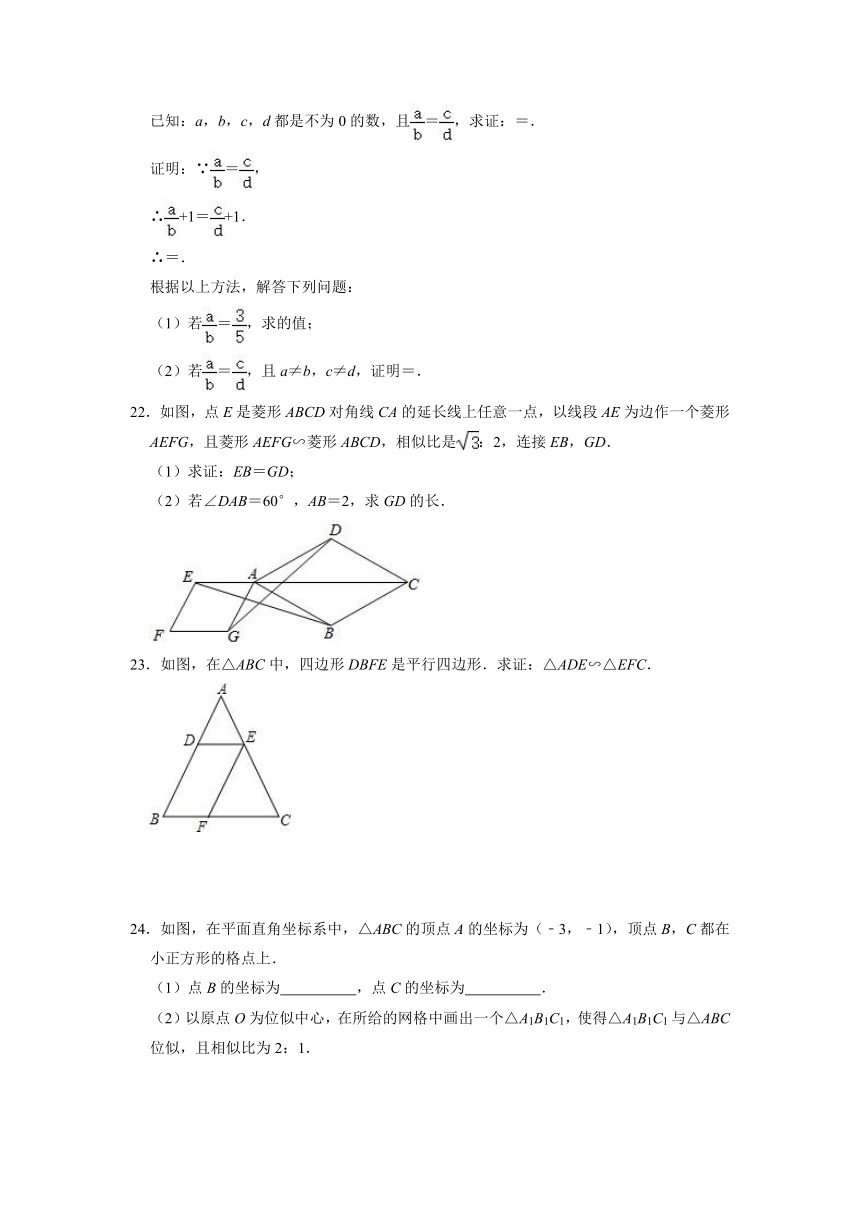
25.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
26.如图,在矩形ABCD中,E是CD上一点,AE=AB,作BF⊥AE.
(1)求证:△ADE≌△BFA;
(2)连接BE,若△BCE与△ADE相似,求.
27.已知:正方形ABCD,GF∥BE,求证:EF AE=BE EC.
28.如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
参考答案
一.选择题(共12小题,满分36分)
1.解:∵x﹣3y=0且y≠0,
∴x=3y,
∴==.
故选:C.
2.解:由=,得
4b=a﹣b.,解得a=5b,
==5,
故选:A.
3.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
4.解:根据题意得:AC==,AB==,BC=1,
∴BC:AB:AC=1::,
A、三边之比为1::,选项A符合题意;
B、三边之比::3,选项B不符合题意;
C、三边之比为2::,选项C不符合题意;
D、三边之比为::4,选项D不符合题意.
故选:A.
5.解:由题意得DE为△ABC的中位线,那么DE∥BC,DE:BC=1:2.
∴△ADE∽△ABC
∴△ADE与△ABC的周长之比为1:2,
∴△ADE与△ABC的面积之比为1:4,即.
故选:B.
6.解:∵D、E为边AB的三等分点,EF∥DG∥AC,
∴BE=DE=AD,BF=GF=CG,AH=HF,
∴AB=3BE,DH是△AEF的中位线,
∴DH=EF,
∵EF∥AC,
∴△BEF∽△BAC,
∴=,即 =,
解得:EF=3,
∴DH=EF=×3=,
故选:C.
7.解:设旗杆高度为h,
由题意得=,h=8米.
故选:C.
8.解:设点B′的横坐标为x,
则B、C间的水平距离为a﹣1,B′、C间的水平距离为﹣x+1,
∵△ABC放大到原来的2倍得到△A′B′C,
∴2(a﹣1)=﹣x+1,
解得:x=﹣2a+3,
故选:A.
9.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴==,
∵BC=2,
∴EF=BE=6,
∵BC∥EF,
∴△OBC∽△OEF,
∴=,
解得:OB=3,
∴EO=9,
∴F点坐标为:(9,6),
故选:B.
10.解:∵△ABC的每条边长增加各自的20%得△A′B′C′,
∴△ABC与△A′B′C′的三边对应成比例,
∴△ABC∽△A′B′C′,
∴∠B′=∠B.
故选:D.
11.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
12.解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,CD=AB=3,BC=AD=2,
∴DE===,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴∠DAF+∠ADF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∴△ADF∽△DCE,
∴=,
∴=,
∴AF=.
故选:A.
二.填空题(共7小题,满分21分)
13.解:∵=,
∴=,
∴﹣=,
∴=.
故答案为:.
14.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
15.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
16.解:设这些型号的复印纸的长、宽分别为b、a,
∵得到的矩形都和原来的矩形相似,
∴=,则b2=2a2,
∴=,
故答案为:.
17.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
18.解:∵四边形ABCD是正方形,边长为10米,
∴AD=CD=BC=10米,FD=CD﹣CF=6米,BC∥AD,
∴△FDE∽△FCB,
∴,即,
∴DE=15,
∴AE=DE+AD=25米,
故答案为:25.
19.解:∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC===,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积=,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=
∴矩形AB3C3C2的面积=,
按此规律第4个矩形的面积为,
故答案为:.
三.解答题(共9小题,满分63分)
20.解:∵点D是线段AC的中点,
∴AD=AC=3.
∵△ADE与△ABC相似,
当时,
即,
解得AE=.
当时,
即,
解得:AE=4,
综上所述,AE的值为4或.
21.解:(1)∵=,
∴=+1=+1=.
(2)∵=,
∴﹣1=﹣1,
∴=,
∵=,
∴÷=÷,
∴=.
22.(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∵菱形AEFG∽菱形ABCD,相似比是:2,AB=2,
∴AE=,BP=AB=1,
∴AP=,
∴EP=,
∴EB=,
∴GD=.
23.证明:∵四边形DBFE是平行四边形,
∴DE∥BC,EF∥AB,
∴∠CEF=∠A,∠AED=∠C,
∴△ADE∽△EFC.
24.解:(1)由题意B(1,2),C(﹣2,3),
故答案为:(1,2),(﹣2,3).
(2)如图,△A1B1C1即为所求作.
25.解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
26.(1)证明:∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,
∴∠DAE+∠FAB=90°,
∵BF⊥AE,
∴∠AFB=90°,
∴∠D=∠AFB,∠FBA+∠FAB=90°,
∴∠DAE=∠FBA,
在△ADE和△BFA中
,
∴△ADE≌△BFA(AAS);
(2)解:∵四边形ABCD是矩形,
∴∠C=∠D=90°,DC∥AB,
∴∠CEB=∠ABE,
设∠CEB=∠ABE=x°,
∵AE=AB,
∴∠AEB=∠EBA=x°,
当△BCE与△ADE相似时,有两种情况:
①∠DEA=∠CEB=x°,
∵∠DEA+∠AEB+∠CEB=180°,
∴x+x+x=180,
解得:x=60,
即∠DEA=60°,
∴∠DAE=90°﹣60°=30°,
∴AE=2DE,由勾股定理得:AD===DE,
∵AE=AB,
∴===;
②∠DEA=∠EBC,
设∠DEA=∠EBC=y°,
∵∠CEB=∠EBA=∠AEB=x°,
则∠DEA+∠AEB+∠CEB=y°+x°+x°=(y+2x)°=180°,
在Rt△BCE中,∠EBC+∠CEB=y°+x°=(y+x)°=90°,
即,
解得:x=90°,
即∠CEB=90°,
此时点E和点C重合,△BEC不存在,舍去;
所以=.
27.证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∵GF∥BE,
∴GF∥CD,
∴,
同理:,
∴,
∴EF AE=BE EC.
28.解:∵∠C=90°,BC=8cm,AC:AB=3:5,
∴设AC=3xcm,AB=5xcm,
则BC==4x(cm),
即4x=8,
解得:x=2,
∴AC=6cm,AB=10cm,
∴BC=8cm,
设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,
则BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,
∵∠C是公共角,
∴①当,即时,△CPQ∽△CBA,
解得:t=2.4,
②当,即时,△CPQ∽△CAB,
解得:t=,
∴过2.4或秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
一.选择题(共12小题,满分36分)
1.若x﹣3y=0且y≠0,则的值为( )
A.11 B.﹣ C. D.﹣11
2.若=,则的值为( )
A.5 B. C.3 D.
3.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
4.如图,下面图形及各个选项均是由边长为1的小方格组成的网格,三角形的顶点均在小方格的顶点上,下列四个选项中哪一个阴影部分的三角形与已知△ABC相似( )
A.B.C.D.
5.在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
6.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,点H为AF与DG的交点.若AC=9,则DH为( )
A.1 B.2 C. D.3
7.如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
8.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
9.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形ABCD的边长为2,则点F坐标为( )
A.(8,6) B.(9,6) C. D.(10,6)
10.若△ABC的每条边长增加各自的20%得△A'B'C',则∠B'的度数与其对应角∠B的度数相比( )
A.增加了20% B.减少了20%
C.增加了(1+20%) D.没有改变
11.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
12.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,则点A到直线DE的距离AF的长度为( )
A. B. C.2.5 D.
二.填空题(共7小题,满分21分)
13.已知=,则= .
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
15.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
16.复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为 .
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
18.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得FC=4米,那么塔与树的距离AE为 米.
19.如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB4C4C3的面积为 .
三.解答题(共9小题,满分63分)
20.已知△ABC中,AB=8,AC=6,点D是线段AC的中点,点E在线段AB上,若△ADE与△ABC相似,求AE的长.
21.阅读理解:
已知:a,b,c,d都是不为0的数,且=,求证:=.
证明:∵=,
∴+1=+1.
∴=.
根据以上方法,解答下列问题:
(1)若=,求的值;
(2)若=,且a≠b,c≠d,证明=.
22.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
23.如图,在△ABC中,四边形DBFE是平行四边形.求证:△ADE∽△EFC.
24.如图,在平面直角坐标系中,△ABC的顶点A的坐标为(﹣3,﹣1),顶点B,C都在小正方形的格点上.
(1)点B的坐标为 ,点C的坐标为 .
(2)以原点O为位似中心,在所给的网格中画出一个△A1B1C1,使得△A1B1C1与△ABC位似,且相似比为2:1.
25.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
26.如图,在矩形ABCD中,E是CD上一点,AE=AB,作BF⊥AE.
(1)求证:△ADE≌△BFA;
(2)连接BE,若△BCE与△ADE相似,求.
27.已知:正方形ABCD,GF∥BE,求证:EF AE=BE EC.
28.如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
参考答案
一.选择题(共12小题,满分36分)
1.解:∵x﹣3y=0且y≠0,
∴x=3y,
∴==.
故选:C.
2.解:由=,得
4b=a﹣b.,解得a=5b,
==5,
故选:A.
3.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
4.解:根据题意得:AC==,AB==,BC=1,
∴BC:AB:AC=1::,
A、三边之比为1::,选项A符合题意;
B、三边之比::3,选项B不符合题意;
C、三边之比为2::,选项C不符合题意;
D、三边之比为::4,选项D不符合题意.
故选:A.
5.解:由题意得DE为△ABC的中位线,那么DE∥BC,DE:BC=1:2.
∴△ADE∽△ABC
∴△ADE与△ABC的周长之比为1:2,
∴△ADE与△ABC的面积之比为1:4,即.
故选:B.
6.解:∵D、E为边AB的三等分点,EF∥DG∥AC,
∴BE=DE=AD,BF=GF=CG,AH=HF,
∴AB=3BE,DH是△AEF的中位线,
∴DH=EF,
∵EF∥AC,
∴△BEF∽△BAC,
∴=,即 =,
解得:EF=3,
∴DH=EF=×3=,
故选:C.
7.解:设旗杆高度为h,
由题意得=,h=8米.
故选:C.
8.解:设点B′的横坐标为x,
则B、C间的水平距离为a﹣1,B′、C间的水平距离为﹣x+1,
∵△ABC放大到原来的2倍得到△A′B′C,
∴2(a﹣1)=﹣x+1,
解得:x=﹣2a+3,
故选:A.
9.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴==,
∵BC=2,
∴EF=BE=6,
∵BC∥EF,
∴△OBC∽△OEF,
∴=,
解得:OB=3,
∴EO=9,
∴F点坐标为:(9,6),
故选:B.
10.解:∵△ABC的每条边长增加各自的20%得△A′B′C′,
∴△ABC与△A′B′C′的三边对应成比例,
∴△ABC∽△A′B′C′,
∴∠B′=∠B.
故选:D.
11.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
12.解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,CD=AB=3,BC=AD=2,
∴DE===,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴∠DAF+∠ADF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∴△ADF∽△DCE,
∴=,
∴=,
∴AF=.
故选:A.
二.填空题(共7小题,满分21分)
13.解:∵=,
∴=,
∴﹣=,
∴=.
故答案为:.
14.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
15.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
16.解:设这些型号的复印纸的长、宽分别为b、a,
∵得到的矩形都和原来的矩形相似,
∴=,则b2=2a2,
∴=,
故答案为:.
17.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
18.解:∵四边形ABCD是正方形,边长为10米,
∴AD=CD=BC=10米,FD=CD﹣CF=6米,BC∥AD,
∴△FDE∽△FCB,
∴,即,
∴DE=15,
∴AE=DE+AD=25米,
故答案为:25.
19.解:∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC===,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积=,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=
∴矩形AB3C3C2的面积=,
按此规律第4个矩形的面积为,
故答案为:.
三.解答题(共9小题,满分63分)
20.解:∵点D是线段AC的中点,
∴AD=AC=3.
∵△ADE与△ABC相似,
当时,
即,
解得AE=.
当时,
即,
解得:AE=4,
综上所述,AE的值为4或.
21.解:(1)∵=,
∴=+1=+1=.
(2)∵=,
∴﹣1=﹣1,
∴=,
∵=,
∴÷=÷,
∴=.
22.(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∵菱形AEFG∽菱形ABCD,相似比是:2,AB=2,
∴AE=,BP=AB=1,
∴AP=,
∴EP=,
∴EB=,
∴GD=.
23.证明:∵四边形DBFE是平行四边形,
∴DE∥BC,EF∥AB,
∴∠CEF=∠A,∠AED=∠C,
∴△ADE∽△EFC.
24.解:(1)由题意B(1,2),C(﹣2,3),
故答案为:(1,2),(﹣2,3).
(2)如图,△A1B1C1即为所求作.
25.解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
26.(1)证明:∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,
∴∠DAE+∠FAB=90°,
∵BF⊥AE,
∴∠AFB=90°,
∴∠D=∠AFB,∠FBA+∠FAB=90°,
∴∠DAE=∠FBA,
在△ADE和△BFA中
,
∴△ADE≌△BFA(AAS);
(2)解:∵四边形ABCD是矩形,
∴∠C=∠D=90°,DC∥AB,
∴∠CEB=∠ABE,
设∠CEB=∠ABE=x°,
∵AE=AB,
∴∠AEB=∠EBA=x°,
当△BCE与△ADE相似时,有两种情况:
①∠DEA=∠CEB=x°,
∵∠DEA+∠AEB+∠CEB=180°,
∴x+x+x=180,
解得:x=60,
即∠DEA=60°,
∴∠DAE=90°﹣60°=30°,
∴AE=2DE,由勾股定理得:AD===DE,
∵AE=AB,
∴===;
②∠DEA=∠EBC,
设∠DEA=∠EBC=y°,
∵∠CEB=∠EBA=∠AEB=x°,
则∠DEA+∠AEB+∠CEB=y°+x°+x°=(y+2x)°=180°,
在Rt△BCE中,∠EBC+∠CEB=y°+x°=(y+x)°=90°,
即,
解得:x=90°,
即∠CEB=90°,
此时点E和点C重合,△BEC不存在,舍去;
所以=.
27.证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∵GF∥BE,
∴GF∥CD,
∴,
同理:,
∴,
∴EF AE=BE EC.
28.解:∵∠C=90°,BC=8cm,AC:AB=3:5,
∴设AC=3xcm,AB=5xcm,
则BC==4x(cm),
即4x=8,
解得:x=2,
∴AC=6cm,AB=10cm,
∴BC=8cm,
设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,
则BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,
∵∠C是公共角,
∴①当,即时,△CPQ∽△CBA,
解得:t=2.4,
②当,即时,△CPQ∽△CAB,
解得:t=,
∴过2.4或秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
