2021-2022学年数学苏教版(2019)必修第一册5.1函数的概念和图象第3课时教案(表格式)
文档属性
| 名称 | 2021-2022学年数学苏教版(2019)必修第一册5.1函数的概念和图象第3课时教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 85.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 00:00:00 | ||
图片预览


文档简介
丰县华山中学高一数学组教案
课题 第3课时 函数的概念和图象(3) 编制人: 审核人:
教学目标 1. 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用.2. 通过函数的图象,从“形”的角度进一步加深对函数概念的理解,认识图象法也是描述两个变量之间函数关系的一种重要方法.
教学重点 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用
教学难点 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用
核心素养
授课方法 讲练结合 教学辅助手段 教学多媒体
教师活动 学生活动 二次备课
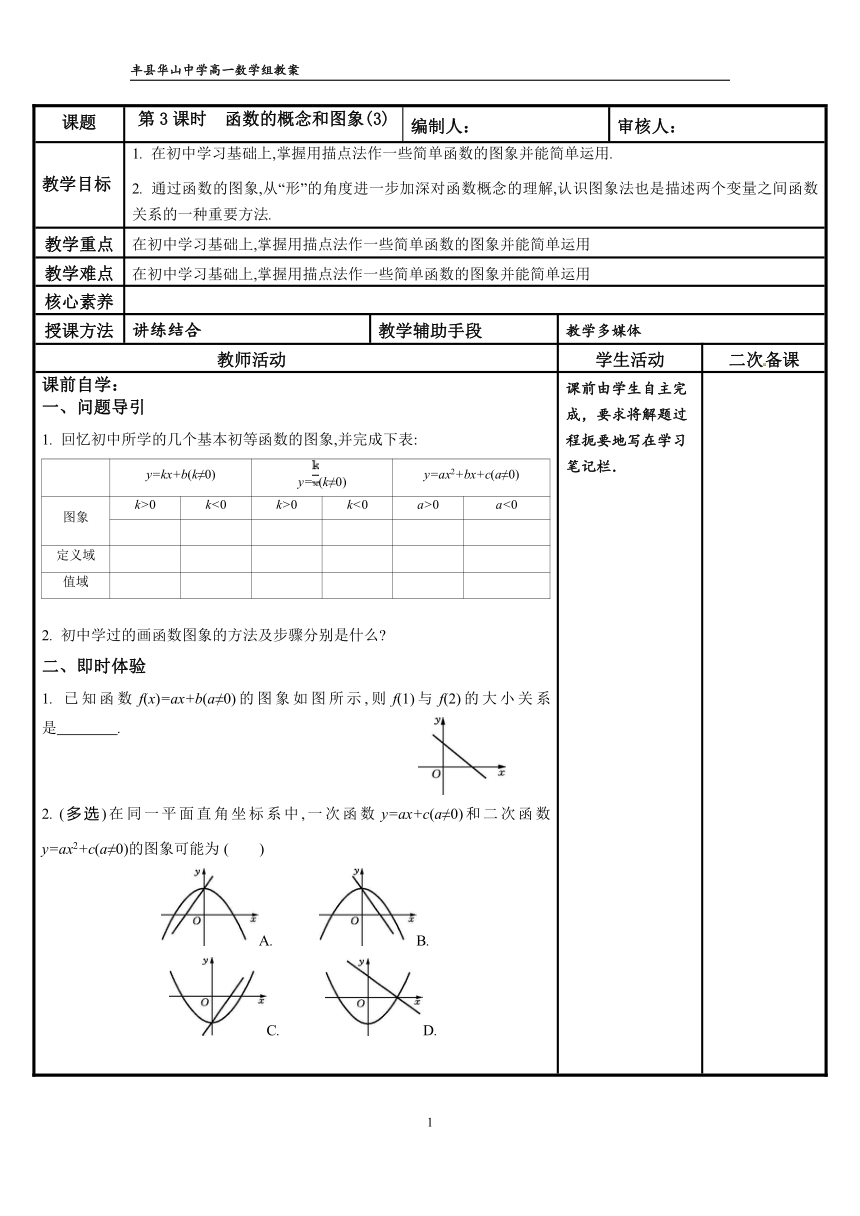
课前自学:一、问题导引1. 回忆初中所学的几个基本初等函数的图象,并完成下表:y=kx+b(k≠0)y=(k≠0)y=ax2+bx+c(a≠0)图象k>0k<0k>0k<0a>0a<0定义域值域2. 初中学过的画函数图象的方法及步骤分别是什么 二、即时体验1. 已知函数f(x)=ax+b(a≠0)的图象如图所示,则f(1)与f(2)的大小关系是 . 2. (多选)在同一平面直角坐标系中,一次函数y=ax+c(a≠0)和二次函数y=ax2+c(a≠0)的图象可能为 ( )A. B. C. D. 课前由学生自主完成,要求将解题过程扼要地写在学习笔记栏.
教师活动 学生活动 二次备课
课堂互学、导学、探究、拓展:三、导学过程类型1 画连续型函数的图象【例1】 试画出下列函数的图象:(1) f(x)=x+1; (2) f(x)=(x-1)2+1, x∈[1, 3).类型2 画离散型函数的图象【例2】 画出下列函数的图象:(1) f(x)=5x, x∈{1, 2, 3}; (2) f(x)=x2, x∈{-2, -1, 0, 1, 2}. 例1可让学生先板演,教师再作点评,特别注意解题过程的规范性
教师活动 学生活动 二次备课
类型3 函数图象的简单运用【例3】 试画出二次函数f(x)=x2+1的图象,并根据图象回答下列问题:(1) 比较f(-2), f(1), f(3)的大小;(2) 若0教师活动 学生活动 二次备课
课堂检测:四、课堂练习1. 若把函数f(x)=x2-1的图象作平移变换,使原图象上的点P(1, 0)变换成点Q(2, -1),则变换后所得新图象对应的函数表达式为 . 学生限时完成重点学生板演学生回答结果
作业 预习导学案
教学反思
1
课题 第3课时 函数的概念和图象(3) 编制人: 审核人:
教学目标 1. 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用.2. 通过函数的图象,从“形”的角度进一步加深对函数概念的理解,认识图象法也是描述两个变量之间函数关系的一种重要方法.
教学重点 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用
教学难点 在初中学习基础上,掌握用描点法作一些简单函数的图象并能简单运用
核心素养
授课方法 讲练结合 教学辅助手段 教学多媒体
教师活动 学生活动 二次备课
课前自学:一、问题导引1. 回忆初中所学的几个基本初等函数的图象,并完成下表:y=kx+b(k≠0)y=(k≠0)y=ax2+bx+c(a≠0)图象k>0k<0k>0k<0a>0a<0定义域值域2. 初中学过的画函数图象的方法及步骤分别是什么 二、即时体验1. 已知函数f(x)=ax+b(a≠0)的图象如图所示,则f(1)与f(2)的大小关系是 . 2. (多选)在同一平面直角坐标系中,一次函数y=ax+c(a≠0)和二次函数y=ax2+c(a≠0)的图象可能为 ( )A. B. C. D. 课前由学生自主完成,要求将解题过程扼要地写在学习笔记栏.
教师活动 学生活动 二次备课
课堂互学、导学、探究、拓展:三、导学过程类型1 画连续型函数的图象【例1】 试画出下列函数的图象:(1) f(x)=x+1; (2) f(x)=(x-1)2+1, x∈[1, 3).类型2 画离散型函数的图象【例2】 画出下列函数的图象:(1) f(x)=5x, x∈{1, 2, 3}; (2) f(x)=x2, x∈{-2, -1, 0, 1, 2}. 例1可让学生先板演,教师再作点评,特别注意解题过程的规范性
教师活动 学生活动 二次备课
类型3 函数图象的简单运用【例3】 试画出二次函数f(x)=x2+1的图象,并根据图象回答下列问题:(1) 比较f(-2), f(1), f(3)的大小;(2) 若0
课堂检测:四、课堂练习1. 若把函数f(x)=x2-1的图象作平移变换,使原图象上的点P(1, 0)变换成点Q(2, -1),则变换后所得新图象对应的函数表达式为 . 学生限时完成重点学生板演学生回答结果
作业 预习导学案
教学反思
1
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
