3.1圆柱的认识(课件) 2020-2021学年数学六年级下册 人教版(共41张PPT)
文档属性
| 名称 | 3.1圆柱的认识(课件) 2020-2021学年数学六年级下册 人教版(共41张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 00:00:00 | ||
图片预览



文档简介
(共41张PPT)
第3课时 圆柱的认识
三 圆柱与圆锥
人教版六年级下册
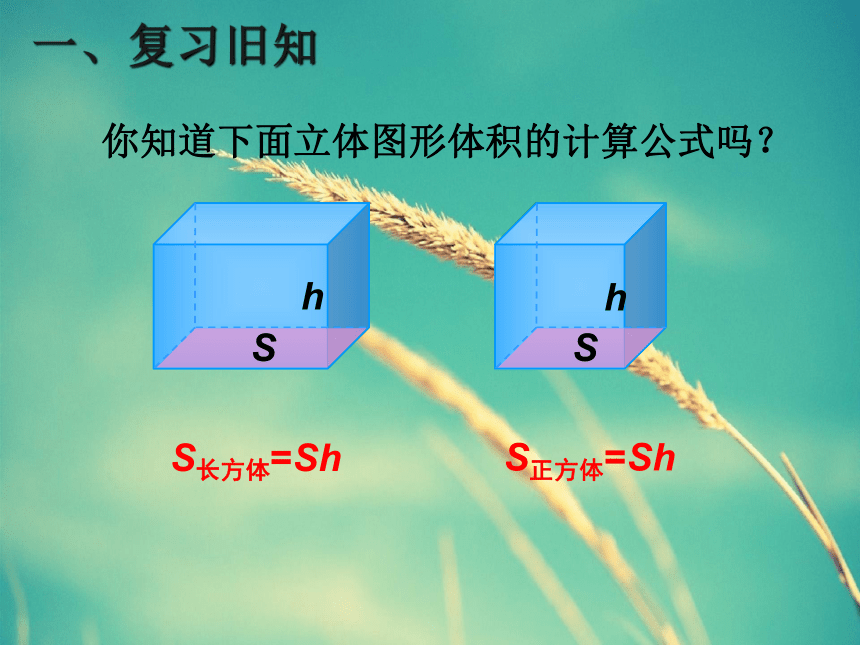
你知道下面立体图形体积的计算公式吗?
S长方体=Sh
S正方体=Sh
h
S
S
h
一、复习旧知
圆柱的体积是什么?
圆柱所占空间的大小叫圆柱的体积。
圆柱的体积又怎么求呢?
二、探究新知--圆柱的体积
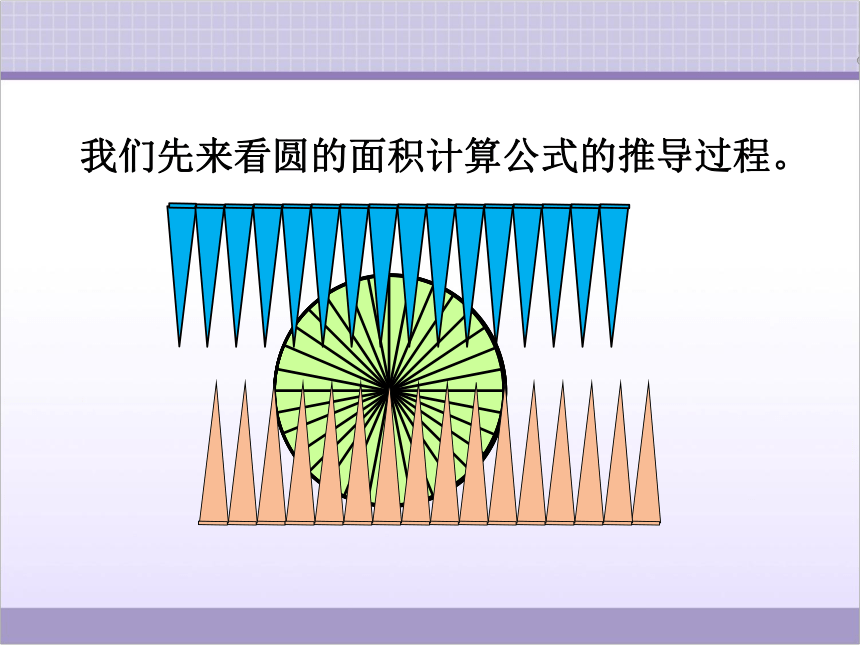
我们先来看圆的面积计算公式的推导过程。
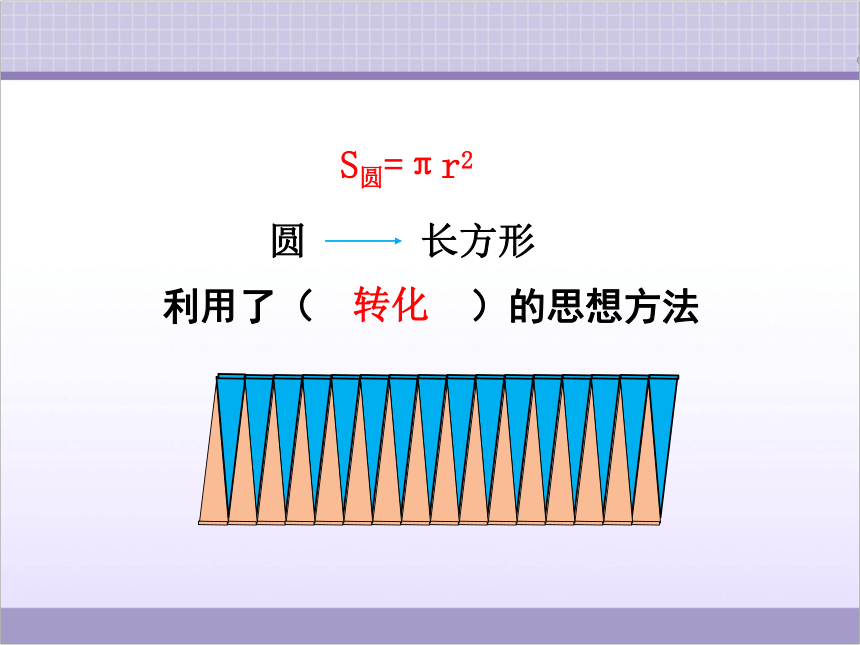
圆
长方形
利用了( )的思想方法
转化
S圆=πr2
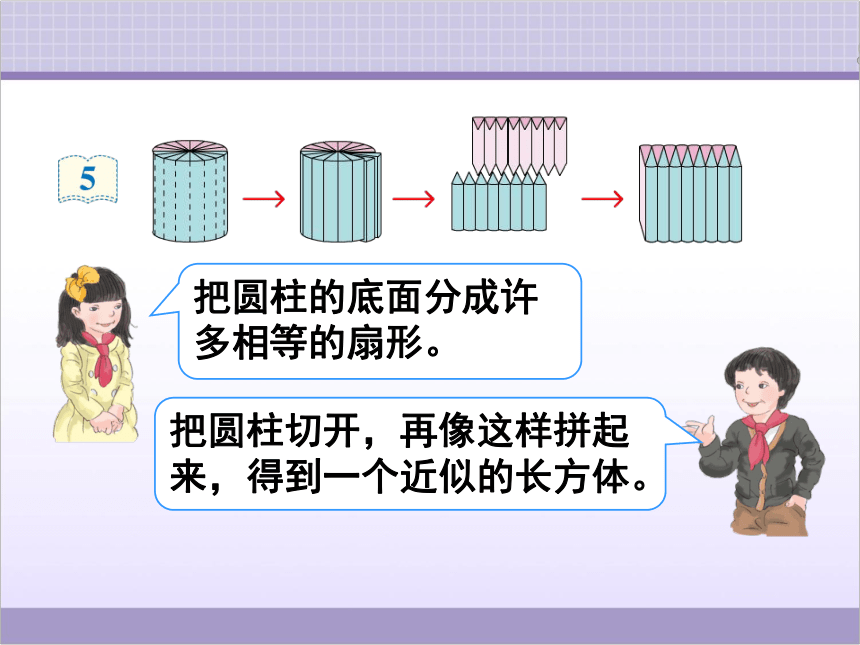
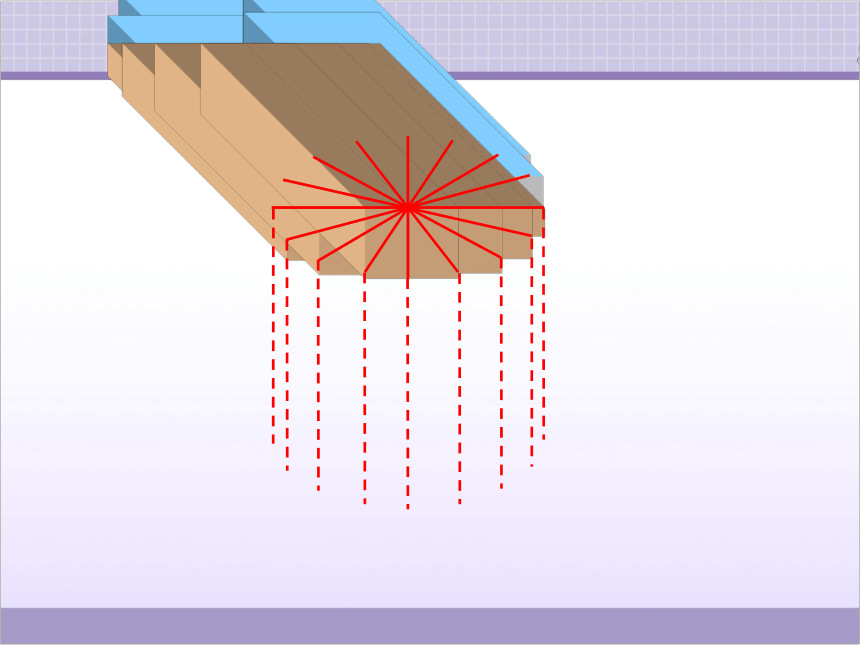
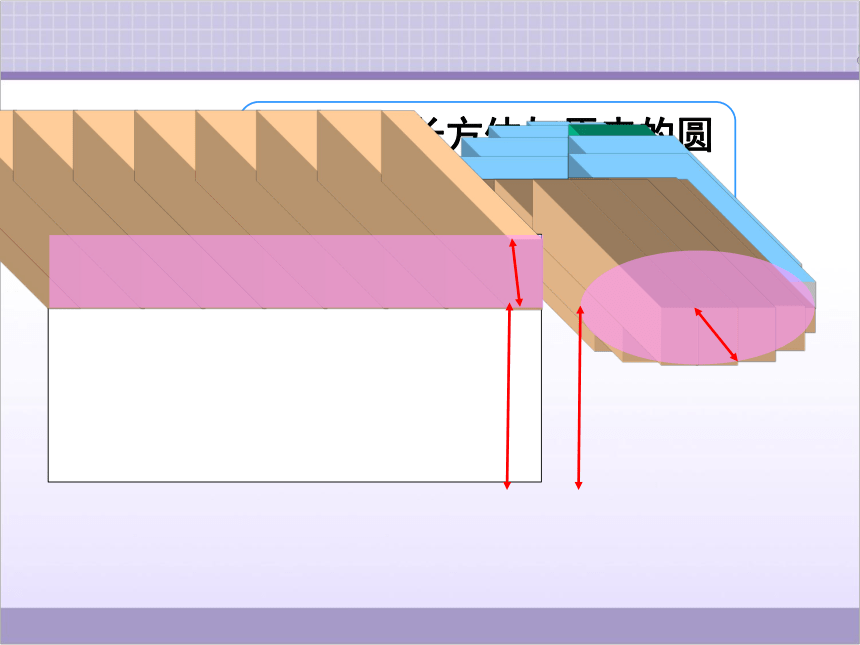
把圆柱的底面分成许多相等的扇形。
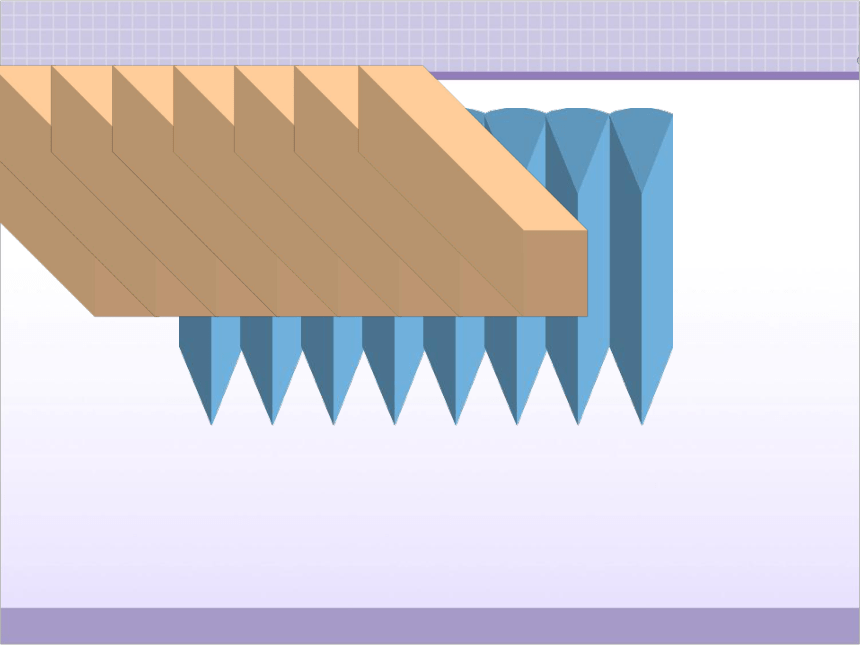
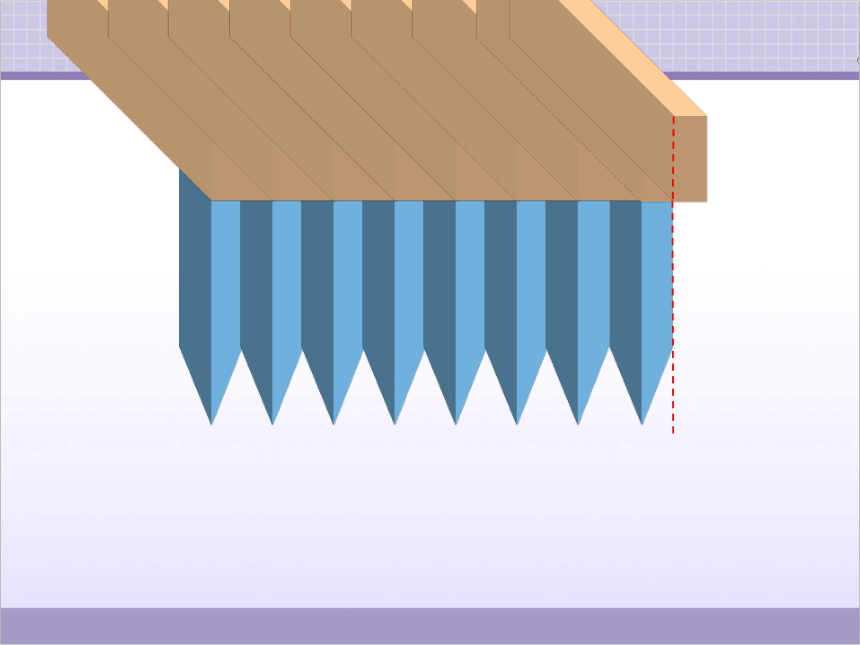
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
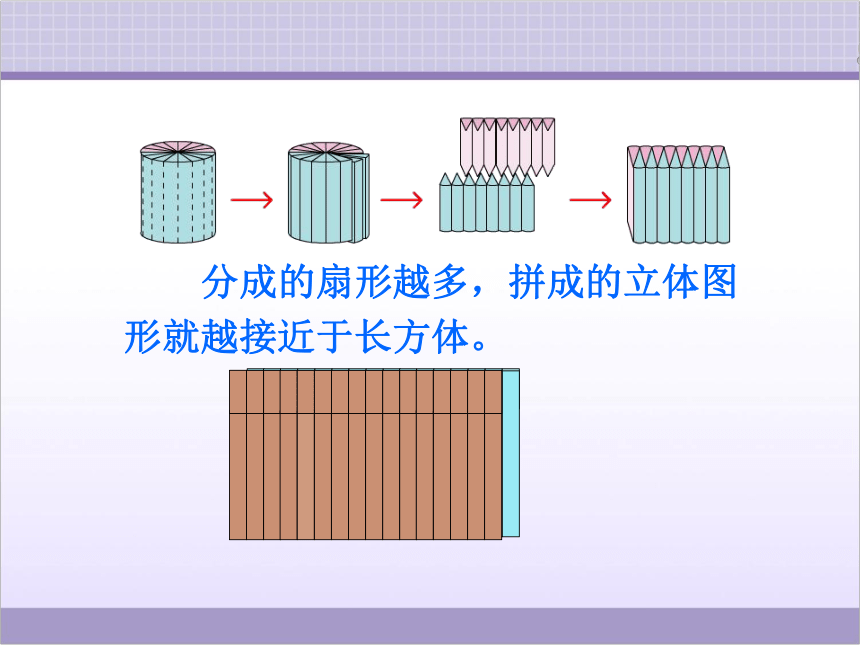
分成的扇形越多,拼成的立体图形就越接近于长方体。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
长方体的高等于圆柱的高。
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S
h
如果知道圆柱的底面半径r和高h
V
圆柱体积计算公式是:
=
πr h
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
1. 如果已知的是底面半径为10厘米,高30厘米,该怎么求它的体积呢?
3.14×102×30=9420(cm3)
答:它的体积是9420cm3。
三、巩固练习
2. 一个圆柱的体积是80cm ,底面积是16cm2。它的高是多少厘米?
80÷16=5(cm)
答:它的高是5㎝。
3. 一个圆柱形木料,底面积为75cm2,长90cm。它的体积是多少?
75×90=6750(cm3)
答:它的体积是6750cm3。
三、巩固练习
4.李家庄挖了一口圆柱形水井,地面以下的井深10m。地面直径为1m。挖出的土有多少立方米?
3.14×(1÷2)2×10=7.85(立方米)
答:挖出的土有7.85立方米。
5.一个圆柱的底面周长是18.84dm,高4dm,这个圆柱的体积是多少?
18.84÷3.14÷2=3(dm)
3.14×32×4=113.04(dm3)
答:这个圆柱的体积是113.04dm3。
6.判断。
(1)圆柱的体积比表面积大。( )
(2)侧面积相等的两个圆柱,它们的体积一定相等。( )
(3)等底等高的正方体、长方体和圆柱的体积都相等。( )
×
×
√
(4)一个圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。
( )
(5)体积相等的两个圆柱不一定等底等高。( )
×
√
长方体的体积=底面积×高
圆柱的体积=底面积×高
V=Sh=πr2h
课堂小结
要先计算出杯子的容积。
请你想一想,要回答这个问题,先要计算出什么?
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
8cm
10cm
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的容积:50.24×10
=502.4(cm3)
=502.4(mL)
杯子的底面积:3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(cm2)
2
2
四、探究新知--圆柱体积公式的应用
1. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
五、巩固练习
保温杯的底面积:
3.14×(8÷2)2
= 3.14×42
= 3.14×16
= 50.24 (cm2)
保温杯的容积:
50.24×15
=753.6 (cm )
=0.7536(L)
答:因为0.7536小于1,所以带这杯水不够喝。
2.下面哪个杯子里的饮料最多?(玻璃杯壁的厚度忽略不计)
3.14×(8÷2)2×4=200.96(cm3)
3.14×(6÷2)2×7=197.82(cm3)
3.14×(5÷2)2×10=196.25(cm3)
因为200.96>197.82>196.25,所以第一个被子饮料最多。
1.
3.一支牙膏出口处直径为0.6厘米,小林每次刷牙都挤出长度大约是1厘米的牙膏,这支牙膏用了100次。牙膏的体积大约是多少?
3.14×(0.6÷2)2×1×100
=3.14×0.09×1×100
=28.26(cm3)
答:牙膏的体积大约是28.26cm3。
4.把一个棱长6分米的正方体木块,削成一个最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=169.56(dm3)
答:这个圆柱的体积是169.56dm3。
还记得我们是怎样测出这个石块的体积的吗?
3.14×(20÷2)2×15-3.14×(20÷2)2×10=1570(cm3)
六、探究新知--求不规则物体的体积
上面计算石头的体积时,我们用到了转化的方法。将不规则的石头转化成规则的圆柱。
今天,我们用这种方法来解决问题。
这个瓶子不是一个完整的圆柱,无法直接计算容积。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
请你认真阅读,理解一下这道题说的是什么意思。
请你仔细想一想,怎么能计算出瓶子的容积呢?
能不能转化成圆柱呢?
18cm
7cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
让我们一起来分析解答这道题吧。
瓶子倒置后,水的体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成两个圆柱的体积。
18cm
7cm
答:这个瓶子的容积是1256mL。
瓶子的容积: 3.14×(8÷2)×7+3.14×(8÷2)×18
=3.14×16×(7+18)
=3.14×16×25
=1256(cm )
=1256(mL)
2
2
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
让我们回顾反思一下吧!
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
七、巩固练习
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
3.14×(6÷2)2×11
=310.86(mL)
800÷310.86≈2.57
2.57<3
答:不够明明和客人每人一杯。
2. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
答:这块铁块的体积是157cm 。
请你想一想,如何求这块铁块的体积?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
2
3.一个输液瓶中装有100mL药液,每分钟输4mL,下面是5分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
4×5=20(mL)
100-20+60=140(mL)
答:整个输液瓶的容积是140mL。
4.有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
5. 下面4个图形的面积都是36dm2(图中单位:dm)。
用这些图形分别卷成圆柱,哪个圆柱的体积最小?
哪个圆柱的体积最大?你有什么发现?
设π=3
上面4个图形当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
2
2
2
2
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图1
图2
图3
图4
18
12
9
6
2
3
4
6
上面4个图形,当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
请你想一想,上面4个图形当以宽为圆柱底面周长时,
会卷成什么样的圆柱?请你动手试一试。
答:底面半径是0.3dm,高是18dm时,圆柱的体积最小;
底面半径是3dm时,高是2dm时,圆柱的体积最大。
5. 下面4个图形的面积都是36dm2(图中单位:dm)。
用这些图形分别卷成圆柱,哪个圆柱的体积最小?
哪个圆柱的体积最大?你有什么发现?
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
设π=3
2
2
2
2
第3课时 圆柱的认识
三 圆柱与圆锥
人教版六年级下册
你知道下面立体图形体积的计算公式吗?
S长方体=Sh
S正方体=Sh
h
S
S
h
一、复习旧知
圆柱的体积是什么?
圆柱所占空间的大小叫圆柱的体积。
圆柱的体积又怎么求呢?
二、探究新知--圆柱的体积
我们先来看圆的面积计算公式的推导过程。
圆
长方形
利用了( )的思想方法
转化
S圆=πr2
把圆柱的底面分成许多相等的扇形。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
分成的扇形越多,拼成的立体图形就越接近于长方体。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
长方体的高等于圆柱的高。
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S
h
如果知道圆柱的底面半径r和高h
V
圆柱体积计算公式是:
=
πr h
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π 2h
已知底面周长和高:V = π 2h
1. 如果已知的是底面半径为10厘米,高30厘米,该怎么求它的体积呢?
3.14×102×30=9420(cm3)
答:它的体积是9420cm3。
三、巩固练习
2. 一个圆柱的体积是80cm ,底面积是16cm2。它的高是多少厘米?
80÷16=5(cm)
答:它的高是5㎝。
3. 一个圆柱形木料,底面积为75cm2,长90cm。它的体积是多少?
75×90=6750(cm3)
答:它的体积是6750cm3。
三、巩固练习
4.李家庄挖了一口圆柱形水井,地面以下的井深10m。地面直径为1m。挖出的土有多少立方米?
3.14×(1÷2)2×10=7.85(立方米)
答:挖出的土有7.85立方米。
5.一个圆柱的底面周长是18.84dm,高4dm,这个圆柱的体积是多少?
18.84÷3.14÷2=3(dm)
3.14×32×4=113.04(dm3)
答:这个圆柱的体积是113.04dm3。
6.判断。
(1)圆柱的体积比表面积大。( )
(2)侧面积相等的两个圆柱,它们的体积一定相等。( )
(3)等底等高的正方体、长方体和圆柱的体积都相等。( )
×
×
√
(4)一个圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。
( )
(5)体积相等的两个圆柱不一定等底等高。( )
×
√
长方体的体积=底面积×高
圆柱的体积=底面积×高
V=Sh=πr2h
课堂小结
要先计算出杯子的容积。
请你想一想,要回答这个问题,先要计算出什么?
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
8cm
10cm
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的容积:50.24×10
=502.4(cm3)
=502.4(mL)
杯子的底面积:3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(cm2)
2
2
四、探究新知--圆柱体积公式的应用
1. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
五、巩固练习
保温杯的底面积:
3.14×(8÷2)2
= 3.14×42
= 3.14×16
= 50.24 (cm2)
保温杯的容积:
50.24×15
=753.6 (cm )
=0.7536(L)
答:因为0.7536小于1,所以带这杯水不够喝。
2.下面哪个杯子里的饮料最多?(玻璃杯壁的厚度忽略不计)
3.14×(8÷2)2×4=200.96(cm3)
3.14×(6÷2)2×7=197.82(cm3)
3.14×(5÷2)2×10=196.25(cm3)
因为200.96>197.82>196.25,所以第一个被子饮料最多。
1.
3.一支牙膏出口处直径为0.6厘米,小林每次刷牙都挤出长度大约是1厘米的牙膏,这支牙膏用了100次。牙膏的体积大约是多少?
3.14×(0.6÷2)2×1×100
=3.14×0.09×1×100
=28.26(cm3)
答:牙膏的体积大约是28.26cm3。
4.把一个棱长6分米的正方体木块,削成一个最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=169.56(dm3)
答:这个圆柱的体积是169.56dm3。
还记得我们是怎样测出这个石块的体积的吗?
3.14×(20÷2)2×15-3.14×(20÷2)2×10=1570(cm3)
六、探究新知--求不规则物体的体积
上面计算石头的体积时,我们用到了转化的方法。将不规则的石头转化成规则的圆柱。
今天,我们用这种方法来解决问题。
这个瓶子不是一个完整的圆柱,无法直接计算容积。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
请你认真阅读,理解一下这道题说的是什么意思。
请你仔细想一想,怎么能计算出瓶子的容积呢?
能不能转化成圆柱呢?
18cm
7cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
让我们一起来分析解答这道题吧。
瓶子倒置后,水的体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成两个圆柱的体积。
18cm
7cm
答:这个瓶子的容积是1256mL。
瓶子的容积: 3.14×(8÷2)×7+3.14×(8÷2)×18
=3.14×16×(7+18)
=3.14×16×25
=1256(cm )
=1256(mL)
2
2
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
让我们回顾反思一下吧!
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
七、巩固练习
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
3.14×(6÷2)2×11
=310.86(mL)
800÷310.86≈2.57
2.57<3
答:不够明明和客人每人一杯。
2. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
答:这块铁块的体积是157cm 。
请你想一想,如何求这块铁块的体积?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
2
3.一个输液瓶中装有100mL药液,每分钟输4mL,下面是5分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
4×5=20(mL)
100-20+60=140(mL)
答:整个输液瓶的容积是140mL。
4.有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
5. 下面4个图形的面积都是36dm2(图中单位:dm)。
用这些图形分别卷成圆柱,哪个圆柱的体积最小?
哪个圆柱的体积最大?你有什么发现?
设π=3
上面4个图形当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
2
2
2
2
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图1
图2
图3
图4
18
12
9
6
2
3
4
6
上面4个图形,当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
请你想一想,上面4个图形当以宽为圆柱底面周长时,
会卷成什么样的圆柱?请你动手试一试。
答:底面半径是0.3dm,高是18dm时,圆柱的体积最小;
底面半径是3dm时,高是2dm时,圆柱的体积最大。
5. 下面4个图形的面积都是36dm2(图中单位:dm)。
用这些图形分别卷成圆柱,哪个圆柱的体积最小?
哪个圆柱的体积最大?你有什么发现?
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
设π=3
2
2
2
2
