2021-2022学年数学人教A版(2019)必修第一册3.2.1函数的单调性与最值(两课时)课件册(共38张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册3.2.1函数的单调性与最值(两课时)课件册(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 09:39:56 | ||
图片预览







文档简介
(共38张PPT)
3.2.1函数的单调性
第一课时
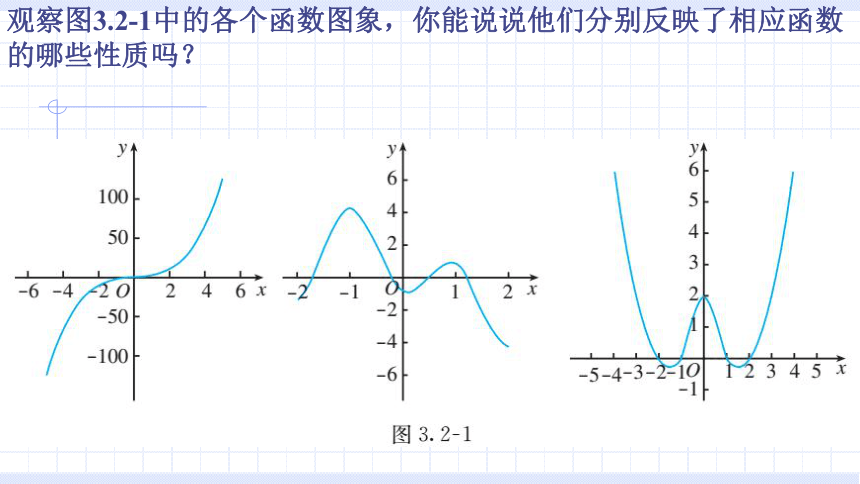
观察图3.2-1中的各个函数图象,你能说说他们分别反映了相应函数的哪些性质吗?
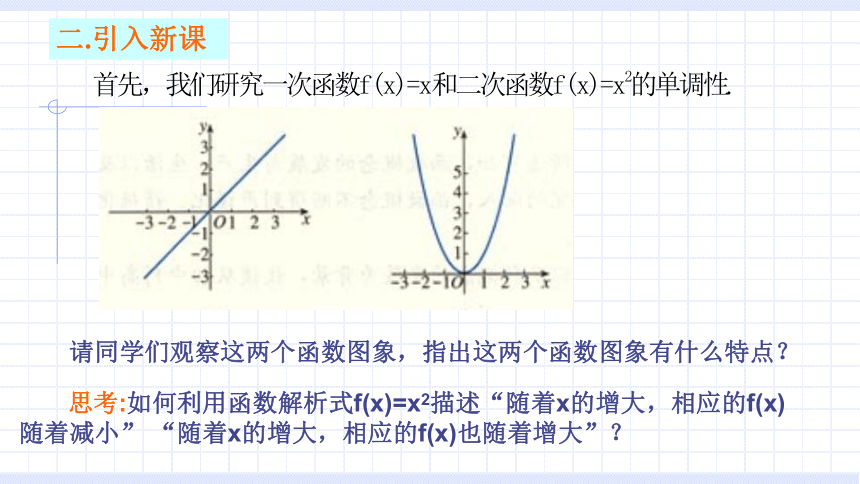
请同学们观察这两个函数图象,指出这两个函数图象有什么特点?
二.引入新课
思考:如何利用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小” “随着x的增大,相应的f(x)也随着增大”?
y
x
O
x0
-x0
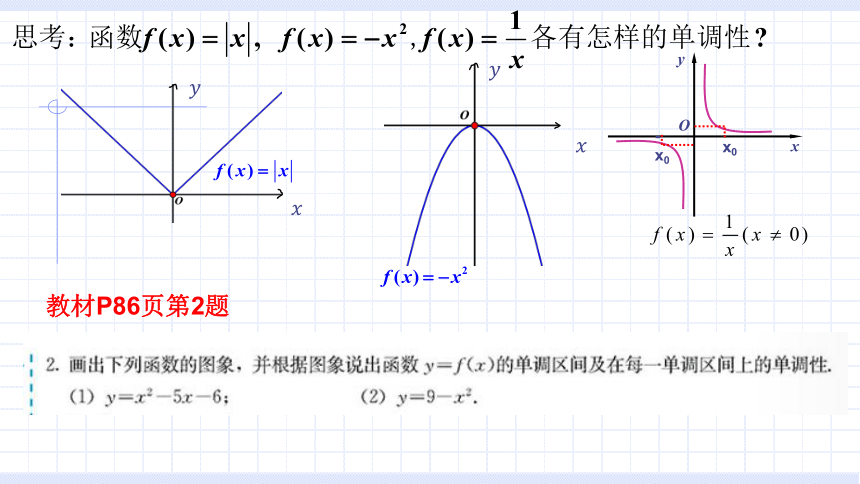
教材P86页第2题
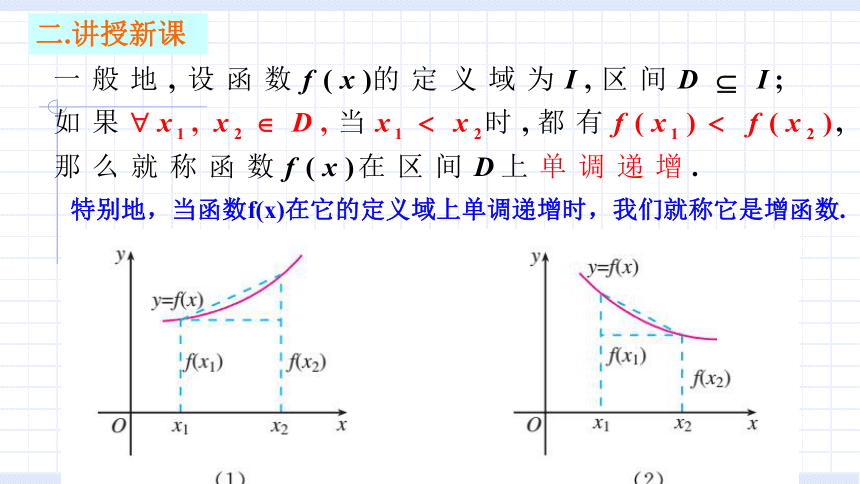
二.讲授新课
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
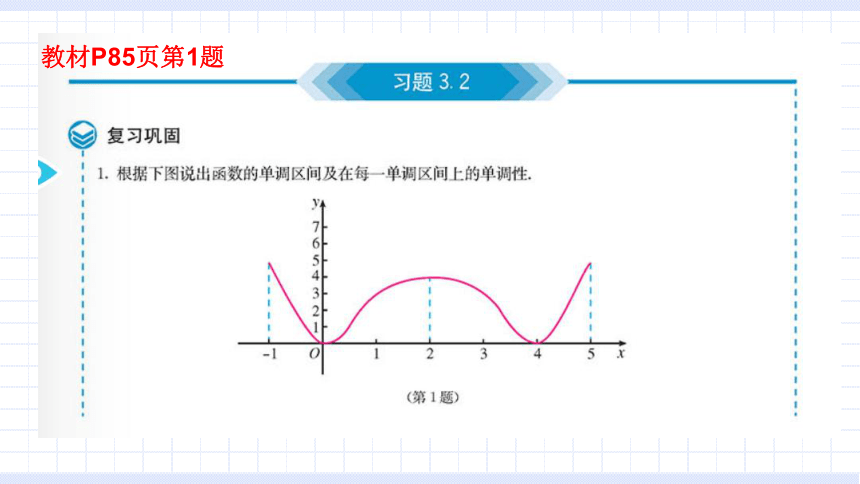
教材P85页第1题
教材P79练习2:根据定义证明函数
证明:
(取值)
(判号)
(下结论)
(作差)
(定义法)证明函数单调性的步骤
第一步:取值.即任取区间内的两个值,且x1第二步:作差(变形).将f(x1)-f(x2)通过因式分解、 配方、有理化等方法,向有利于判断差的符号的方向变形。
第三步:判号.确定差的符号,适当的时候需要进行讨论。
第四步:下结论.根据定义作出结论。
取值
作差(变形)
判号
下结论
教材P79练习3:
证明:
任取实数V1,V2∈(0,+∞)
且0∵p(V1)>0,p(V2)>0
>1
∴p(V1)>p(V2)
f(x)>0,则可以根据
大于或小于1
来比较f(x1)与f(x2)大小
又∵0三.针对性练习
1 、P32 课后练习 1 、2 、3 、 4
1.判断函数f(x)=x2+1在(0,+∞)上是增函数还是减函数?并给予证明。
2.证明:函数
1.判断函数f(x)=x2+1在(0,+∞)上是增函数还是减函数?并给予证明。
O
x
y
1
1
解:
函数f(x)=x2+1在(0,+∞)上是增函数.
下面给予证明:
设x1,x2∈(0,+∞),且x1<x2
∴函数f(x)=x2+1在(0,+∞)上是增函数.
增函数 减函数
图象
图象特征 从左至右,图象上升. 从左至右,图象下降.
数量
特征 y随x的增大而增大.当x1<x2时,y1<y2 y随x的增大而减小.当x1<x2时,y1>y2
O
x
y
x1
x2
y1
y2
O
x
y
x2
x1
y1
y2
四.小结:
注:1 、一定要掌握怎样用定义证明函数的单调性.
2、函数单调性是对于定义域内的某个子区间而言的。
(1)判断函数的单调性常用定义法和图象法,而证明函数的单调性则应严格按照单调性的定义操作.
取值
作差(变形)
判号
下结论
1、判断函数 在区间 (1,∞) 上的单调性并用单调性的定义证明。
2、求函数 在区间[2,9]上的最值。
3.2.1函数的最值
第二课时
函数最大值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.
讲授新课
(maximum value)
函数最大值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.
讲授新课
(maximum value)
函数最小值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≥M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最小值.
讲授新课
(minimum value)
烟花设计者就是按照这些数据设定引信的长度,以达到施放烟花的最佳效果.
于是,烟花冲出后1.5 s是它爆裂的最佳时刻,这时距地面的高度约为29 m.
P81练习3
已知函数f(x)=1/x,求函数在区间【2,6】上的最大值和最小值。
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
含参数二次函数的最值问题
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,1]上的最小值。
含参数二次函数的最值问题
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
含参数二次函数的最值问题
图象分析
【例2】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
含参数二次函数的最值问题
总结
求二次函数最值的类型及解法:
(1)二次函数在闭区间上的最值主要有三种类型:
定轴定区间、动轴定区间、定区间动轴
无论哪种类型,解决的关键是对称轴与区间的关系。当问题中含有参数时,要依据对称轴与区间的关系进行分类讨论;
(2)常结合二次函数在该区间上的单调性或图象求解,最值一般在区间的端点或顶点处取得。
方法总结
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
3.2.1函数的单调性
第一课时
观察图3.2-1中的各个函数图象,你能说说他们分别反映了相应函数的哪些性质吗?
请同学们观察这两个函数图象,指出这两个函数图象有什么特点?
二.引入新课
思考:如何利用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小” “随着x的增大,相应的f(x)也随着增大”?
y
x
O
x0
-x0
教材P86页第2题
二.讲授新课
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
教材P85页第1题
教材P79练习2:根据定义证明函数
证明:
(取值)
(判号)
(下结论)
(作差)
(定义法)证明函数单调性的步骤
第一步:取值.即任取区间内的两个值,且x1
第三步:判号.确定差的符号,适当的时候需要进行讨论。
第四步:下结论.根据定义作出结论。
取值
作差(变形)
判号
下结论
教材P79练习3:
证明:
任取实数V1,V2∈(0,+∞)
且0
>1
∴p(V1)>p(V2)
f(x)>0,则可以根据
大于或小于1
来比较f(x1)与f(x2)大小
又∵0
1 、P32 课后练习 1 、2 、3 、 4
1.判断函数f(x)=x2+1在(0,+∞)上是增函数还是减函数?并给予证明。
2.证明:函数
1.判断函数f(x)=x2+1在(0,+∞)上是增函数还是减函数?并给予证明。
O
x
y
1
1
解:
函数f(x)=x2+1在(0,+∞)上是增函数.
下面给予证明:
设x1,x2∈(0,+∞),且x1<x2
∴函数f(x)=x2+1在(0,+∞)上是增函数.
增函数 减函数
图象
图象特征 从左至右,图象上升. 从左至右,图象下降.
数量
特征 y随x的增大而增大.当x1<x2时,y1<y2 y随x的增大而减小.当x1<x2时,y1>y2
O
x
y
x1
x2
y1
y2
O
x
y
x2
x1
y1
y2
四.小结:
注:1 、一定要掌握怎样用定义证明函数的单调性.
2、函数单调性是对于定义域内的某个子区间而言的。
(1)判断函数的单调性常用定义法和图象法,而证明函数的单调性则应严格按照单调性的定义操作.
取值
作差(变形)
判号
下结论
1、判断函数 在区间 (1,∞) 上的单调性并用单调性的定义证明。
2、求函数 在区间[2,9]上的最值。
3.2.1函数的最值
第二课时
函数最大值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.
讲授新课
(maximum value)
函数最大值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.
讲授新课
(maximum value)
函数最小值概念:
一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≥M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最小值.
讲授新课
(minimum value)
烟花设计者就是按照这些数据设定引信的长度,以达到施放烟花的最佳效果.
于是,烟花冲出后1.5 s是它爆裂的最佳时刻,这时距地面的高度约为29 m.
P81练习3
已知函数f(x)=1/x,求函数在区间【2,6】上的最大值和最小值。
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
含参数二次函数的最值问题
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,1]上的最小值。
含参数二次函数的最值问题
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
含参数二次函数的最值问题
图象分析
【例2】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
含参数二次函数的最值问题
总结
求二次函数最值的类型及解法:
(1)二次函数在闭区间上的最值主要有三种类型:
定轴定区间、动轴定区间、定区间动轴
无论哪种类型,解决的关键是对称轴与区间的关系。当问题中含有参数时,要依据对称轴与区间的关系进行分类讨论;
(2)常结合二次函数在该区间上的单调性或图象求解,最值一般在区间的端点或顶点处取得。
方法总结
【例3】已知f(x)=x2+3x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的解析式,并求h(t)的最小值.
【例1】f(x)=x2+3x-5(0≤x≤6)的最小值 ;最大值 。
【例2】已知f(x)=x2+ax-5,求f(x)的在[0,2]上的最小值。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
