人教版(2019) 必修 第一册 第二章 匀变速直线运动的研究 单元测试(有解析)
文档属性
| 名称 | 人教版(2019) 必修 第一册 第二章 匀变速直线运动的研究 单元测试(有解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-29 15:59:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章 匀变速直线运动的研究单元测试
一、单选题
1.一物体做直线运动的v=t图象如图所示,关于物体的运动情况,下列说法正确的是( )
A. 在t=1s时,物体的运动方向改变 B. 在t=2s时,物体的加速度方向改变
C. 前5s内,物体路程为9m D. 前3s内,物体移动大小为5m
2.理想实验是科学研究中的一种重要方法,它把可靠事实和理论思维结合起来,可以深刻地揭示自然规律,以下实验中属于理想实验的是( )
A. 验证平行四边形定则 B. 伽利略的斜面实验
C. 用打点计时器测物体的加速度 D. 利用自由落体运动测定反应时间
3.如图所示是用照相机对一小球做自由落体运动频闪拍摄的照片,符合实际的是( )
A. B. C. D.
4.甲、乙两位同学进行百米赛跑,假如把他们的运动近似当作匀速直线运动来处理,他们同时从起跑线起跑,经过一段时间后他们的位置如图所示,在图中分别作出在这段时间内两人运动的位移s、速度v与时间t的关系图象,正确的是( )
A. B. C. D.
5.甲、乙两物体从同一位置出发且在同一直线上运动,它们的位移—时间(x-t)图象如图所示,由图象可知( )
A. 第3s末时,甲比乙的速度要小 B. 第4s末时,甲、乙间距离最大
C. 在0~4s内,甲、乙的平均速率相等 D. 在0~4s内,甲、乙的平均速度相等
6.匀变速直线运动是( )
①位移随时间均匀变化的直线运动
②速度随时间均匀变化的直线运动
③加速度随时间均匀变化的直线运动
④加速度的大小和方向恒定不变的直线运动.
A. ①② B. ②③ C. ②④ D. ③④
7.一枚火箭由地面竖直向上发射,其v-t图象如图所示,由图象可知( )
t2时刻火箭离地面最远
B. 在0~t2时间内火箭上升, t2~t3在时间内火箭下落
C. t3时刻火箭离地面最远
D. t3时刻火箭回到地面
8.伽利略在著名的斜面实验中,让小球分别沿倾角不同、阻力很小的斜面从静止开始滚下,他通过实验观察和逻辑推理,得到的正确结论有( )
A. 斜面长度一定时,小球从顶端滚到底端时的速度与倾角无关
B. 斜面长度一定时,小球从顶端滚到底端所需的时间与倾角无关
C. 倾角一定时,小球在斜面上的位移与时间成正比
D. 倾角一定时,小球在斜面上的速度与时间成正比
9.在变速直线运动中,下列关于速度,位移和加速度的说法中正确的是
A. 加速度越大,速度一定越大 B. 速度减小时,加速度也一定减小
C. 加速度减小时,速度可能增大 D. 速度减小时,位移也一定减小
二、多选题
10.甲、乙两车在平直公路上同向行驶,其v-t图像如图所示。已知两车在t=3s时并排行驶,则( )
A. 在t=1s时,甲车在乙车后
B. 在t=0时,甲车在乙车前7.5m
C. 两车另一次并排行驶的时刻是t=2s
D. 甲、乙两车两次并排行驶的位置之间沿公路方向的距离为40m
11.物体由静止做匀加速直线运动,第3s内通过的位移是10m,则( )
A. 第2s内的平均速度是10m/s B. 物体的加速度为4m/s2
C. 前3s内的位移是18m D. 3s末的速度是5.4m/s
12.如图所示,在水平地面同一位置的三个小球做斜上抛运动,沿三条不同的路径运动最终落在1、2、3三点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A. 落在1的小球抛出时的速率最大 B. 落在3的小球在空中运动时间最短
C. 三个小球运动时相同时间内速度变化相同 D. 三个小球运动到最高点时速度相等
13.甲、乙两车在一平直公路上同向行驶,其速度-时间图象如图所示,下列说法正确的是( )
乙车做曲线运动
内,乙车的位移大于甲车的位移
C. 时,两车一定不相遇
D. 内,必有某一时刻甲、乙两车的加速度相同
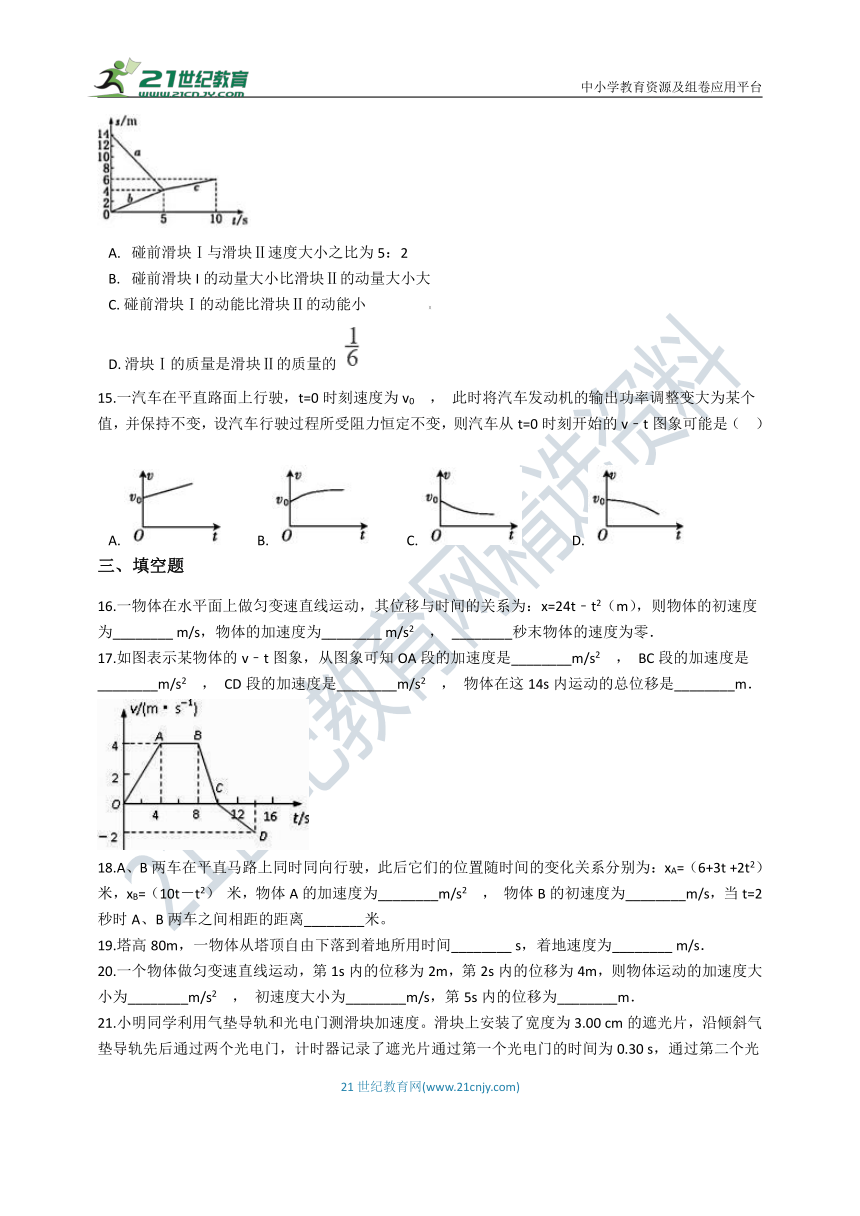
14.某研究小组通过实验测得两滑块碰撞前后运动的实验数据,得到如图所示的位移﹣时间图象。图中的线段a、b、c分别表示沿光滑水平面上同一条直线运动的滑块I、Ⅱ和它们发生正碰后结合体的位移变化关系。已知相互作用时间极短,由图象给出的信息可知( )
碰前滑块Ⅰ与滑块Ⅱ速度大小之比为5:2
碰前滑块I的动量大小比滑块Ⅱ的动量大小大
C. 碰前滑块Ⅰ的动能比滑块Ⅱ的动能小
D. 滑块Ⅰ的质量是滑块Ⅱ的质量的
15.一汽车在平直路面上行驶,t=0时刻速度为v0 , 此时将汽车发动机的输出功率调整变大为某个值,并保持不变,设汽车行驶过程所受阻力恒定不变,则汽车从t=0时刻开始的v﹣t图象可能是( )
A. B. C. D.
三、填空题
16.一物体在水平面上做匀变速直线运动,其位移与时间的关系为:x=24t﹣t2(m),则物体的初速度为________ m/s,物体的加速度为________ m/s2 , ________秒末物体的速度为零.
17.如图表示某物体的v﹣t图象,从图象可知OA段的加速度是________m/s2 , BC段的加速度是________m/s2 , CD段的加速度是________m/s2 , 物体在这14s内运动的总位移是________m.
18.A、B两车在平直马路上同时同向行驶,此后它们的位置随时间的变化关系分别为:xA=(6+3t +2t2) 米,xB=(10t-t2) 米,物体A的加速度为________m/s2 , 物体B的初速度为________m/s,当t=2秒时A、B两车之间相距的距离________米。
19.塔高80m,一物体从塔顶自由下落到着地所用时间________ s,着地速度为________ m/s.
20.一个物体做匀变速直线运动,第1s内的位移为2m,第2s内的位移为4m,则物体运动的加速度大小为________m/s2 , 初速度大小为________m/s,第5s内的位移为________m.
21.小明同学利用气垫导轨和光电门测滑块加速度。滑块上安装了宽度为3.00 cm的遮光片,沿倾斜气垫导轨先后通过两个光电门,计时器记录了遮光片通过第一个光电门的时间为0.30 s,通过第二个光电门的时间为0.10 s,小明用刻度尺测出两个光电门距离为20.00cm,则滑块的加速度为________
四、实验探究题
22.回答下列问题:
(1)打点计时器工作电源是________电源(填“直流”或“交流”),当电源的频率为50Hz时,每隔________秒打一个点
(2)研究匀变速直线运动规律实验装置如图1所示,右图给出了打点计时器打出的纸带,相邻的两个计数点的时间间隔为0.1s,相邻的两个计数点的距离如图2所示:(本题所有结果保留两位小数)
① 分析纸带,可求得打计数点1、3时小车对应的速度分别为:v1=________m/s;v3=________m/s.
②根据纸带数据,可求出小车的加速度为a=________m/s2 .
五、综合题
23.某物理实验小组在游泳池做了一个实验:将一个小木球离水面5m高静止释放(不计空气阻力),经1.50s后落入池底速度刚好为零.假定木球在水中做匀减速运动,重力加速度g=10m/s2 . 求:
(1)木球做自由落体运动的时间;
(2)木球入水时的速度大小;
(3)木球在水中运动的加速度的大小及游泳池水的深度.
24.如图所示,方形木箱质量为M,其内用两轻绳将一质量m=1.0kg的小球悬挂于P、Q两点,两细绳与水平的车顶面的夹角分别为60°和30°.水平传送带AB长l=30m,以v=15m/s的速度顺时针转动,木箱与传送带间动摩擦因数 =0.75,(g=10m/s2)求:
(1)设木箱为质点,且木箱由静止放到传送带上,那么经过多长时间木箱能够从A运动到传送带的另一端B处;
(2)木箱放到传送带上A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为多少?
答案
一、单选题
1.【答案】C
【解析】【解答】解:A、0﹣2s内速度都为正,方向不变,故A错误;
B、图线斜率表示加速度,根据图象可知,2s前后一小段时间内,斜率不变,加速度不变,方向没有改变,故B错误;
C、速度时间图线与时间轴围成的面积表示位移,则前5s内,物体路程s= .故C正确;
D、速度时间图线与时间轴围成的面积表示位移,前3s内,物体移动大小为x= ,故D错误;
故选:C
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,通过这些性质分析即可。
2.【答案】 B
【解析】【解答】解:A、验证平行四边形定则采用的是“等效替代”的思想,故A错误;
B、伽利略的斜面实验,抓住主要因素,忽略了次要因素,从而更深刻地反映了自然规律,属于理想实验,故B正确;
C、用打点计时器测物体的加速度是在实验室进行是实际实验,故C错误;
D、利用自由落体运动测定反应时间是实际进行的实验,不是理想实验,故D错误.
故选B.
【分析】伽利略的理想实验,以可靠的事实为基础,经过抽象思维,抓住主要因素,忽略了次要因素,从而更深刻地反映了自然规律.这种把可靠的事实和深刻的理论思维结合起来的理想实验,是科学研究中的一种重要方法.
3.【答案】 D
【解析】【解答】小球做自由落体,在第1T、第2T、第3T的位移之比为1:3:5。
A.间距越来越小,是减速运动。A不符合题意。
B.间距先变小后变大,先减速后加速。B不符合题意。
C.间距不变,是匀速运动。C不符合题意。
D.间距逐渐变大,是加速运动。D符合题意。
故答案为:D
【分析】利用位移公式可以判别相邻位移之比;利用自由落体的速度及位移可以判别对应的照片。
4.【答案】 B
【解析】【解答】解:由题意知甲乙两人都做匀速直线运动,甲与乙的速度保持不变,在相等时间t内S甲<S乙 , 甲的速度小于乙的速度.符合条件的图象是B.
故选B.
【分析】两人都做匀速直线运动,他们的路程随时间均匀增加,S﹣t图象是一条倾斜的直线;他们的速度v保持不变,v﹣t图象时一条平行于时间轴的直线;由图知在相等时间t内,甲的路程S甲小于乙的路程S乙 , 即S甲<S乙 , 由v= 知甲的速度小于乙的速度.
5.【答案】 D
【解析】【解答】A.由于位移-时间图象的斜率的速度,可以从图中可得 , ,正负表示速度的方向,所以甲比乙的速度要大,故A错误;
B.4s秒末两物体的位置坐标相同,说明两物体相遇,故B错误;
C.乙物体的速度(斜率)始终为正值,即速度始终为正方向,甲物体前两秒内速度为正方向,2秒末到4秒末速度为负方向,又4s秒末两物体的位置坐标相同,所以4s内甲的路程大于乙的路程,所用时间相等,所以甲的平均速率大于乙的平均速率,故C错误;
D.由图知4s内甲的位移大小为 ,乙的位移大小为 ,位移相等,所用时间也相等,则由平均速度公式 知,平均速度相等,故D正确;
故选D。
【分析】利用斜率可以比较速度的大小;利用位置坐标可以判别距离;利用位移与时间的比值可以比较平均速度。
6.【答案】 C
【解析】【解答】解:根据x= 知,位移不是随时间均匀变化,根据v=v0+at知,速度随时间均匀变化,匀变速直线运动的加速度保持不变,故②④正确.
故选:C.
【分析】匀变速直线运动的加速度保持不变,速度随时间均匀变化.
7.【答案】 C
【解析】【解答】A、由图象上部面积代表的位移为正,下部面积代表的位移为负,可知由 到 位移一直在增大,故 不是最高点, 才是最高点,AD不符合题意;C符合题意;
B、速度的正负表示方向,故可 段和 段方向是一样的,故都是上升的,B不符合题意。
故答案为:C
【分析】利用面积可以找出距离地面最远的时刻,由于速度只有一个方向所以火箭只是向上运动;面积最大离地面最远。
8.【答案】D
【解析】【解答】解:A、若斜面光滑,小球从顶端滚到底端时的速度大小的确与倾角无关;但由于实际斜面有摩擦,故伽利略并没有能够用实验证明这一点;故A错误; B、斜面长度一定时,小球从顶端滚到底端所需的时间随倾角的增大而减小,故B错误;
C、伽利略通过实验测定出小球沿斜面下滑的运动是匀加速直线运动,位移与时间的二次方成正比,并证明了速度与时间成正比,故C错误,D正确;
故选:D.
【分析】伽利略通过实验观察和逻辑推理发现,小球沿斜面滚下的运动的确是匀加速直线运动,换用不同的质量的小球,从不同高度开始滚动,只要斜面的倾角一定,小球的加速度都是相同的;不断增大斜面的倾角,重复上述实验,得知小球的加速度随斜面倾角的增大而增大.
9.【答案】 C
【解析】【分析】加速度表示速度的变化快慢,与速度、速度变化量的大小无关,C对;如果物体做减速运动,虽然速度减小,但位移是增大的,D错;故选C
【点评】本题难度较小,明确加速度的概念,加速度大小表示速度的变化快慢,与速度、速度变化量都没有关系
二、多选题
10.【答案】 B,D
【解析】【解答】AC.根据速度时间图象的“面积”表示位移,由几何知识可知,1-3s甲、乙两车通过的位移相等,两车在t=3s时并排行驶,所以两车在t=1s时也并排行驶,AC不符合题意;
B.由图象可知,0-1s内乙车比甲车多走的距离为
而t=1s时刻两车并排而行,可知在t=0时,甲车在乙车前7.5m,B符合题意;
D.由图像可知,甲、乙两车两次并排行驶的位置之间沿公路方向的距离等于从t=1s到t=3s过程中甲车的位移,则为 ,
D符合题意。
故答案为:BD
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,两图像的交点意味着两个物体具有相同的速度,结合选项分析即可。
11.【答案】 B,C
【解析】【解答】A、根据匀变速直线运动的推论平均速度等于中间时刻的瞬时速度,有 ;A不符合题意.
B、设加速度为a,则 ,可得: ;B符合题意.
C、前3s内的位移为 ;C符合题意.
D、3s末的速度为v=at=4×3=12m/s,则D不符合题意.
故答案为:BC.
【分析】利用平均速度公式可以求出平均速度的大小;利用位移公式可以求出加速度的大小;利用位移公式可以求出位移的大小;利用速度公式可以求出速度的大小。
12.【答案】 A,C
【解析】【解答】解:设任一小球初速度大小为v0 , 初速度的竖直分量为vy , 水平分量为vx , 初速度与水平方向的夹角为α,上升的最大高度为h,运动时间为t,落地速度大小为v.
A、C、D、取竖直向上方向为正方向,小球竖直方向上做匀减速直线运动,加速度为a=﹣g,由0﹣vy2=﹣2gh,得:
vy= ,h相同,vy相同,则三个小球初速度的竖直分量相同.
由速度的分解知:vy=v0sinα,由于α不同,所以v0不同,沿路径1抛出时的小球的初速度最大.
根据机械能守恒定律得知,小球落地时与抛出时速率相等,所以可知三个小球落地时的速率不等,也是沿路径1抛出时的小球的初速度最大.
又有 vy=vxtanα,vy相同,α不同,则vx不同,初速度水平分量不等;只有竖直方向速度发生变化,而初速度均相同,故速度变化量均相同;故A正确,C正确,D错误.
B、由运动学公式有:h= g( )2 , 则得:t=2 ,则知三个球运动的时间相等;故B错误.
故选:AC.
【分析】三个小球都做斜抛运动,运用运动的分解法,将其运动分解为竖直和水平两个方向研究,水平方向做匀速直线运动,竖直方向做竖直上抛运动,根据运动学公式列式,再进行分析.
13.【答案】 B,D
【解析】【解答】A.速度-时间图象只能表示直线运动的规律,不是物体运动的轨迹,可知乙车做直线运动,A不符合题意。
B.根据速度时间图象与时间轴所围的“面积”大小表示位移,由图象可知,0-10s内,乙车的位移大于甲车的位移,B符合题意。
C.由于t=0时刻两车的位置关系未知,则t=10s时,两车可能相遇,C不符合题意。
D.v-t图象的斜率表示加速度,则知0-10s内,乙车的加速度逐渐减小,先大于甲车的加速度,后小于甲车的加速度,则必有某一时刻甲乙两车的加速度相同,D符合题意。
故答案为:BD
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,两图像的交点意味着两个物体具有相同的速度,结合选项分析即可。
14.【答案】 A,D
【解析】【解答】解:A、根据s﹣t图象的斜率等于速度,则得:碰撞前滑块I速度为:v1= m/s=﹣2m/s,大小为2m/s;滑块Ⅱ速度为v2= m/s=0.8m/s,则碰前速度之比为5:2,A符合题意;
B、碰撞前后系统动量守恒,碰撞前,滑块I速度为负,动量为负,滑块Ⅱ的速度为正,动量为负。由于碰撞后动量为正,故碰撞前总动量也为正,故碰撞前滑块I的动量比滑块Ⅱ小,B不符合题意;
D、根据动量守恒定律,有:m1v1+m2v2=(m1+m2)v
代入数据,有:﹣2m1+0.8m2=0.4(m1+m2),联立解得:m2=6m1 , D符合题意;
C、碰前滑块Ⅰ的动能与滑块Ⅱ的动能之比为 ,所以碰前滑块Ⅰ比滑块Ⅱ的动能大,C不符合题意;
故答案为:AD
【分析】s-t图像中,横坐标为时间,纵坐标为位移,图像的斜率是速度,通过这些性质结合选项分析即可。
15.【答案】 B,C
【解析】【解答】解:汽车匀速运动,牵引力等于阻力,此时P=Fv0=fv0 , 若在t=0时刻将汽车发动机的输出功率调为另一个恒定值,且这个定值比P小,则瞬间牵引力减小,牵引力小于阻力,根据牛顿第二定律可知a= ,则加速度反向减小,故汽车做加速度减小的减速运动,
若在t=0时刻将汽车发动机的输出功率调为另一个恒定值,且这个定值比P大,则根据P=Fv可知瞬间牵引力增大,随着速度增大,牵引力减小,根据牛顿第二定律可知a= ,则加速度减小,故汽车做加速度减小的加速运动,故BC正确,AD错误.
故选:BC.
【分析】本题要分功率变大和变小两种情况,根据P=Fv以及牛顿第二定律分析速度和加速度的变化情况,从而选择图象.
三、填空题
16.【答案】24;﹣2;12
【解析】【解答】解:解:由x=v0t+ at2=24t﹣t2 , 得初速度v0=24m/s,加速度a=﹣2m/s2 .
当物体的速度为0时,由v=v0+at得:
故答案为:24,﹣2,12.
【分析】根据匀变速直线运动的位移时间公式x=v0t+ at2得出质点的初速度和加速度.由速度公式即可求出物体速度为0的时间.
17.【答案】1;﹣2;﹣0.5;24
【解析】【解答】OA段的加速度 ;
BC段的加速度 ;
CD段的加速度 ;
物体在14s内的总位移为图象与时间轴围成的面积,故位移为: ×(4+10)×4- ×4×2=24m;
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,通过这些性质分析即可。
18.【答案】 4;10;4
【解析】【解答】根据匀变速直线运动的公式:
对比:
xA=6+3t +2t2
可得A的加速度为4m/s2
同理对比:xB=10t-t2
可得物体B的初速度为10m/s.当t=2s时,A的位置为xA=20m;B的位置为:xB=16m,所以AB相距为:
【分析】结合题目中给出的物体位移与时间的关系,对比匀变速直线运动公式,求出物体的初速度和加速度,再结合选项分析求解即可。
19.【答案】4;40
【解析】【解答】解:物体自由落体运动,根据位移时间关系公式 有:h= ;
物体自由落体运动,根据速度时间关系公式,着地速度为:v=gt=10×4=40m/s;
故答案为:4,40
【分析】自由落体运动是初速度为零的匀加速直线运动,初速度为零的匀加速直线运动,由h= 即可求出运动的时间,由v=gt即可求出末速度.
20.【答案】2;1;10
【解析】【解答】根据位移公式 ,可得:
第1s内的位移: ①
第2s内的位移: ②
联立两式,可得:v0=1m/s a=2m/s2
第5s内的位移:
故答案为:2,1,10.
【分析】根据位移公式 ,物体第2s内的位移等于前2s内的位移减去第1s内的位移,联立列式可求解
21.【答案】 0.2m/s2
【解析】【解答】遮光板通过第一个光电门的速度 ,遮光板通过第二个光电门的速度 ,则加速度 .
【分析】当运动位移很短时,物体的平均速度等于物体运动的瞬时速度,利用宽度除以挡光的时间即可;结合物体的初末速度,利用加速度定义式求解即可。
四、实验探究题
22.【答案】 (1)交流;0.02
(2)0.36;0.43;0.35
【解析】解:(1)电磁打点计时器的电源应是交流电源,实验室使用我国民用电时,每隔0.02s打一次点,
如果每打5个取一个计数点,即相邻两个计数点间的时间间隔为0.1s.(2)①根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上1点时小车的瞬时速度大小.
v1= m/s=0.36m/s
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上3点时小车的瞬时速度大小.
v3= m/s=0.43m/s②根据加速度定义式得
a= = =0.35m/s2 . 故答案为:(1)交流,0.02;(2)①0.36;0.43;②0.35.
【分析】(1)根据打点计时器的原理结合周期公式,求解。
(2)纸带点分析过程中,中间时刻的瞬时速度等于全程的平均速度,相邻相等时间间隔位移之差恒定。
五、综合题
23.【答案】 (1)解:设木球做自由落体运动的时间为t1 ,
由运动学公式得:h= gt12 ,
解得:t1= = =1s
答:木球做自由落体运动的时间为1s
(2)解:木球入水时的速度:v=gt1=10×1=10m/s
答:木球入水时的速度大小为10m/s
(3)解:木球在水中运动的时间:t2=t﹣t1=1.5﹣1=0.5s,
木球做匀减速运动过程的加速度大小:a= = =20m/s2 ,
游泳池水的深度:h′= t2= ×0.5=2.5m
答:木球在水中运动的加速度的大小为20m/s2 , 游泳池水的深度为2.5m.
【解析】【分析】(1)应用匀变速直线运动的位移公式可以求出自由下落的时间.(2)应用匀变速直线运动的速度公式可以求出木球入水时的速度.(3)应用加速度的定义式可以求出木球在水中的加速度,应用平均速度公式可以求出水的深度.
24.【答案】 (1)解:木箱由静止放到传送带上,开始过程,根据牛顿第二定律得
对木箱:μMg=Ma
a=μg=0.75×10m/s2=7.5m/s2
木箱加速位移: =15m
木箱加速时间: =2s
x1=15m<l=30m 所以还要在传送带上匀速后一段距离
木箱匀速时运动的时间:l﹣x1=vt2
t2= =1s
所以木箱从A运动到传送带另一端B处经历时间t=t1+t2=3s
答:木箱由静止放到传送带上,经过3s时间木箱能够从A运动到传送带的另一端B处
(2)解:设绳P伸直恰好无拉力时木箱的加速度为a0 , 则由牛顿第二定律得
mgtan30°=ma0
代入解得: <7.5m/s2
故小球已经飘起来,绳P的张力大小TP=0
此时有:
代入解得TQ=1.25N
答:木箱放到传送带A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为0和1.25N
【解析】【分析】(1)木箱由静止放到传送带上,水平方向先做受到滑动摩擦力,做匀加速直线运动,由牛顿第二定律求出加速度,由速度公式求出木箱速度与传送带相同时经历的时间和通过的位移,并判断木箱是否有匀速运动过程.如有,求出时间,再求总时间.(2)由牛顿第二定律求出绳P恰好张力时木箱的加速度a0 , 根据a0与木箱加速过程的加速度a的大小比较,判断绳P是否有张力,再由牛顿第二定律求解两绳的张力.
21世纪教育网(www.21cnjy.com)
第二章 匀变速直线运动的研究单元测试
一、单选题
1.一物体做直线运动的v=t图象如图所示,关于物体的运动情况,下列说法正确的是( )
A. 在t=1s时,物体的运动方向改变 B. 在t=2s时,物体的加速度方向改变
C. 前5s内,物体路程为9m D. 前3s内,物体移动大小为5m
2.理想实验是科学研究中的一种重要方法,它把可靠事实和理论思维结合起来,可以深刻地揭示自然规律,以下实验中属于理想实验的是( )
A. 验证平行四边形定则 B. 伽利略的斜面实验
C. 用打点计时器测物体的加速度 D. 利用自由落体运动测定反应时间
3.如图所示是用照相机对一小球做自由落体运动频闪拍摄的照片,符合实际的是( )
A. B. C. D.
4.甲、乙两位同学进行百米赛跑,假如把他们的运动近似当作匀速直线运动来处理,他们同时从起跑线起跑,经过一段时间后他们的位置如图所示,在图中分别作出在这段时间内两人运动的位移s、速度v与时间t的关系图象,正确的是( )
A. B. C. D.
5.甲、乙两物体从同一位置出发且在同一直线上运动,它们的位移—时间(x-t)图象如图所示,由图象可知( )
A. 第3s末时,甲比乙的速度要小 B. 第4s末时,甲、乙间距离最大
C. 在0~4s内,甲、乙的平均速率相等 D. 在0~4s内,甲、乙的平均速度相等
6.匀变速直线运动是( )
①位移随时间均匀变化的直线运动
②速度随时间均匀变化的直线运动
③加速度随时间均匀变化的直线运动
④加速度的大小和方向恒定不变的直线运动.
A. ①② B. ②③ C. ②④ D. ③④
7.一枚火箭由地面竖直向上发射,其v-t图象如图所示,由图象可知( )
t2时刻火箭离地面最远
B. 在0~t2时间内火箭上升, t2~t3在时间内火箭下落
C. t3时刻火箭离地面最远
D. t3时刻火箭回到地面
8.伽利略在著名的斜面实验中,让小球分别沿倾角不同、阻力很小的斜面从静止开始滚下,他通过实验观察和逻辑推理,得到的正确结论有( )
A. 斜面长度一定时,小球从顶端滚到底端时的速度与倾角无关
B. 斜面长度一定时,小球从顶端滚到底端所需的时间与倾角无关
C. 倾角一定时,小球在斜面上的位移与时间成正比
D. 倾角一定时,小球在斜面上的速度与时间成正比
9.在变速直线运动中,下列关于速度,位移和加速度的说法中正确的是
A. 加速度越大,速度一定越大 B. 速度减小时,加速度也一定减小
C. 加速度减小时,速度可能增大 D. 速度减小时,位移也一定减小
二、多选题
10.甲、乙两车在平直公路上同向行驶,其v-t图像如图所示。已知两车在t=3s时并排行驶,则( )
A. 在t=1s时,甲车在乙车后
B. 在t=0时,甲车在乙车前7.5m
C. 两车另一次并排行驶的时刻是t=2s
D. 甲、乙两车两次并排行驶的位置之间沿公路方向的距离为40m
11.物体由静止做匀加速直线运动,第3s内通过的位移是10m,则( )
A. 第2s内的平均速度是10m/s B. 物体的加速度为4m/s2
C. 前3s内的位移是18m D. 3s末的速度是5.4m/s
12.如图所示,在水平地面同一位置的三个小球做斜上抛运动,沿三条不同的路径运动最终落在1、2、3三点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A. 落在1的小球抛出时的速率最大 B. 落在3的小球在空中运动时间最短
C. 三个小球运动时相同时间内速度变化相同 D. 三个小球运动到最高点时速度相等
13.甲、乙两车在一平直公路上同向行驶,其速度-时间图象如图所示,下列说法正确的是( )
乙车做曲线运动
内,乙车的位移大于甲车的位移
C. 时,两车一定不相遇
D. 内,必有某一时刻甲、乙两车的加速度相同
14.某研究小组通过实验测得两滑块碰撞前后运动的实验数据,得到如图所示的位移﹣时间图象。图中的线段a、b、c分别表示沿光滑水平面上同一条直线运动的滑块I、Ⅱ和它们发生正碰后结合体的位移变化关系。已知相互作用时间极短,由图象给出的信息可知( )
碰前滑块Ⅰ与滑块Ⅱ速度大小之比为5:2
碰前滑块I的动量大小比滑块Ⅱ的动量大小大
C. 碰前滑块Ⅰ的动能比滑块Ⅱ的动能小
D. 滑块Ⅰ的质量是滑块Ⅱ的质量的
15.一汽车在平直路面上行驶,t=0时刻速度为v0 , 此时将汽车发动机的输出功率调整变大为某个值,并保持不变,设汽车行驶过程所受阻力恒定不变,则汽车从t=0时刻开始的v﹣t图象可能是( )
A. B. C. D.
三、填空题
16.一物体在水平面上做匀变速直线运动,其位移与时间的关系为:x=24t﹣t2(m),则物体的初速度为________ m/s,物体的加速度为________ m/s2 , ________秒末物体的速度为零.
17.如图表示某物体的v﹣t图象,从图象可知OA段的加速度是________m/s2 , BC段的加速度是________m/s2 , CD段的加速度是________m/s2 , 物体在这14s内运动的总位移是________m.
18.A、B两车在平直马路上同时同向行驶,此后它们的位置随时间的变化关系分别为:xA=(6+3t +2t2) 米,xB=(10t-t2) 米,物体A的加速度为________m/s2 , 物体B的初速度为________m/s,当t=2秒时A、B两车之间相距的距离________米。
19.塔高80m,一物体从塔顶自由下落到着地所用时间________ s,着地速度为________ m/s.
20.一个物体做匀变速直线运动,第1s内的位移为2m,第2s内的位移为4m,则物体运动的加速度大小为________m/s2 , 初速度大小为________m/s,第5s内的位移为________m.
21.小明同学利用气垫导轨和光电门测滑块加速度。滑块上安装了宽度为3.00 cm的遮光片,沿倾斜气垫导轨先后通过两个光电门,计时器记录了遮光片通过第一个光电门的时间为0.30 s,通过第二个光电门的时间为0.10 s,小明用刻度尺测出两个光电门距离为20.00cm,则滑块的加速度为________
四、实验探究题
22.回答下列问题:
(1)打点计时器工作电源是________电源(填“直流”或“交流”),当电源的频率为50Hz时,每隔________秒打一个点
(2)研究匀变速直线运动规律实验装置如图1所示,右图给出了打点计时器打出的纸带,相邻的两个计数点的时间间隔为0.1s,相邻的两个计数点的距离如图2所示:(本题所有结果保留两位小数)
① 分析纸带,可求得打计数点1、3时小车对应的速度分别为:v1=________m/s;v3=________m/s.
②根据纸带数据,可求出小车的加速度为a=________m/s2 .
五、综合题
23.某物理实验小组在游泳池做了一个实验:将一个小木球离水面5m高静止释放(不计空气阻力),经1.50s后落入池底速度刚好为零.假定木球在水中做匀减速运动,重力加速度g=10m/s2 . 求:
(1)木球做自由落体运动的时间;
(2)木球入水时的速度大小;
(3)木球在水中运动的加速度的大小及游泳池水的深度.
24.如图所示,方形木箱质量为M,其内用两轻绳将一质量m=1.0kg的小球悬挂于P、Q两点,两细绳与水平的车顶面的夹角分别为60°和30°.水平传送带AB长l=30m,以v=15m/s的速度顺时针转动,木箱与传送带间动摩擦因数 =0.75,(g=10m/s2)求:
(1)设木箱为质点,且木箱由静止放到传送带上,那么经过多长时间木箱能够从A运动到传送带的另一端B处;
(2)木箱放到传送带上A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为多少?
答案
一、单选题
1.【答案】C
【解析】【解答】解:A、0﹣2s内速度都为正,方向不变,故A错误;
B、图线斜率表示加速度,根据图象可知,2s前后一小段时间内,斜率不变,加速度不变,方向没有改变,故B错误;
C、速度时间图线与时间轴围成的面积表示位移,则前5s内,物体路程s= .故C正确;
D、速度时间图线与时间轴围成的面积表示位移,前3s内,物体移动大小为x= ,故D错误;
故选:C
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,通过这些性质分析即可。
2.【答案】 B
【解析】【解答】解:A、验证平行四边形定则采用的是“等效替代”的思想,故A错误;
B、伽利略的斜面实验,抓住主要因素,忽略了次要因素,从而更深刻地反映了自然规律,属于理想实验,故B正确;
C、用打点计时器测物体的加速度是在实验室进行是实际实验,故C错误;
D、利用自由落体运动测定反应时间是实际进行的实验,不是理想实验,故D错误.
故选B.
【分析】伽利略的理想实验,以可靠的事实为基础,经过抽象思维,抓住主要因素,忽略了次要因素,从而更深刻地反映了自然规律.这种把可靠的事实和深刻的理论思维结合起来的理想实验,是科学研究中的一种重要方法.
3.【答案】 D
【解析】【解答】小球做自由落体,在第1T、第2T、第3T的位移之比为1:3:5。
A.间距越来越小,是减速运动。A不符合题意。
B.间距先变小后变大,先减速后加速。B不符合题意。
C.间距不变,是匀速运动。C不符合题意。
D.间距逐渐变大,是加速运动。D符合题意。
故答案为:D
【分析】利用位移公式可以判别相邻位移之比;利用自由落体的速度及位移可以判别对应的照片。
4.【答案】 B
【解析】【解答】解:由题意知甲乙两人都做匀速直线运动,甲与乙的速度保持不变,在相等时间t内S甲<S乙 , 甲的速度小于乙的速度.符合条件的图象是B.
故选B.
【分析】两人都做匀速直线运动,他们的路程随时间均匀增加,S﹣t图象是一条倾斜的直线;他们的速度v保持不变,v﹣t图象时一条平行于时间轴的直线;由图知在相等时间t内,甲的路程S甲小于乙的路程S乙 , 即S甲<S乙 , 由v= 知甲的速度小于乙的速度.
5.【答案】 D
【解析】【解答】A.由于位移-时间图象的斜率的速度,可以从图中可得 , ,正负表示速度的方向,所以甲比乙的速度要大,故A错误;
B.4s秒末两物体的位置坐标相同,说明两物体相遇,故B错误;
C.乙物体的速度(斜率)始终为正值,即速度始终为正方向,甲物体前两秒内速度为正方向,2秒末到4秒末速度为负方向,又4s秒末两物体的位置坐标相同,所以4s内甲的路程大于乙的路程,所用时间相等,所以甲的平均速率大于乙的平均速率,故C错误;
D.由图知4s内甲的位移大小为 ,乙的位移大小为 ,位移相等,所用时间也相等,则由平均速度公式 知,平均速度相等,故D正确;
故选D。
【分析】利用斜率可以比较速度的大小;利用位置坐标可以判别距离;利用位移与时间的比值可以比较平均速度。
6.【答案】 C
【解析】【解答】解:根据x= 知,位移不是随时间均匀变化,根据v=v0+at知,速度随时间均匀变化,匀变速直线运动的加速度保持不变,故②④正确.
故选:C.
【分析】匀变速直线运动的加速度保持不变,速度随时间均匀变化.
7.【答案】 C
【解析】【解答】A、由图象上部面积代表的位移为正,下部面积代表的位移为负,可知由 到 位移一直在增大,故 不是最高点, 才是最高点,AD不符合题意;C符合题意;
B、速度的正负表示方向,故可 段和 段方向是一样的,故都是上升的,B不符合题意。
故答案为:C
【分析】利用面积可以找出距离地面最远的时刻,由于速度只有一个方向所以火箭只是向上运动;面积最大离地面最远。
8.【答案】D
【解析】【解答】解:A、若斜面光滑,小球从顶端滚到底端时的速度大小的确与倾角无关;但由于实际斜面有摩擦,故伽利略并没有能够用实验证明这一点;故A错误; B、斜面长度一定时,小球从顶端滚到底端所需的时间随倾角的增大而减小,故B错误;
C、伽利略通过实验测定出小球沿斜面下滑的运动是匀加速直线运动,位移与时间的二次方成正比,并证明了速度与时间成正比,故C错误,D正确;
故选:D.
【分析】伽利略通过实验观察和逻辑推理发现,小球沿斜面滚下的运动的确是匀加速直线运动,换用不同的质量的小球,从不同高度开始滚动,只要斜面的倾角一定,小球的加速度都是相同的;不断增大斜面的倾角,重复上述实验,得知小球的加速度随斜面倾角的增大而增大.
9.【答案】 C
【解析】【分析】加速度表示速度的变化快慢,与速度、速度变化量的大小无关,C对;如果物体做减速运动,虽然速度减小,但位移是增大的,D错;故选C
【点评】本题难度较小,明确加速度的概念,加速度大小表示速度的变化快慢,与速度、速度变化量都没有关系
二、多选题
10.【答案】 B,D
【解析】【解答】AC.根据速度时间图象的“面积”表示位移,由几何知识可知,1-3s甲、乙两车通过的位移相等,两车在t=3s时并排行驶,所以两车在t=1s时也并排行驶,AC不符合题意;
B.由图象可知,0-1s内乙车比甲车多走的距离为
而t=1s时刻两车并排而行,可知在t=0时,甲车在乙车前7.5m,B符合题意;
D.由图像可知,甲、乙两车两次并排行驶的位置之间沿公路方向的距离等于从t=1s到t=3s过程中甲车的位移,则为 ,
D符合题意。
故答案为:BD
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,两图像的交点意味着两个物体具有相同的速度,结合选项分析即可。
11.【答案】 B,C
【解析】【解答】A、根据匀变速直线运动的推论平均速度等于中间时刻的瞬时速度,有 ;A不符合题意.
B、设加速度为a,则 ,可得: ;B符合题意.
C、前3s内的位移为 ;C符合题意.
D、3s末的速度为v=at=4×3=12m/s,则D不符合题意.
故答案为:BC.
【分析】利用平均速度公式可以求出平均速度的大小;利用位移公式可以求出加速度的大小;利用位移公式可以求出位移的大小;利用速度公式可以求出速度的大小。
12.【答案】 A,C
【解析】【解答】解:设任一小球初速度大小为v0 , 初速度的竖直分量为vy , 水平分量为vx , 初速度与水平方向的夹角为α,上升的最大高度为h,运动时间为t,落地速度大小为v.
A、C、D、取竖直向上方向为正方向,小球竖直方向上做匀减速直线运动,加速度为a=﹣g,由0﹣vy2=﹣2gh,得:
vy= ,h相同,vy相同,则三个小球初速度的竖直分量相同.
由速度的分解知:vy=v0sinα,由于α不同,所以v0不同,沿路径1抛出时的小球的初速度最大.
根据机械能守恒定律得知,小球落地时与抛出时速率相等,所以可知三个小球落地时的速率不等,也是沿路径1抛出时的小球的初速度最大.
又有 vy=vxtanα,vy相同,α不同,则vx不同,初速度水平分量不等;只有竖直方向速度发生变化,而初速度均相同,故速度变化量均相同;故A正确,C正确,D错误.
B、由运动学公式有:h= g( )2 , 则得:t=2 ,则知三个球运动的时间相等;故B错误.
故选:AC.
【分析】三个小球都做斜抛运动,运用运动的分解法,将其运动分解为竖直和水平两个方向研究,水平方向做匀速直线运动,竖直方向做竖直上抛运动,根据运动学公式列式,再进行分析.
13.【答案】 B,D
【解析】【解答】A.速度-时间图象只能表示直线运动的规律,不是物体运动的轨迹,可知乙车做直线运动,A不符合题意。
B.根据速度时间图象与时间轴所围的“面积”大小表示位移,由图象可知,0-10s内,乙车的位移大于甲车的位移,B符合题意。
C.由于t=0时刻两车的位置关系未知,则t=10s时,两车可能相遇,C不符合题意。
D.v-t图象的斜率表示加速度,则知0-10s内,乙车的加速度逐渐减小,先大于甲车的加速度,后小于甲车的加速度,则必有某一时刻甲乙两车的加速度相同,D符合题意。
故答案为:BD
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,两图像的交点意味着两个物体具有相同的速度,结合选项分析即可。
14.【答案】 A,D
【解析】【解答】解:A、根据s﹣t图象的斜率等于速度,则得:碰撞前滑块I速度为:v1= m/s=﹣2m/s,大小为2m/s;滑块Ⅱ速度为v2= m/s=0.8m/s,则碰前速度之比为5:2,A符合题意;
B、碰撞前后系统动量守恒,碰撞前,滑块I速度为负,动量为负,滑块Ⅱ的速度为正,动量为负。由于碰撞后动量为正,故碰撞前总动量也为正,故碰撞前滑块I的动量比滑块Ⅱ小,B不符合题意;
D、根据动量守恒定律,有:m1v1+m2v2=(m1+m2)v
代入数据,有:﹣2m1+0.8m2=0.4(m1+m2),联立解得:m2=6m1 , D符合题意;
C、碰前滑块Ⅰ的动能与滑块Ⅱ的动能之比为 ,所以碰前滑块Ⅰ比滑块Ⅱ的动能大,C不符合题意;
故答案为:AD
【分析】s-t图像中,横坐标为时间,纵坐标为位移,图像的斜率是速度,通过这些性质结合选项分析即可。
15.【答案】 B,C
【解析】【解答】解:汽车匀速运动,牵引力等于阻力,此时P=Fv0=fv0 , 若在t=0时刻将汽车发动机的输出功率调为另一个恒定值,且这个定值比P小,则瞬间牵引力减小,牵引力小于阻力,根据牛顿第二定律可知a= ,则加速度反向减小,故汽车做加速度减小的减速运动,
若在t=0时刻将汽车发动机的输出功率调为另一个恒定值,且这个定值比P大,则根据P=Fv可知瞬间牵引力增大,随着速度增大,牵引力减小,根据牛顿第二定律可知a= ,则加速度减小,故汽车做加速度减小的加速运动,故BC正确,AD错误.
故选:BC.
【分析】本题要分功率变大和变小两种情况,根据P=Fv以及牛顿第二定律分析速度和加速度的变化情况,从而选择图象.
三、填空题
16.【答案】24;﹣2;12
【解析】【解答】解:解:由x=v0t+ at2=24t﹣t2 , 得初速度v0=24m/s,加速度a=﹣2m/s2 .
当物体的速度为0时,由v=v0+at得:
故答案为:24,﹣2,12.
【分析】根据匀变速直线运动的位移时间公式x=v0t+ at2得出质点的初速度和加速度.由速度公式即可求出物体速度为0的时间.
17.【答案】1;﹣2;﹣0.5;24
【解析】【解答】OA段的加速度 ;
BC段的加速度 ;
CD段的加速度 ;
物体在14s内的总位移为图象与时间轴围成的面积,故位移为: ×(4+10)×4- ×4×2=24m;
【分析】v-t图像中,横坐标为时间,纵坐标为速度,图像与时间轴所围成的面积是位移,图像的斜率是加速度,通过这些性质分析即可。
18.【答案】 4;10;4
【解析】【解答】根据匀变速直线运动的公式:
对比:
xA=6+3t +2t2
可得A的加速度为4m/s2
同理对比:xB=10t-t2
可得物体B的初速度为10m/s.当t=2s时,A的位置为xA=20m;B的位置为:xB=16m,所以AB相距为:
【分析】结合题目中给出的物体位移与时间的关系,对比匀变速直线运动公式,求出物体的初速度和加速度,再结合选项分析求解即可。
19.【答案】4;40
【解析】【解答】解:物体自由落体运动,根据位移时间关系公式 有:h= ;
物体自由落体运动,根据速度时间关系公式,着地速度为:v=gt=10×4=40m/s;
故答案为:4,40
【分析】自由落体运动是初速度为零的匀加速直线运动,初速度为零的匀加速直线运动,由h= 即可求出运动的时间,由v=gt即可求出末速度.
20.【答案】2;1;10
【解析】【解答】根据位移公式 ,可得:
第1s内的位移: ①
第2s内的位移: ②
联立两式,可得:v0=1m/s a=2m/s2
第5s内的位移:
故答案为:2,1,10.
【分析】根据位移公式 ,物体第2s内的位移等于前2s内的位移减去第1s内的位移,联立列式可求解
21.【答案】 0.2m/s2
【解析】【解答】遮光板通过第一个光电门的速度 ,遮光板通过第二个光电门的速度 ,则加速度 .
【分析】当运动位移很短时,物体的平均速度等于物体运动的瞬时速度,利用宽度除以挡光的时间即可;结合物体的初末速度,利用加速度定义式求解即可。
四、实验探究题
22.【答案】 (1)交流;0.02
(2)0.36;0.43;0.35
【解析】解:(1)电磁打点计时器的电源应是交流电源,实验室使用我国民用电时,每隔0.02s打一次点,
如果每打5个取一个计数点,即相邻两个计数点间的时间间隔为0.1s.(2)①根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上1点时小车的瞬时速度大小.
v1= m/s=0.36m/s
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上3点时小车的瞬时速度大小.
v3= m/s=0.43m/s②根据加速度定义式得
a= = =0.35m/s2 . 故答案为:(1)交流,0.02;(2)①0.36;0.43;②0.35.
【分析】(1)根据打点计时器的原理结合周期公式,求解。
(2)纸带点分析过程中,中间时刻的瞬时速度等于全程的平均速度,相邻相等时间间隔位移之差恒定。
五、综合题
23.【答案】 (1)解:设木球做自由落体运动的时间为t1 ,
由运动学公式得:h= gt12 ,
解得:t1= = =1s
答:木球做自由落体运动的时间为1s
(2)解:木球入水时的速度:v=gt1=10×1=10m/s
答:木球入水时的速度大小为10m/s
(3)解:木球在水中运动的时间:t2=t﹣t1=1.5﹣1=0.5s,
木球做匀减速运动过程的加速度大小:a= = =20m/s2 ,
游泳池水的深度:h′= t2= ×0.5=2.5m
答:木球在水中运动的加速度的大小为20m/s2 , 游泳池水的深度为2.5m.
【解析】【分析】(1)应用匀变速直线运动的位移公式可以求出自由下落的时间.(2)应用匀变速直线运动的速度公式可以求出木球入水时的速度.(3)应用加速度的定义式可以求出木球在水中的加速度,应用平均速度公式可以求出水的深度.
24.【答案】 (1)解:木箱由静止放到传送带上,开始过程,根据牛顿第二定律得
对木箱:μMg=Ma
a=μg=0.75×10m/s2=7.5m/s2
木箱加速位移: =15m
木箱加速时间: =2s
x1=15m<l=30m 所以还要在传送带上匀速后一段距离
木箱匀速时运动的时间:l﹣x1=vt2
t2= =1s
所以木箱从A运动到传送带另一端B处经历时间t=t1+t2=3s
答:木箱由静止放到传送带上,经过3s时间木箱能够从A运动到传送带的另一端B处
(2)解:设绳P伸直恰好无拉力时木箱的加速度为a0 , 则由牛顿第二定律得
mgtan30°=ma0
代入解得: <7.5m/s2
故小球已经飘起来,绳P的张力大小TP=0
此时有:
代入解得TQ=1.25N
答:木箱放到传送带A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为0和1.25N
【解析】【分析】(1)木箱由静止放到传送带上,水平方向先做受到滑动摩擦力,做匀加速直线运动,由牛顿第二定律求出加速度,由速度公式求出木箱速度与传送带相同时经历的时间和通过的位移,并判断木箱是否有匀速运动过程.如有,求出时间,再求总时间.(2)由牛顿第二定律求出绳P恰好张力时木箱的加速度a0 , 根据a0与木箱加速过程的加速度a的大小比较,判断绳P是否有张力,再由牛顿第二定律求解两绳的张力.
21世纪教育网(www.21cnjy.com)
