冀教版八上数学17.3勾股定理课件(27张ppt)
文档属性
| 名称 | 冀教版八上数学17.3勾股定理课件(27张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 10:29:56 | ||
图片预览






文档简介
(共27张PPT)
直角三角形的性质:
直角三角形的判定:
1:直角三角形两锐角互余;
2:在直角三角形中,斜边上的中线等于 斜边的一半;
3:在直角三角形中,30°角所对的 直角边等于斜边的一半
3:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。(定义)
2:有两个角互余的三角形是直角三角形;
复习回顾
美丽的数学!
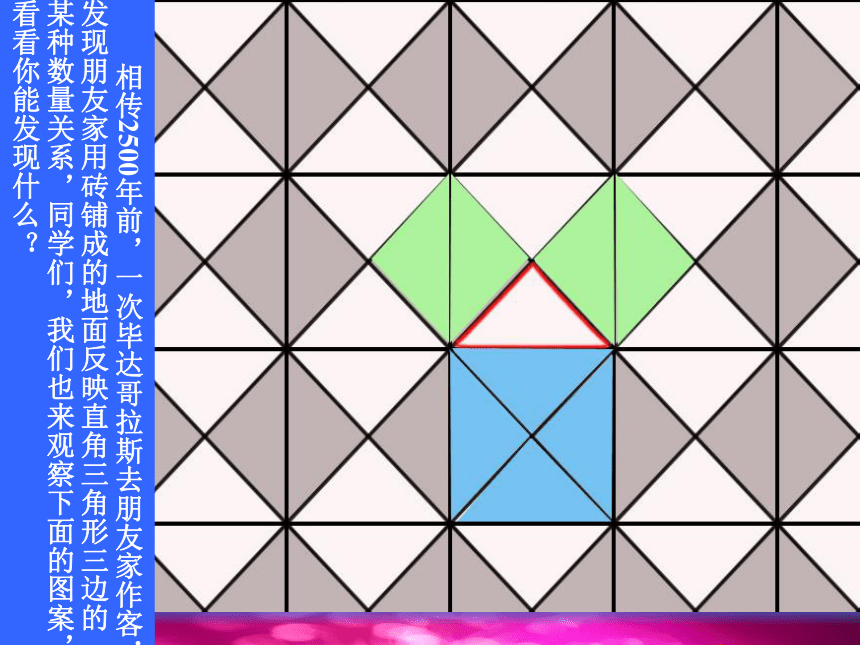
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
A
B
C
C
图乙
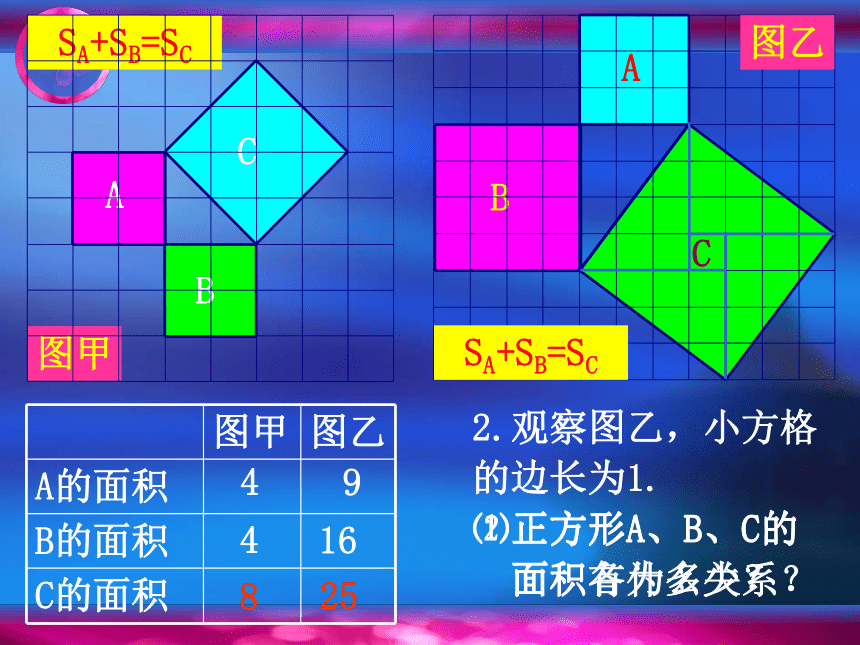
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
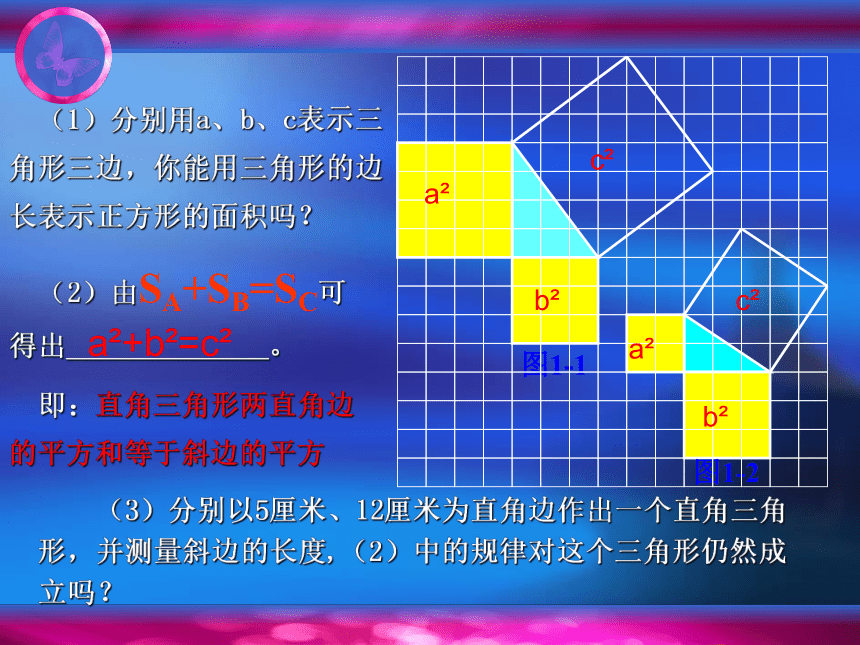
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度,(2)中的规律对这个三角形仍然成立吗?
(1)分别用a、b、c表示三角形三边,你能用三角形的边长表示正方形的面积吗?
(2)由SA+SB=SC可得出 。
即:直角三角形两直角边的平方和等于斜边的平方
图1-1
图1-2
a
a +b =c
b
c
a
b
c
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,所以称作勾股定理.
图2称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 2002年在北京召开的国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图2
图1
17.3 勾股定理(第一课时)
a +b =c
b
a
c
学习目标:
1.掌握勾股定理。
2.了解勾股定理的验证方法,能写出验证过程,体会数形结合思想。
3.运用勾股定理进行解直角三角形。
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a,b,斜边为c,
那么 ;
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
注意:不同三角形中字母可能不同,要看清那条是直角边,那条是斜边
利用拼图来验证勾股定理:
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个以斜边c正方形吗?拼一拼试试看
3.你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4 ab/2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 ab/2-(b- a)2
验证1
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4 ab/2
验证2
对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
验证3
c
a
b
c
a
b
总统证法:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
验证4
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
青朱出入图
朱入
朱出
验证5
东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法
验证6
欧几里得证法
勾
股
定
理
的
证
明
证明方法2:拼三角形
证明方法3:赵爽弦图,
证明方法4:总统加菲尔德法
证明方法1:数方格
证明方法5:刘徽青朱出入图
在直角三角形中,已知两边可以求第三边
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长。
在Rt△ABC中
, 根据勾股定理
解:
B
24
A
C
7
如果将题目变为:
在Rt△ABC中,AB=25, BC=24,求AC的长呢?
25
24
例2 已知等边三角形ABC的边长是6cm, (1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, 根据勾股定理
例3 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
练习
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c= ;
3.如图,在△ABC中,C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?
C
A
B
D
m
n
h
(3)若c=25,b=15,则a= ;
2.等边三角形边长为10,求它的高及面积。
b
a
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
1
1
请欣赏 美丽的勾股树
看一看
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
直角三角形的性质:
直角三角形的判定:
1:直角三角形两锐角互余;
2:在直角三角形中,斜边上的中线等于 斜边的一半;
3:在直角三角形中,30°角所对的 直角边等于斜边的一半
3:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。(定义)
2:有两个角互余的三角形是直角三角形;
复习回顾
美丽的数学!
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
A
B
C
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度,(2)中的规律对这个三角形仍然成立吗?
(1)分别用a、b、c表示三角形三边,你能用三角形的边长表示正方形的面积吗?
(2)由SA+SB=SC可得出 。
即:直角三角形两直角边的平方和等于斜边的平方
图1-1
图1-2
a
a +b =c
b
c
a
b
c
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,所以称作勾股定理.
图2称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 2002年在北京召开的国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图2
图1
17.3 勾股定理(第一课时)
a +b =c
b
a
c
学习目标:
1.掌握勾股定理。
2.了解勾股定理的验证方法,能写出验证过程,体会数形结合思想。
3.运用勾股定理进行解直角三角形。
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a,b,斜边为c,
那么 ;
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
注意:不同三角形中字母可能不同,要看清那条是直角边,那条是斜边
利用拼图来验证勾股定理:
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个以斜边c正方形吗?拼一拼试试看
3.你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4 ab/2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 ab/2-(b- a)2
验证1
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4 ab/2
验证2
对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
验证3
c
a
b
c
a
b
总统证法:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
验证4
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
青朱出入图
朱入
朱出
验证5
东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法
验证6
欧几里得证法
勾
股
定
理
的
证
明
证明方法2:拼三角形
证明方法3:赵爽弦图,
证明方法4:总统加菲尔德法
证明方法1:数方格
证明方法5:刘徽青朱出入图
在直角三角形中,已知两边可以求第三边
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长。
在Rt△ABC中
, 根据勾股定理
解:
B
24
A
C
7
如果将题目变为:
在Rt△ABC中,AB=25, BC=24,求AC的长呢?
25
24
例2 已知等边三角形ABC的边长是6cm, (1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, 根据勾股定理
例3 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
练习
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c= ;
3.如图,在△ABC中,C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?
C
A
B
D
m
n
h
(3)若c=25,b=15,则a= ;
2.等边三角形边长为10,求它的高及面积。
b
a
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
1
1
请欣赏 美丽的勾股树
看一看
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
