2021-2022学年人教版数学八年级上册13.2.2用坐标表示轴对称课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.2.2用坐标表示轴对称课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 649.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
八年级 上册
13.2 画轴对称图形 (第2课时)
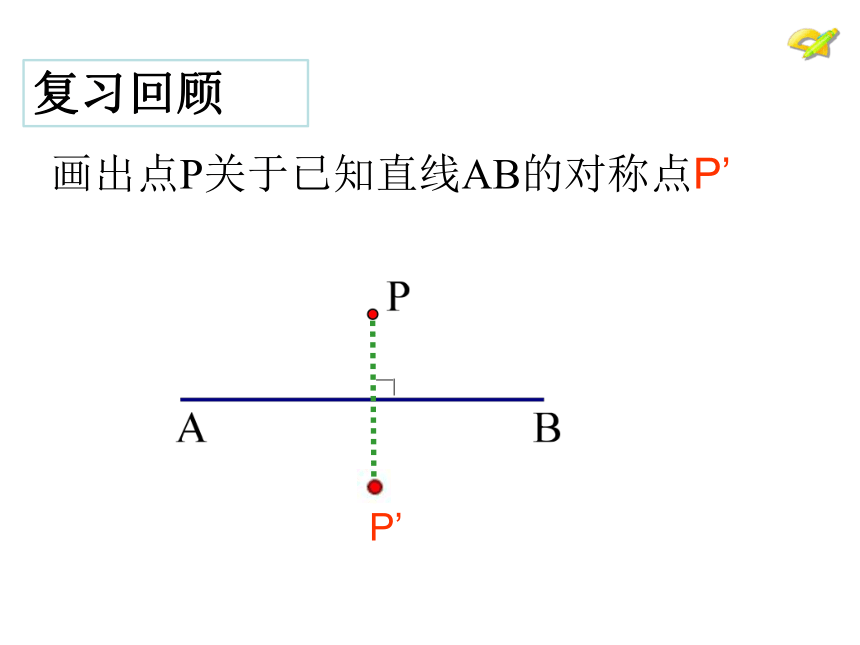
P’
复习回顾
画出点P关于已知直线AB的对称点P’
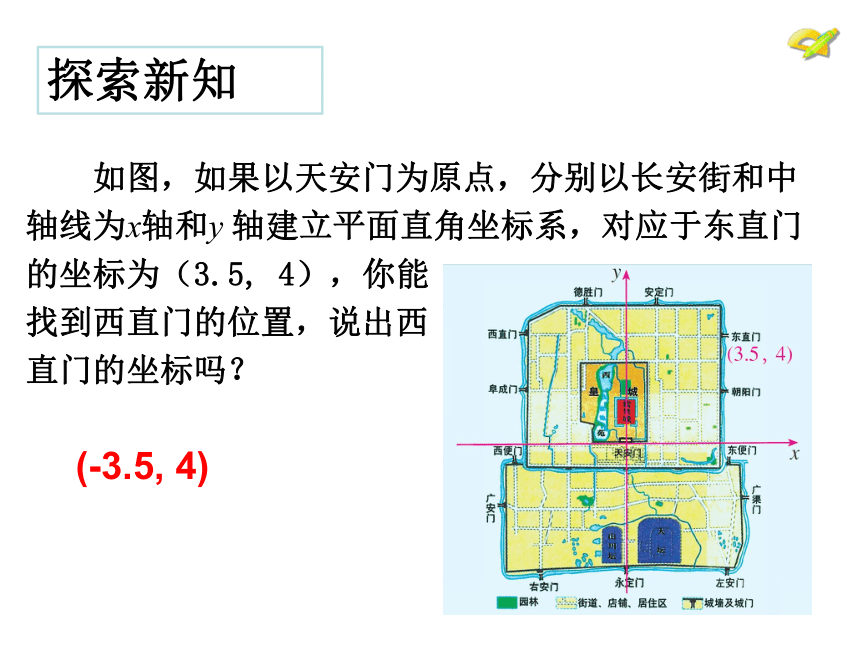
如图,如果以天安门为原点,分别以长安街和中
轴线为x轴和y 轴建立平面直角坐标系,对应于东直门
的坐标为(3.5, 4),你能
找到西直门的位置,说出西
直门的坐标吗?
探索新知
(-3.5, 4)
探索新知
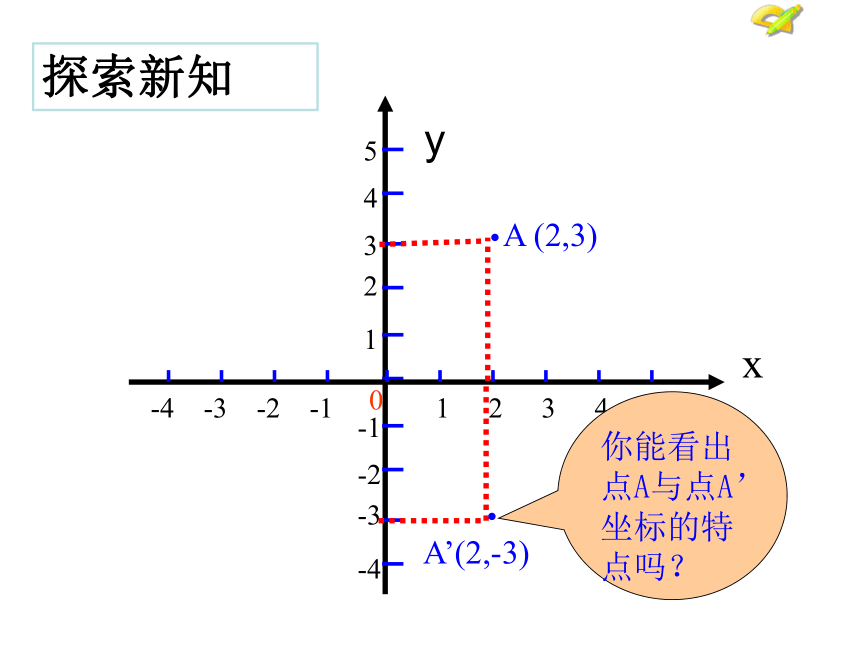
在平面直角坐标系中描出下列各点:
A(2,-3) B(-1,2) C(-6,-5)
D(0.5 ,1) E(4,0) F(0,-3)
在坐标系中画出上面各点关于x轴对称的点
探索新知
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能看出点A与点A’坐标的特点吗?
x
y
探索新知
思考:关于x轴对称的点的坐标具有怎样的关系?
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
探索新知
A(2,-3) B(-1,2) C(-6,-5)
D(0.5 ,1) E(4,0) F(0,-3)
在坐标系中画出上面各点关于y轴对称的点
思考:关于y轴对称的点的坐标具有怎样的关系?
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
归纳总结
★观察发现规律
点(x,y)关于x 轴对称的点的坐标为__________;
点(x,y)关于y轴对称的点的坐标为___________.
(x, - y)
(- x, y)
应用新知
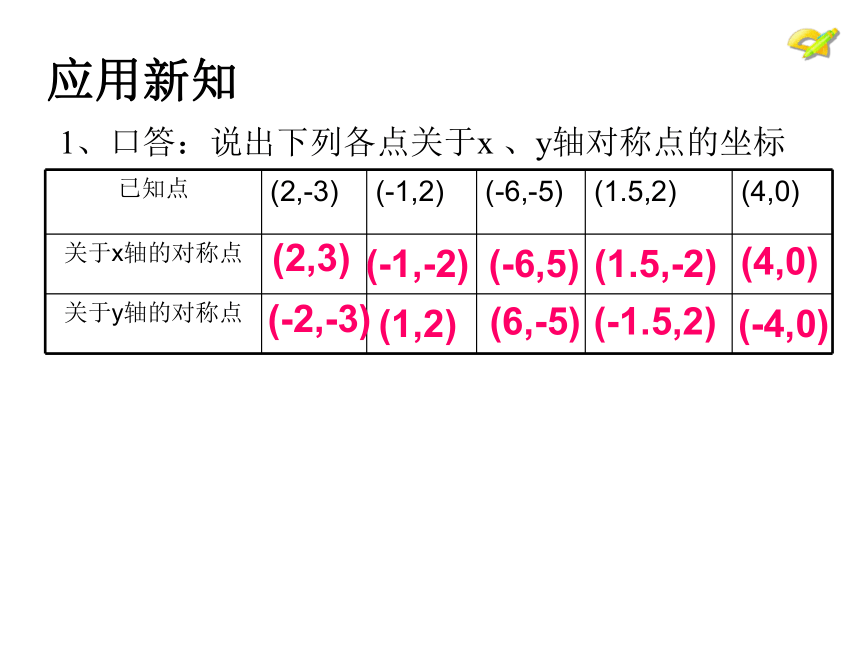
1、口答:说出下列各点关于x 、y轴对称点的坐标
已知点 (2,-3) (-1,2) (-6,-5) (1.5,2) (4,0)
关于x轴的对称点
关于y轴的对称点
(2,3)
(-1,-2)
(-6,5)
(1.5,-2)
(4,0)
(-2,-3)
(1,2)
(6,-5)
(-1.5,2)
(-4,0)
应用新知
2、口答:根据点的坐标特点判断点的位置关系:
P P′
(6,1) 与(-6,1)
(-1,6) 与(-1,-6)
(-6,-5)与(-6,5)
(a,b) 与(-a,b)
(m,-n)与(-m,-n)
(2a,-1) 与(2a,1)
关于y轴对称
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
关于x轴对称
(1)若点P(m,-3)与点P′(8,n)
关于x 轴对称,则m =______,n=_______;
(2)若点P(-x,y)与点P′(1,6)
关于y 轴对称,则x =______,y=______.
应用新知
3、运用规律求未知数的值(口答)
8
3
1
6
(计算过程书写在学案上)
(1)若点P(2a+b,-3a)与点P′(8,b+2)
关于x 轴对称,则a =______,b=_______;
(2)若点P(2a+b,-3a)与点P′(8,b+2)
关于y 轴对称,则a =______,b=______.
应用新知
4、运用变化规律求未知数的值
2
4
6
-20
例 如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.
x
y
1
1
O
A
B
C
D
应用新知
5、运用变化规律作图
x
y
1
1
O
A
B
C
D
解:依次连接 , , , ,
就可得到与四边形ABCD
关于y轴对称的四边形
.
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
应用新知
5、运用变化规律作图
请在图上画出四边形ABCD 关于x 轴对称的图形.
x
y
1
1
O
A
B
C
D
应用新知
5、运用变化规律作图
各顶点关于y轴对称点的坐标:
A′(-5,1),
B′(-2,1),
C′(-2,5),
D′(-5,4).
先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x 轴或y 轴对称的图形的方法
和步骤.
总结归纳,形成能力
6、如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形.
提升能力,展示自我
(1)在平面直角坐标系中,已知点关于x 轴或y 轴的
对称点的坐标有什么变化规律
课堂总结
本节课我们学习了哪些内容?
(2)如何判断两个点是否关于x 轴或y 轴对称?
(3)说一说画一个图形关于x 轴或y 轴对称的图形的方法和步骤.
完成学案巩固练习的1-6题
课堂自我检测
1、课本上习题13.2的第3、4、5题.
2、学案上巩固练习的7-9题
——预计用时15分钟
布置作业
思考题:点A(-4,1),B(-1,3),C(x, y)关于直线x=1和直线y=-1对称的点坐标分别是什么?
八年级 上册
13.2 画轴对称图形 (第2课时)
P’
复习回顾
画出点P关于已知直线AB的对称点P’
如图,如果以天安门为原点,分别以长安街和中
轴线为x轴和y 轴建立平面直角坐标系,对应于东直门
的坐标为(3.5, 4),你能
找到西直门的位置,说出西
直门的坐标吗?
探索新知
(-3.5, 4)
探索新知
在平面直角坐标系中描出下列各点:
A(2,-3) B(-1,2) C(-6,-5)
D(0.5 ,1) E(4,0) F(0,-3)
在坐标系中画出上面各点关于x轴对称的点
探索新知
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能看出点A与点A’坐标的特点吗?
x
y
探索新知
思考:关于x轴对称的点的坐标具有怎样的关系?
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
探索新知
A(2,-3) B(-1,2) C(-6,-5)
D(0.5 ,1) E(4,0) F(0,-3)
在坐标系中画出上面各点关于y轴对称的点
思考:关于y轴对称的点的坐标具有怎样的关系?
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
归纳总结
★观察发现规律
点(x,y)关于x 轴对称的点的坐标为__________;
点(x,y)关于y轴对称的点的坐标为___________.
(x, - y)
(- x, y)
应用新知
1、口答:说出下列各点关于x 、y轴对称点的坐标
已知点 (2,-3) (-1,2) (-6,-5) (1.5,2) (4,0)
关于x轴的对称点
关于y轴的对称点
(2,3)
(-1,-2)
(-6,5)
(1.5,-2)
(4,0)
(-2,-3)
(1,2)
(6,-5)
(-1.5,2)
(-4,0)
应用新知
2、口答:根据点的坐标特点判断点的位置关系:
P P′
(6,1) 与(-6,1)
(-1,6) 与(-1,-6)
(-6,-5)与(-6,5)
(a,b) 与(-a,b)
(m,-n)与(-m,-n)
(2a,-1) 与(2a,1)
关于y轴对称
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
关于x轴对称
(1)若点P(m,-3)与点P′(8,n)
关于x 轴对称,则m =______,n=_______;
(2)若点P(-x,y)与点P′(1,6)
关于y 轴对称,则x =______,y=______.
应用新知
3、运用规律求未知数的值(口答)
8
3
1
6
(计算过程书写在学案上)
(1)若点P(2a+b,-3a)与点P′(8,b+2)
关于x 轴对称,则a =______,b=_______;
(2)若点P(2a+b,-3a)与点P′(8,b+2)
关于y 轴对称,则a =______,b=______.
应用新知
4、运用变化规律求未知数的值
2
4
6
-20
例 如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.
x
y
1
1
O
A
B
C
D
应用新知
5、运用变化规律作图
x
y
1
1
O
A
B
C
D
解:依次连接 , , , ,
就可得到与四边形ABCD
关于y轴对称的四边形
.
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
应用新知
5、运用变化规律作图
请在图上画出四边形ABCD 关于x 轴对称的图形.
x
y
1
1
O
A
B
C
D
应用新知
5、运用变化规律作图
各顶点关于y轴对称点的坐标:
A′(-5,1),
B′(-2,1),
C′(-2,5),
D′(-5,4).
先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x 轴或y 轴对称的图形的方法
和步骤.
总结归纳,形成能力
6、如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形.
提升能力,展示自我
(1)在平面直角坐标系中,已知点关于x 轴或y 轴的
对称点的坐标有什么变化规律
课堂总结
本节课我们学习了哪些内容?
(2)如何判断两个点是否关于x 轴或y 轴对称?
(3)说一说画一个图形关于x 轴或y 轴对称的图形的方法和步骤.
完成学案巩固练习的1-6题
课堂自我检测
1、课本上习题13.2的第3、4、5题.
2、学案上巩固练习的7-9题
——预计用时15分钟
布置作业
思考题:点A(-4,1),B(-1,3),C(x, y)关于直线x=1和直线y=-1对称的点坐标分别是什么?
