2021—2022学年人教版数学九年级上册24.1.4圆周角(2) 课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册24.1.4圆周角(2) 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 351.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 10:32:45 | ||
图片预览



文档简介
(共17张PPT)
24.1.4圆周角(2)
——圆周角定理的推论和圆内接多边形
A
O
B
C
A
O
B
C
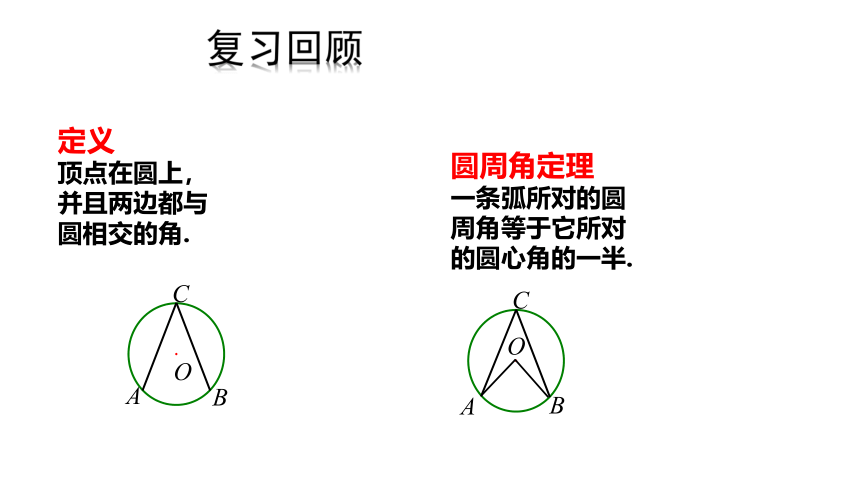
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
定义
顶点在圆上,并且两边都与圆相交的角.
复习回顾
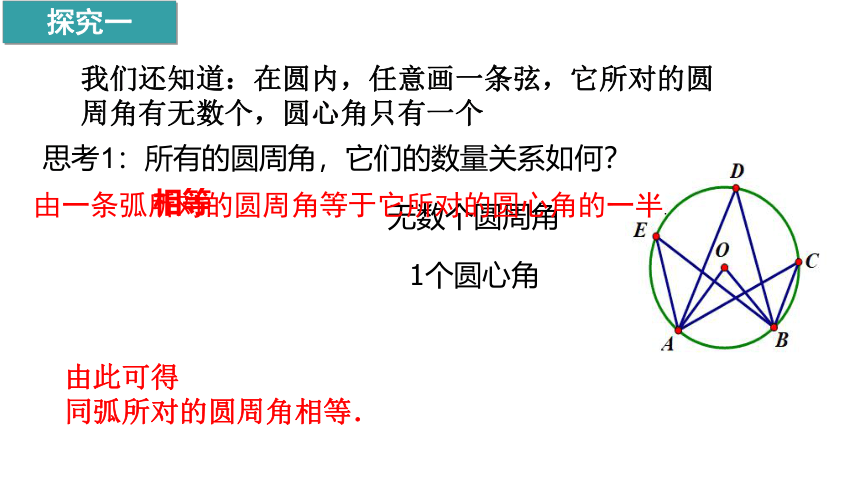
我们还知道:在圆内,任意画一条弦,它所对的圆周角有无数个,圆心角只有一个
无数个圆周角
1个圆心角
思考1:所有的圆周角,它们的数量关系如何?
探究一
相等
由一条弧所对的圆周角等于它所对的圆心角的一半.
由此可得
同弧所对的圆周角相等.
思考2:等弧所对的圆周角相等吗
●
O
F
D
E
B
A
C
如图在 O中,如果 AB=DE,那么它们所对的圆周角 ∠ACB与∠DFE相等吗?
相等
圆周角定理推论1:
同弧或等弧所对的圆周角相等.
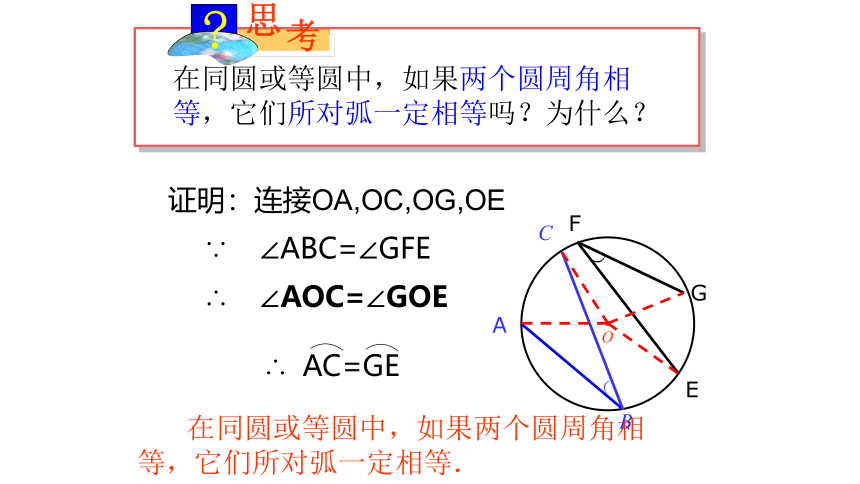
在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等吗?为什么?
思
考
在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.
·
C
B
O
A
F
G
E
(
(
证明:连接OA,OC,OG,OE
∵ ∠ABC=∠GFE
∴ ∠AOC=∠GOE
∴ AC=GE
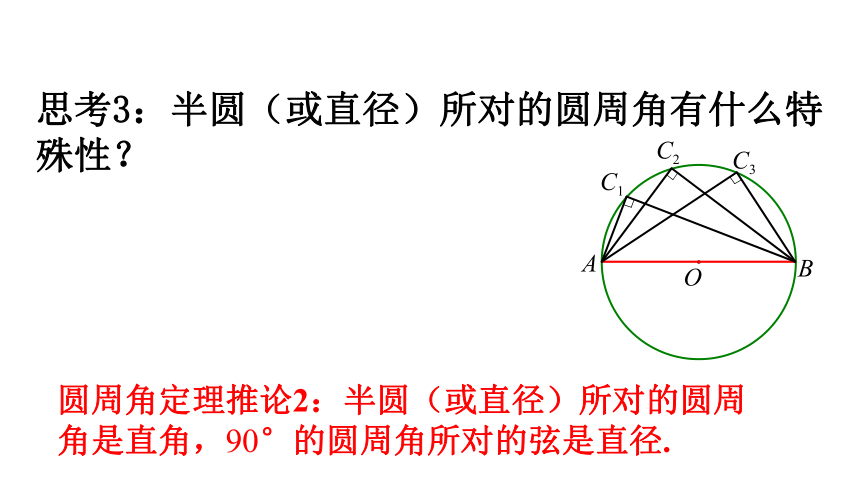
思考3:半圆(或直径)所对的圆周角有什么特殊性?
圆周角定理推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
C1
A
O
B
C2
C3
例: 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,
ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
A
C
B
D
O
典例讲解
解:如图, 连接OD
∵ AB 是⊙O 的直径
∴ ∠ACB=∠ADB=90°
在Rt△ABC中,
∵ CD 平分 ACB,
∴ ACD= BCD,
∴ AOD= BOD .
∴ AD=BD.
在 Rt△ABD 中,
AD2+BD2=AB2 ,
∴ AD=BD=
= (cm).
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形
探究二
以下是圆内接多边形是哪个?并说出理由
练一练
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180
想一想:
如何证明你的猜想呢?
C
A
O
D
B
证明:连接OA,OC.
同理
又
1
2
C
A
D
B
O
则
C
B
A
D
性质:
圆内接四边形的对角互补.
C
B
A
D
E
延伸:
圆内接四边形的任意一个外角等于它的内对角.
O
如图, 在⊙O中,B是AC上的一点,∠AOC=n°, ∠ABC=m°,那么m,n有什么关系?
⌒
D
1、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拔:由同弧来找相等的圆周角
自我检测
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
A
O
B
C
D
·
E
A
3、若ABCD为圆内接四边形,下列可能成立的是( )
A. ∠A∶∠B∶∠C∶∠D 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D 4∶3∶2∶1
A
O
B
C
D
·
比较∠A ∠C 和 比较∠A ∠C 和∠B ∠D所占的份数是否相等即可.
∠B ∠D所占的份数是否相等即可.
B
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
圆周角与直
线的关系
课堂小结
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
半圆或直径所对的圆周角都相等,都等于90°(直角).
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1、同弧或等弧所对的圆周角相等
2、90°的圆周角所对的弦是直径;
3、圆内接四边形的对角互补.
24.1.4圆周角(2)
——圆周角定理的推论和圆内接多边形
A
O
B
C
A
O
B
C
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
定义
顶点在圆上,并且两边都与圆相交的角.
复习回顾
我们还知道:在圆内,任意画一条弦,它所对的圆周角有无数个,圆心角只有一个
无数个圆周角
1个圆心角
思考1:所有的圆周角,它们的数量关系如何?
探究一
相等
由一条弧所对的圆周角等于它所对的圆心角的一半.
由此可得
同弧所对的圆周角相等.
思考2:等弧所对的圆周角相等吗
●
O
F
D
E
B
A
C
如图在 O中,如果 AB=DE,那么它们所对的圆周角 ∠ACB与∠DFE相等吗?
相等
圆周角定理推论1:
同弧或等弧所对的圆周角相等.
在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等吗?为什么?
思
考
在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.
·
C
B
O
A
F
G
E
(
(
证明:连接OA,OC,OG,OE
∵ ∠ABC=∠GFE
∴ ∠AOC=∠GOE
∴ AC=GE
思考3:半圆(或直径)所对的圆周角有什么特殊性?
圆周角定理推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
C1
A
O
B
C2
C3
例: 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,
ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
A
C
B
D
O
典例讲解
解:如图, 连接OD
∵ AB 是⊙O 的直径
∴ ∠ACB=∠ADB=90°
在Rt△ABC中,
∵ CD 平分 ACB,
∴ ACD= BCD,
∴ AOD= BOD .
∴ AD=BD.
在 Rt△ABD 中,
AD2+BD2=AB2 ,
∴ AD=BD=
= (cm).
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形
探究二
以下是圆内接多边形是哪个?并说出理由
练一练
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180
想一想:
如何证明你的猜想呢?
C
A
O
D
B
证明:连接OA,OC.
同理
又
1
2
C
A
D
B
O
则
C
B
A
D
性质:
圆内接四边形的对角互补.
C
B
A
D
E
延伸:
圆内接四边形的任意一个外角等于它的内对角.
O
如图, 在⊙O中,B是AC上的一点,∠AOC=n°, ∠ABC=m°,那么m,n有什么关系?
⌒
D
1、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拔:由同弧来找相等的圆周角
自我检测
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
A
O
B
C
D
·
E
A
3、若ABCD为圆内接四边形,下列可能成立的是( )
A. ∠A∶∠B∶∠C∶∠D 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D 4∶3∶2∶1
A
O
B
C
D
·
比较∠A ∠C 和 比较∠A ∠C 和∠B ∠D所占的份数是否相等即可.
∠B ∠D所占的份数是否相等即可.
B
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
圆周角与直
线的关系
课堂小结
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
半圆或直径所对的圆周角都相等,都等于90°(直角).
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1、同弧或等弧所对的圆周角相等
2、90°的圆周角所对的弦是直径;
3、圆内接四边形的对角互补.
同课章节目录
