2021-2022学年度北师大版九年级数学下册1.2 30°,45°,60°角的三角函数值课件((共17张PPT))
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册1.2 30°,45°,60°角的三角函数值课件((共17张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 956.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 16:18:13 | ||
图片预览





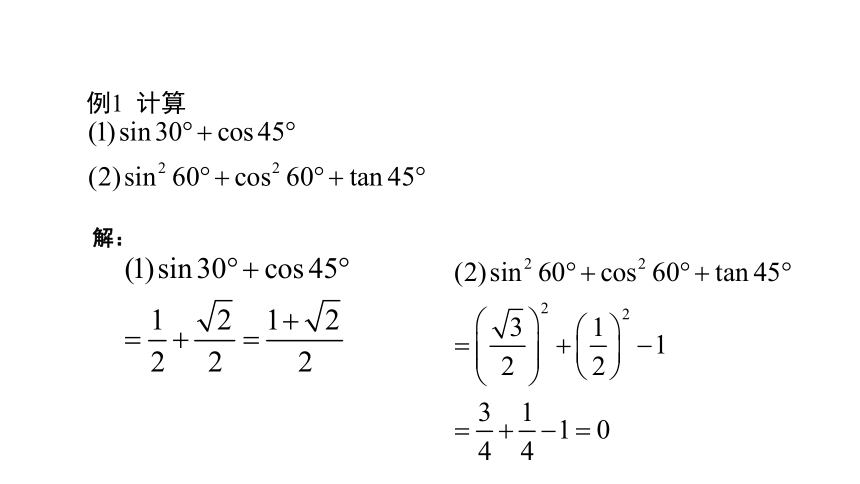
文档简介
(共17张PPT)
第一单元·第2课
30°,45°,60°角的三角函数值
在 Rt△ABC中,∠C=90°。
(1)三条边之间的关系是 ∠A+∠B= 。
(2)sin A= ,cos A= , tan A= 。
sin B= ,cos B= , tan B= 。
(3)若其中一个角为30°,则= 。
复习巩固
为了测量一棵大树的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺.
请你设计一个测量方案,能测出一棵大树的高度.
新知探究
让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°的邻边和水平方向平行,用卷尺测出AB的长度和BE的长度,因为DE=AB,所以只需在Rt△CDA中求出CD的长度即可.
tan30°=
则CD=a·tan30°
新知探究
探索30°角的三角函数值
①观察一副三角尺,其中有几个锐角 它们分别等于多少度
┌
┌
② sin30°等于多少呢 你是怎样得到的 与同伴交流.
③cos30°等于多少 tan30°呢
我们求出了30°角的三个三角函数值,还有两个特殊角——45°、60°,它们的三角函数值分别是多少 你是如何得到的
45°
60°
新知探究
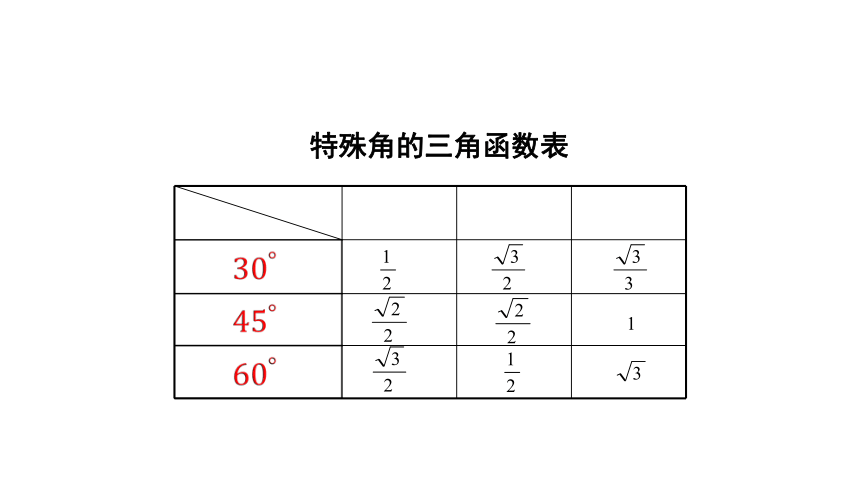
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
特殊角的三角函数表
新知探究
例1 计算
解:
新知探究
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
新知探究
如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
D
A
C
O
B
┌
2.5
新知探究
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD = 2.5m ,
解:如图,根据题意可知,
新知探究
计算:
知识运用
3.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高 精确到0.1 m,其中
知识运用
1.已知α为锐角,且 ,则 α=_____度.
50
分析:根据特殊角的三角函数值即可求得α角的度数。
课堂练习
2.如图,公园里有一块如四边形 的草地,测得 BC=CD=10m,∠B=∠C=120° ,∠A=45° ,则这块草地的面积为__________ .
分析:连接BD,找到特殊角的三角形,再
利用三角形面积公式即可求解。
课堂练习
3.如图,已知 ∠AOB=60°,点 P在边OA上,OP=12 ,
点 M、N 在边 OB上,PM=PN ,MN=2 ,求 OM.
分析:过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD-MD即可求出OM的长.
课堂练习
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°= = ,OP=12则OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
课堂练习
再见
第一单元·第2课
30°,45°,60°角的三角函数值
在 Rt△ABC中,∠C=90°。
(1)三条边之间的关系是 ∠A+∠B= 。
(2)sin A= ,cos A= , tan A= 。
sin B= ,cos B= , tan B= 。
(3)若其中一个角为30°,则= 。
复习巩固
为了测量一棵大树的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺.
请你设计一个测量方案,能测出一棵大树的高度.
新知探究
让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°的邻边和水平方向平行,用卷尺测出AB的长度和BE的长度,因为DE=AB,所以只需在Rt△CDA中求出CD的长度即可.
tan30°=
则CD=a·tan30°
新知探究
探索30°角的三角函数值
①观察一副三角尺,其中有几个锐角 它们分别等于多少度
┌
┌
② sin30°等于多少呢 你是怎样得到的 与同伴交流.
③cos30°等于多少 tan30°呢
我们求出了30°角的三个三角函数值,还有两个特殊角——45°、60°,它们的三角函数值分别是多少 你是如何得到的
45°
60°
新知探究
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
特殊角的三角函数表
新知探究
例1 计算
解:
新知探究
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
新知探究
如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
D
A
C
O
B
┌
2.5
新知探究
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD = 2.5m ,
解:如图,根据题意可知,
新知探究
计算:
知识运用
3.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高 精确到0.1 m,其中
知识运用
1.已知α为锐角,且 ,则 α=_____度.
50
分析:根据特殊角的三角函数值即可求得α角的度数。
课堂练习
2.如图,公园里有一块如四边形 的草地,测得 BC=CD=10m,∠B=∠C=120° ,∠A=45° ,则这块草地的面积为__________ .
分析:连接BD,找到特殊角的三角形,再
利用三角形面积公式即可求解。
课堂练习
3.如图,已知 ∠AOB=60°,点 P在边OA上,OP=12 ,
点 M、N 在边 OB上,PM=PN ,MN=2 ,求 OM.
分析:过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD-MD即可求出OM的长.
课堂练习
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°= = ,OP=12则OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
课堂练习
再见
