2021-2022学年度北师大版九年级数学下册课件1.3 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册课件1.3 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 15:12:02 | ||
图片预览






文档简介
(共17张PPT)
第一单元·第3课
三角函数的计算
1、解直角三角形的基本理论依据:
在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c。
(1)边的关系:
a2+b2=c2(勾股定理);
(2)角的关系:
∠A+∠B=90°;
(3)边角关系:
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= 。
复习旧知
1、已知在Rt△ABC中,∠C=90, a=6,解直角三角形。
2、一梯子斜靠在一面墙上。已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
∴∠α≈51°19′4″。
所以梯子与地面所成的锐角约51°19′4″。
= 0.625,
复习旧知
复习巩固
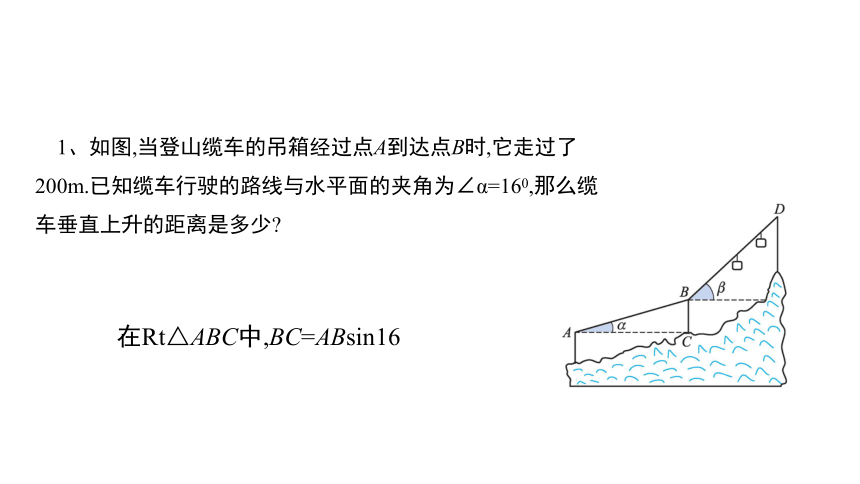
1、如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=160,那么缆车垂直上升的距离是多少
在Rt△ABC中,BC=ABsin16°
新知探究
当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么
新知探究
1.一辆汽车沿着一山坡行驶了150米,其铅直高度上升了25米,求山坡与水平面所成锐角的大小.
复习巩固
解:如图,在Rt△ABC中,AC=6.3 cm,BC=9.8 cm
∴tan B= ≈0.642 9
∴∠B≈
因此,射线与皮肤的夹角约为 。
2、如图,一名患者体内某重要器官后面有一肿瘤。在接受放射性治疗时,为了最大限度的保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤。已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线与皮肤的夹角。
复习巩固
解:∵tan ∠ACD = ≈0.520 8
∴∠ACD≈27.5°
∴∠ACB=∠ACD≈2×27.5°=55°
3、如图,工件上有一V形槽,测得它的上口宽20mm,深19.2mm,求V形角( ∠ACB)的大小。(结果精确到1°)
复习巩固
4 、 一个人由山底爬到山顶,需先爬400的山坡300m,再爬30° 的山坡100m,求山高(结果精确到0.01m).
解:如图,根据题意,可知BC=300 m,BA=100 m,∠C=40°,∠ABF=30°.
在Rt△CBD中,BD=BCsin40°≈300×0.6428
=192.8(m)
所以山高AE=AF+BD=192.8+50=242.8(m).
在Rt△ABF中,AF=ABsin30°=100×0.5
=50(m)
复习巩固
3.求图中避雷针的长度(结果精确到0.01m).
解:如图,根据题意,可知
AB=20m,∠CAB=50°,∠DAB=56°
在Rt△DBA中,DB=ABtan56°
≈20×1.4826
=29.652(m);
在Rt△CBA中,CB=ABtan50°
≈ 20×1.10918
=23.836(m)
所以避雷针的长度DC=DB-CB=29.652-23.836≈5.82(m).
新知探究
通过这节课的学习,你有哪些收获?
感悟反思
如图,某地夏日一天中午,太阳光线与地面成80°角,房屋朝南的窗户高AB=1.8 m,要在窗户外面上方安装一个水平挡板AC,使光线恰好不能直射室内,求挡板AC的宽度.(结果精确到0.01 m)
解:因为tan80°=
所以AC= ≈
=0.317≈0.32(m).
所以水平挡板AC的宽度应为0.32米.
课堂练习
1.用计算器计算cos 44°的结果(精确到0.01)是( )
A 0.90 B 0.72 C 0.69 D 0.66
解析:用计算器解cos44°=0.72.故选B.
课堂练习
2. 计算sin20°-cos20°的值是(保留四位有效数字)( )
A -0.5976 B 0.5976 C -0.5977 D 0.5977
解析:解答: 按MODE,出现:DEG,按sin20-cos20,=后,显示:-0.597 7.故本题选C.
课堂练习
3. 已知∠A为锐角,求满足下列条件的∠A度数.
(1)sin A=0.9816;
(2)tan A=0.1890
解答:(1)∵sin A=0.9816,∴∠A≈79°
(2)∵tan A=0.1890,∴∠A≈11°
课堂练习
再见
第一单元·第3课
三角函数的计算
1、解直角三角形的基本理论依据:
在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c。
(1)边的关系:
a2+b2=c2(勾股定理);
(2)角的关系:
∠A+∠B=90°;
(3)边角关系:
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= 。
复习旧知
1、已知在Rt△ABC中,∠C=90, a=6,解直角三角形。
2、一梯子斜靠在一面墙上。已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
∴∠α≈51°19′4″。
所以梯子与地面所成的锐角约51°19′4″。
= 0.625,
复习旧知
复习巩固
1、如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=160,那么缆车垂直上升的距离是多少
在Rt△ABC中,BC=ABsin16°
新知探究
当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么
新知探究
1.一辆汽车沿着一山坡行驶了150米,其铅直高度上升了25米,求山坡与水平面所成锐角的大小.
复习巩固
解:如图,在Rt△ABC中,AC=6.3 cm,BC=9.8 cm
∴tan B= ≈0.642 9
∴∠B≈
因此,射线与皮肤的夹角约为 。
2、如图,一名患者体内某重要器官后面有一肿瘤。在接受放射性治疗时,为了最大限度的保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤。已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线与皮肤的夹角。
复习巩固
解:∵tan ∠ACD = ≈0.520 8
∴∠ACD≈27.5°
∴∠ACB=∠ACD≈2×27.5°=55°
3、如图,工件上有一V形槽,测得它的上口宽20mm,深19.2mm,求V形角( ∠ACB)的大小。(结果精确到1°)
复习巩固
4 、 一个人由山底爬到山顶,需先爬400的山坡300m,再爬30° 的山坡100m,求山高(结果精确到0.01m).
解:如图,根据题意,可知BC=300 m,BA=100 m,∠C=40°,∠ABF=30°.
在Rt△CBD中,BD=BCsin40°≈300×0.6428
=192.8(m)
所以山高AE=AF+BD=192.8+50=242.8(m).
在Rt△ABF中,AF=ABsin30°=100×0.5
=50(m)
复习巩固
3.求图中避雷针的长度(结果精确到0.01m).
解:如图,根据题意,可知
AB=20m,∠CAB=50°,∠DAB=56°
在Rt△DBA中,DB=ABtan56°
≈20×1.4826
=29.652(m);
在Rt△CBA中,CB=ABtan50°
≈ 20×1.10918
=23.836(m)
所以避雷针的长度DC=DB-CB=29.652-23.836≈5.82(m).
新知探究
通过这节课的学习,你有哪些收获?
感悟反思
如图,某地夏日一天中午,太阳光线与地面成80°角,房屋朝南的窗户高AB=1.8 m,要在窗户外面上方安装一个水平挡板AC,使光线恰好不能直射室内,求挡板AC的宽度.(结果精确到0.01 m)
解:因为tan80°=
所以AC= ≈
=0.317≈0.32(m).
所以水平挡板AC的宽度应为0.32米.
课堂练习
1.用计算器计算cos 44°的结果(精确到0.01)是( )
A 0.90 B 0.72 C 0.69 D 0.66
解析:用计算器解cos44°=0.72.故选B.
课堂练习
2. 计算sin20°-cos20°的值是(保留四位有效数字)( )
A -0.5976 B 0.5976 C -0.5977 D 0.5977
解析:解答: 按MODE,出现:DEG,按sin20-cos20,=后,显示:-0.597 7.故本题选C.
课堂练习
3. 已知∠A为锐角,求满足下列条件的∠A度数.
(1)sin A=0.9816;
(2)tan A=0.1890
解答:(1)∵sin A=0.9816,∴∠A≈79°
(2)∵tan A=0.1890,∴∠A≈11°
课堂练习
再见
