西藏自治区日喀则市南木林高级中学2022届高三上学期第三次月考数学(文)试卷(Word版含答案)
文档属性
| 名称 | 西藏自治区日喀则市南木林高级中学2022届高三上学期第三次月考数学(文)试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 20:05:38 | ||
图片预览




文档简介
日喀则市南木林高级中学2022届高三年级第三次月考试卷
考试方式:闭卷 年级: 高三 学科: 文数
注意事项:
1、本试题全部为笔答题,共 4 页,满分 150 分,考试时间 120 分钟。
2、答卷前将密封线内的项目填写清楚,密封线内禁止答题。
3、用钢笔或签字笔直接答在试卷(或答题纸上)。
4、本试题为闭卷考试,请考生勿将课本进入考场。
一、单选题
1.设集合,,则( )
A. B. C. D.
2.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.空气质量AQI指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图所示的是某市4月1日~20日空气质量AQI指数变化的折线图,则下列说法中错误的是( )
A.这20天中空气质量最好的是4月17日
B.这20天空气质量AQI指数的极差是240
C.总体来说,该市4月份上旬的空气质量比中旬的空气质量好
D.这20天的空气质量AQI指数数据中随机抽出一天的数据,空气质量为“优良”的概率是0.5
4.已知角的终边过点,则的值为( )
A. B. C. D.
5.将容量为n的样本中的数据分成6组,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n的值为( )
A.50 B.60 C.70 D.80
6.已知x,y满足约束条件,则的最大值为( )
A.-21 B.3 C.6 D.9
7.同时抛三枚普通的硬币,出现“两个正面一个反面”的概率是( )
A. B. C. D.
8.等差数列的前项和为,若,,则( )
A. B. C. D.
9.某大型建筑工地因施工噪音过大,被周围居民投诉.现环保局要求其整改,降低声强.已知声强(单位:))表示声音在传播途径中每平方米面积上的声能流密度,声强级(单位:)与声强的函数关系式为,其中为正实数.已知时,.若整改后的施工噪音的声强为原声强的,则整改后的施工噪音的声强级降低了( ) A. B. C. D.
10.已知,,,则,,的大小关系为( )
A. B. C. D.
11.已知双曲线的虚轴长是实轴长的倍,则其顶点到渐近线的距离为( )
A. B. C. D.
12.已知函数,且此函数的图像如图所示,则此函数的解析式可以是( )
A. B.
C. D.
2、填空题
13.若,均为单位向量,且,则____________.
14.以双曲线的右焦点为焦点的抛物线的标准方程是____.
15.设是数列的前n项和,满足,且,则______.
16.长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为__________.
3、解答题
17.在中,角A、B、C的对边分别为a、b、c,且.
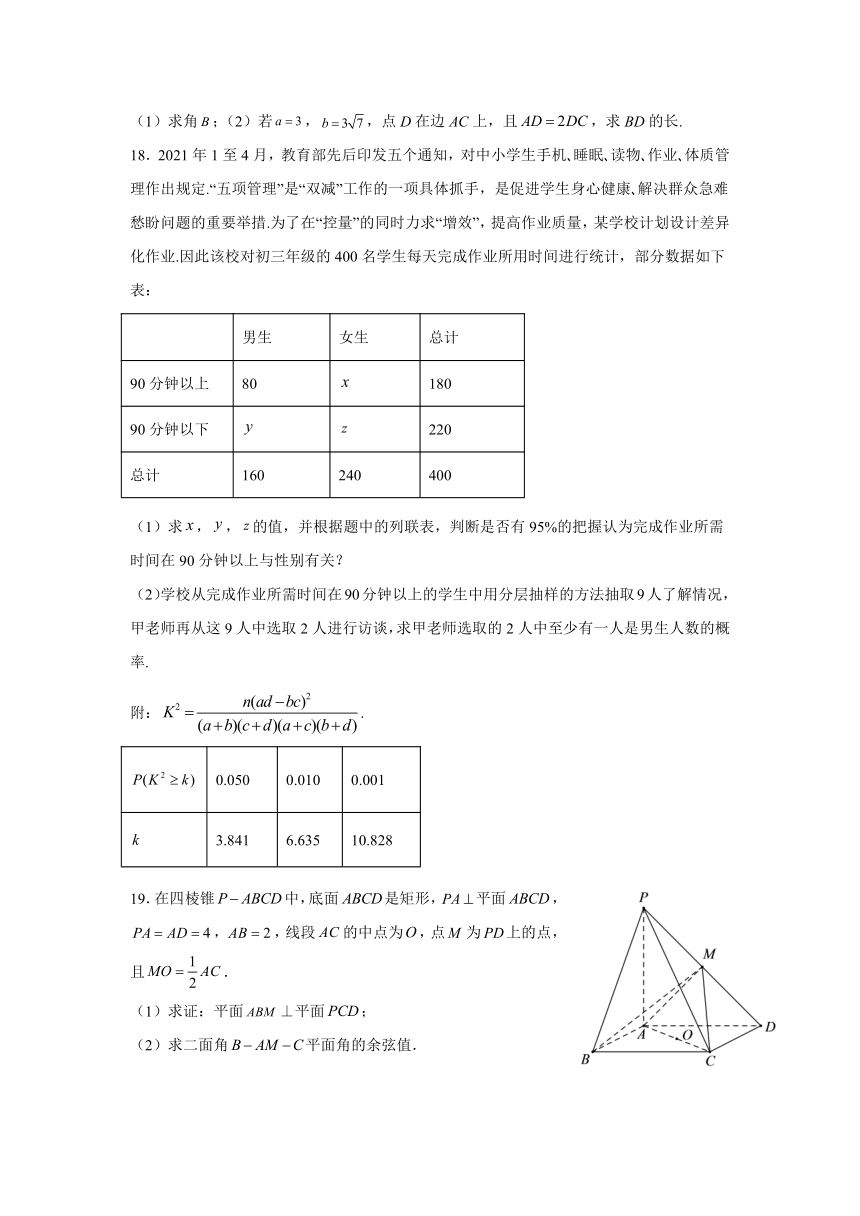
(1)求角;(2)若,,点D在边AC上,且,求BD的长.
18.2021年1至4月,教育部先后印发五个通知,对中小学生手机 睡眠 读物 作业 体质管理作出规定.“五项管理”是“双减”工作的一项具体抓手,是促进学生身心健康 解决群众急难愁盼问题的重要举措.为了在“控量”的同时力求“增效”,提高作业质量,某学校计划设计差异化作业.因此该校对初三年级的400名学生每天完成作业所用时间进行统计,部分数据如下表:
男生 女生 总计
90分钟以上 80 180
90分钟以下 220
总计 160 240 400
(1)求,,的值,并根据题中的列联表,判断是否有95%的把握认为完成作业所需时间在90分钟以上与性别有关?
(2)学校从完成作业所需时间在90分钟以上的学生中用分层抽样的方法抽取9人了解情况,甲老师再从这9人中选取2人进行访谈,求甲老师选取的2人中至少有一人是男生人数的概率.
附:.
0.050 0.010 0.001
3.841 6.635 10.828
19.在四棱锥中,底面是矩形,平面,,,线段的中点为,点为上的点,且.
(1)求证:平面⊥平面;
(2)求二面角平面角的余弦值.
20.已知函数,.
(1)当时,求函数在处的切线方程;(2)讨论函数的单调性;
(3)当函数有两个极值点,,且.证明: .
21.已知为坐标原点,椭圆,其右焦点为,为椭圆(一象限部分)上一点,为中点,,面积为.
(1)求椭圆的方程;
(2)过做圆两条切线,切点分别为,求的值.
22.在直角坐标系中,已知曲线C:(为参数),以坐标原点为极点,以轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线C的普通方程和直线的直角坐标方程;
(2)求曲线C与直线交点的极坐标().
23.已知函数.
(1)当时,解不等式;
(2)若在,使得不等式成立,求实数a的取值范围.
2022届高三年级第三次月考 文数 答案
填空题
13. 14. 15. 16.
解答题
17.
(1)
∵,∴,∵,∴.
(2)设,,则
在中,.
在中:①
在中:②
①+②×2:,综上.
18.
(1)由可得;
由可得;由可得;
所以 列联表如下:
男生 女生 合计
90分钟以上 80 100 180
90分钟以下 80 140 220
合计 160 240 400
,
所以没有95%的把握认为完成作业所需时间在90分钟以上与性别有关.
(2)抽取的9人中,男生:人,女生:人,
至少有一人为男生人数的情况分为:
①男生1人,女生1人;②2人都是男生
所以9人中选择2人共结果有36种.其9人中4个男生记为a.b.c.d.而5个女生记为1.2.3.4.5其中任选2人的结果为
(a,b)(a,c)(a,d)(a,1)(a,2)(a,3)(a,4)(a,5)...8个
(b,c)(b,d)(b,1)(b,2)(b,3)(b,4)(b,5)...7个
... ...
...1个
共8+7+...+1=36
其中1男1女的有5+5+5+5=20个,而2人都是男的有3+2+1=6
所以概率
19.
(1)由,则,
由平面,面,则,
又,,
∴平面,面,
∴,,面,
∴平面 ,面,
∴平面⊥平面.
(2)以为原点,为轴,为轴,为轴建立空间直角坐标系,
∴,,,,
由(1)知:平面,且为的中点,故,又,,
∴平面,则为平面的法向量,即为平面的法向量且,
设平面的法向量为,由,又,
∴,令,则,
设平面与平面所成二面角的大小为,则
20.
解:(Ⅰ)当时,.
∴.
,.
.
∴在处的切线方程.
(Ⅱ)的定义域.
;
①当时,即,
,此时在单调递减;
②当时,即或,
(i)当时,
∴在,单调递减,
在单调递增.
(ii)当时,
∴在单调递减;
综上所述,当时,在单调递减;
当时,在,单调递减,
在单调递增.
(Ⅲ)由(Ⅱ)知,当时,有两个极值点,,且满足:,
由题意知,.
∴
令.
则.
在单调递增,在单调递减.
∴.
即.
21.
(1)设椭圆左焦点为,则,
又,则,
又,
则,
则,
故,
则椭圆方程为.
(2),则,
代入椭圆得,故,,
又过做圆两条切线,切点分别为,
则,
设,,
22.
(1)曲线的参数方程消去参数可得:
故曲线化为普通方程为:,
由,得,
结合
所以直线的直角坐标方程为.
(2)的普通方程可化为,联立,
解得或,
化为极坐标可得,.
23.
(1)当时,.
当时,,解得,结合得;
当时,,解得,结合得;
当时,,解得,结合得.
∴原不等式的解集为.
(2)当时,可化为,
∴或,
即存在,使得,或.
,因为,所以∴,
,因为,所以,所以,
∴实数a的取值范围为.
考试方式:闭卷 年级: 高三 学科: 文数
注意事项:
1、本试题全部为笔答题,共 4 页,满分 150 分,考试时间 120 分钟。
2、答卷前将密封线内的项目填写清楚,密封线内禁止答题。
3、用钢笔或签字笔直接答在试卷(或答题纸上)。
4、本试题为闭卷考试,请考生勿将课本进入考场。
一、单选题
1.设集合,,则( )
A. B. C. D.
2.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.空气质量AQI指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图所示的是某市4月1日~20日空气质量AQI指数变化的折线图,则下列说法中错误的是( )
A.这20天中空气质量最好的是4月17日
B.这20天空气质量AQI指数的极差是240
C.总体来说,该市4月份上旬的空气质量比中旬的空气质量好
D.这20天的空气质量AQI指数数据中随机抽出一天的数据,空气质量为“优良”的概率是0.5
4.已知角的终边过点,则的值为( )
A. B. C. D.
5.将容量为n的样本中的数据分成6组,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n的值为( )
A.50 B.60 C.70 D.80
6.已知x,y满足约束条件,则的最大值为( )
A.-21 B.3 C.6 D.9
7.同时抛三枚普通的硬币,出现“两个正面一个反面”的概率是( )
A. B. C. D.
8.等差数列的前项和为,若,,则( )
A. B. C. D.
9.某大型建筑工地因施工噪音过大,被周围居民投诉.现环保局要求其整改,降低声强.已知声强(单位:))表示声音在传播途径中每平方米面积上的声能流密度,声强级(单位:)与声强的函数关系式为,其中为正实数.已知时,.若整改后的施工噪音的声强为原声强的,则整改后的施工噪音的声强级降低了( ) A. B. C. D.
10.已知,,,则,,的大小关系为( )
A. B. C. D.
11.已知双曲线的虚轴长是实轴长的倍,则其顶点到渐近线的距离为( )
A. B. C. D.
12.已知函数,且此函数的图像如图所示,则此函数的解析式可以是( )
A. B.
C. D.
2、填空题
13.若,均为单位向量,且,则____________.
14.以双曲线的右焦点为焦点的抛物线的标准方程是____.
15.设是数列的前n项和,满足,且,则______.
16.长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为__________.
3、解答题
17.在中,角A、B、C的对边分别为a、b、c,且.
(1)求角;(2)若,,点D在边AC上,且,求BD的长.
18.2021年1至4月,教育部先后印发五个通知,对中小学生手机 睡眠 读物 作业 体质管理作出规定.“五项管理”是“双减”工作的一项具体抓手,是促进学生身心健康 解决群众急难愁盼问题的重要举措.为了在“控量”的同时力求“增效”,提高作业质量,某学校计划设计差异化作业.因此该校对初三年级的400名学生每天完成作业所用时间进行统计,部分数据如下表:
男生 女生 总计
90分钟以上 80 180
90分钟以下 220
总计 160 240 400
(1)求,,的值,并根据题中的列联表,判断是否有95%的把握认为完成作业所需时间在90分钟以上与性别有关?
(2)学校从完成作业所需时间在90分钟以上的学生中用分层抽样的方法抽取9人了解情况,甲老师再从这9人中选取2人进行访谈,求甲老师选取的2人中至少有一人是男生人数的概率.
附:.
0.050 0.010 0.001
3.841 6.635 10.828
19.在四棱锥中,底面是矩形,平面,,,线段的中点为,点为上的点,且.
(1)求证:平面⊥平面;
(2)求二面角平面角的余弦值.
20.已知函数,.
(1)当时,求函数在处的切线方程;(2)讨论函数的单调性;
(3)当函数有两个极值点,,且.证明: .
21.已知为坐标原点,椭圆,其右焦点为,为椭圆(一象限部分)上一点,为中点,,面积为.
(1)求椭圆的方程;
(2)过做圆两条切线,切点分别为,求的值.
22.在直角坐标系中,已知曲线C:(为参数),以坐标原点为极点,以轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线C的普通方程和直线的直角坐标方程;
(2)求曲线C与直线交点的极坐标().
23.已知函数.
(1)当时,解不等式;
(2)若在,使得不等式成立,求实数a的取值范围.
2022届高三年级第三次月考 文数 答案
填空题
13. 14. 15. 16.
解答题
17.
(1)
∵,∴,∵,∴.
(2)设,,则
在中,.
在中:①
在中:②
①+②×2:,综上.
18.
(1)由可得;
由可得;由可得;
所以 列联表如下:
男生 女生 合计
90分钟以上 80 100 180
90分钟以下 80 140 220
合计 160 240 400
,
所以没有95%的把握认为完成作业所需时间在90分钟以上与性别有关.
(2)抽取的9人中,男生:人,女生:人,
至少有一人为男生人数的情况分为:
①男生1人,女生1人;②2人都是男生
所以9人中选择2人共结果有36种.其9人中4个男生记为a.b.c.d.而5个女生记为1.2.3.4.5其中任选2人的结果为
(a,b)(a,c)(a,d)(a,1)(a,2)(a,3)(a,4)(a,5)...8个
(b,c)(b,d)(b,1)(b,2)(b,3)(b,4)(b,5)...7个
... ...
...1个
共8+7+...+1=36
其中1男1女的有5+5+5+5=20个,而2人都是男的有3+2+1=6
所以概率
19.
(1)由,则,
由平面,面,则,
又,,
∴平面,面,
∴,,面,
∴平面 ,面,
∴平面⊥平面.
(2)以为原点,为轴,为轴,为轴建立空间直角坐标系,
∴,,,,
由(1)知:平面,且为的中点,故,又,,
∴平面,则为平面的法向量,即为平面的法向量且,
设平面的法向量为,由,又,
∴,令,则,
设平面与平面所成二面角的大小为,则
20.
解:(Ⅰ)当时,.
∴.
,.
.
∴在处的切线方程.
(Ⅱ)的定义域.
;
①当时,即,
,此时在单调递减;
②当时,即或,
(i)当时,
∴在,单调递减,
在单调递增.
(ii)当时,
∴在单调递减;
综上所述,当时,在单调递减;
当时,在,单调递减,
在单调递增.
(Ⅲ)由(Ⅱ)知,当时,有两个极值点,,且满足:,
由题意知,.
∴
令.
则.
在单调递增,在单调递减.
∴.
即.
21.
(1)设椭圆左焦点为,则,
又,则,
又,
则,
则,
故,
则椭圆方程为.
(2),则,
代入椭圆得,故,,
又过做圆两条切线,切点分别为,
则,
设,,
22.
(1)曲线的参数方程消去参数可得:
故曲线化为普通方程为:,
由,得,
结合
所以直线的直角坐标方程为.
(2)的普通方程可化为,联立,
解得或,
化为极坐标可得,.
23.
(1)当时,.
当时,,解得,结合得;
当时,,解得,结合得;
当时,,解得,结合得.
∴原不等式的解集为.
(2)当时,可化为,
∴或,
即存在,使得,或.
,因为,所以∴,
,因为,所以,所以,
∴实数a的取值范围为.
同课章节目录
