数学：苏科版七上 2.3 数轴

(共23张PPT)
℃
℃
℃
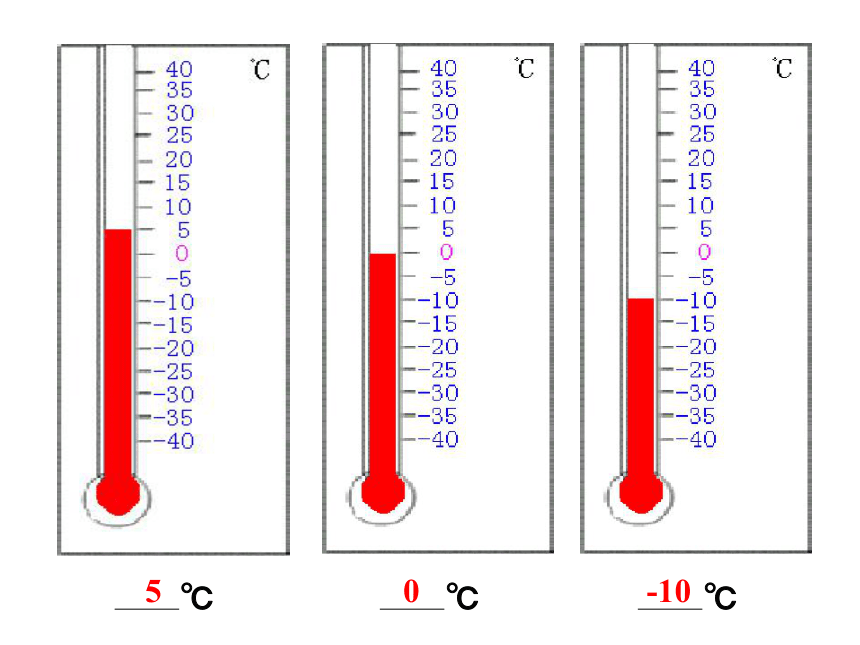
5
0
-10
观察如图的温度计，回答下列问题：
（1）点A表示多少摄氏 度？点B呢？点C呢？
（2）A，B，C三点所表示的温度哪个高？ 哪个低？
温度计上的刻度，使我们能方便地读出温度的度数，直观地判断温度的高低。
那么我们是否也可以用一条直线，画上刻度来表示数呢？
动手操作
1.画一条水平的直线，并在这条直线上任取一点表示0，称为原点。
2.把从原点向右的方向规定为正方向（用箭头表示），向左的方向规定为负方向。
3.取适当的长度（如1cm）为单位长度，在直线上从原点向右每隔一个单位长度取一点，依次表示1，2，3，…。从原点向左每隔一个单位长度取一点，依次表示－1，－2，－3，
…
1.规定了____________________的直线叫做_______
原点、正方向、单位长度
数轴
结论：
原点、正方向、单位长度
2.数轴的三要素是:
温度计就是数轴在生活中的模型
-10
-10
-15
-20
-25
0
-5
5
10
15
25
20
0
1
2
3
4
5
-1
-2
-3
-4
-5
（1）画直线，取原点
（3）统一单位长度，标数
3.画数轴的主要步骤：
（2）标正方向（向右的方向）
强化概念，深入理解
1.下面给出的4条“数轴”，正确的是（ ）
C
强化概念，深入理解
2.下列图形哪些是数轴，哪些不是，为什么？
（A）
（C）
（B）
强化概念，深入理解
（E）
（F）
（D）
例1．如图，指出数轴上点A、B、C表示的数。
点A表示－2
点C表示＋3
点B表示－ —
2
1
解：
0
1
2
-1
-2
-1.5
1|4
4.任何一个有理数都可以用数轴上的一个点来表示,但数轴上的点不都表示有理数。
例2．在数轴上画出表示下列各数的
点：
1|4
+3，-4，
，-1.5
+3
—4
3
-3
-4
练习：在数轴上画出表示下列各数的点 .
（1）2， -1.5, 0, +2.5, ,
（2）100，-50，-25，+50，200，-300
1.填空：
数轴上表示－2的点在原点的 侧，距原点的距离是 ，表示6的点在原点的 侧，距原点的距离是 。
2.判断
⑴数轴上的两个点可以表示同一个有理数 （　）
⑵表示-a的点一定在原点的左边 （ ）
⑶数轴上的所有点都表示有理数 （ ）
⑷ 任何有理数都可以用数轴上的点表示 （ ）
⑸直线就是数轴 （ ）
⑹数轴是一条直线 （ ）
⑺数轴上一个单位长度只能表示1 （ ）
6个单位
左
右
2个单位
X
巩固练习：
X
X
X
√
√
X
3、下列命题正确的是（ ）
A：数轴上表示＋3的点有2个
B：数轴上表示5与-5的点分别在原点的两侧，并且到原点的距离都等于5个单位长度。
C：数轴包括原点与正方向两个要素。
D：数轴上的点只能表示正数和负数。
B
4.填空：
在数轴上，表示数 －2， ,2.6, ,
0 ,-1的点中，在原点左边的点有 个。
5.在数轴上，原点与原点右边的点表示的数是（　）
A、正数　　　　　B、负数　　　　　 C、整数　　　　　D、非负数
2、判断
数轴上的两个点可以表示同一个有理数
（　）
左
左
左
4
D
6.请利用数轴回答下列问题
（1）在数轴上，到原点的距离为6的点有＿＿个，它们表示的数是＿＿＿
（2）在数轴上，从表示2的点出发，先向右移动3个单位长度，再向左移动6个单位长度，最后的终点表示的数是＿＿＿
（3）在数轴上，点M表示数2，那么与点M相距4个单位的点表示的数是＿＿＿＿
2
±6
－1
6或－2
7.点A在数轴上距原点3个单位长度，且位于原点左侧。若将A向右移动4个单位长度，再向左移动1个单位长度，此时A点所表示的是什么数？
8.在数轴上，p点表示2，现在p点向右移动2个单位后，再向左移动10个单位，这时p点必须向 移动 个单位才到达原点。
0
1
2
3
4
5
-1
-2
-3
-4
-5
A1
A2
A
9.如果数轴上点A到原点的距离为3，点B到原点的距离为5，则点A、点B各代表什么数？A、B两点间的距离是多少？
10.一个点在数轴上表示的数是-5，这个点先向左边移动3个单位，然后再向右边移动6个单位，这时它表示的数是多少呢？如果按上面的移动规律，最后得到的点表示的数是2，则开始时它表示什么数？
11.在数轴上点A表示 - 4，如果把原点O向负方向移动1.5个单位，那么在新数轴上点A表示的数是( )
A. B.
C. D.
C
2、判断
数轴上的两个点可以表示同一个有理数
（　）
左
左
左
- 4
我有哪些收获呢？
与大家共分享！
学 而 不 思 则 罔
回头一看，我想说…
归纳小结，强化思想
数轴的概念，数轴的三要素
用数轴上的点表示有理数的方法
任何一个有理数都可以用数轴上的一个点来表示
数轴的引入，使我们能用直观图形来解数的有关概念，这就是“数”与“形”的结合，数形结合是一种重要的方法，我们应注意掌握。
知识象一艘船
让它载着我们
驶向理想的
……
再见！