2021-2022学年人教版数学九年级上册24.1.3 弧、弦、圆心角课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.3 弧、弦、圆心角课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 10:57:14 | ||
图片预览



文档简介
(共19张PPT)
24.1.3 弧、弦、圆心角的关系
圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
追问:旋转任意一个角度呢?
·
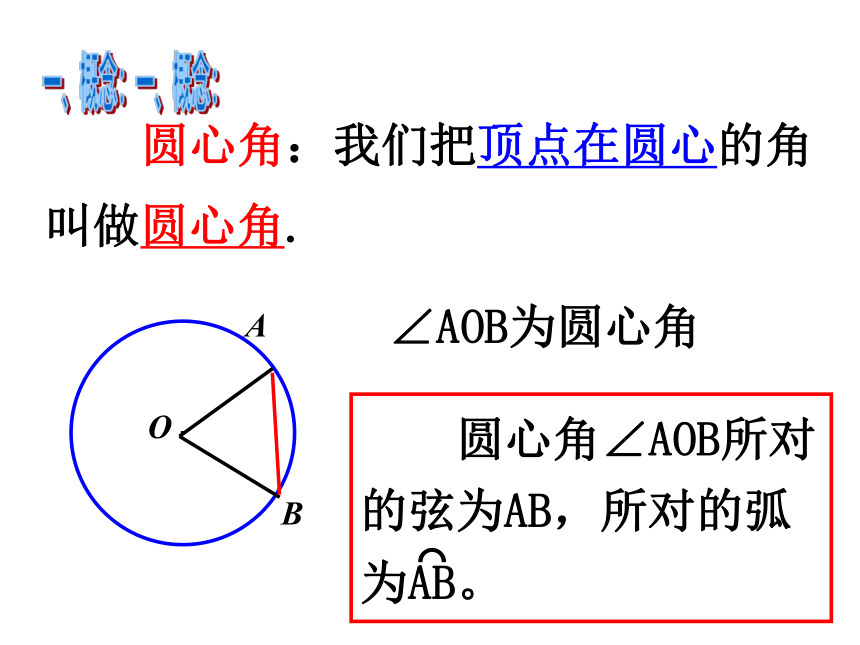
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
一、概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
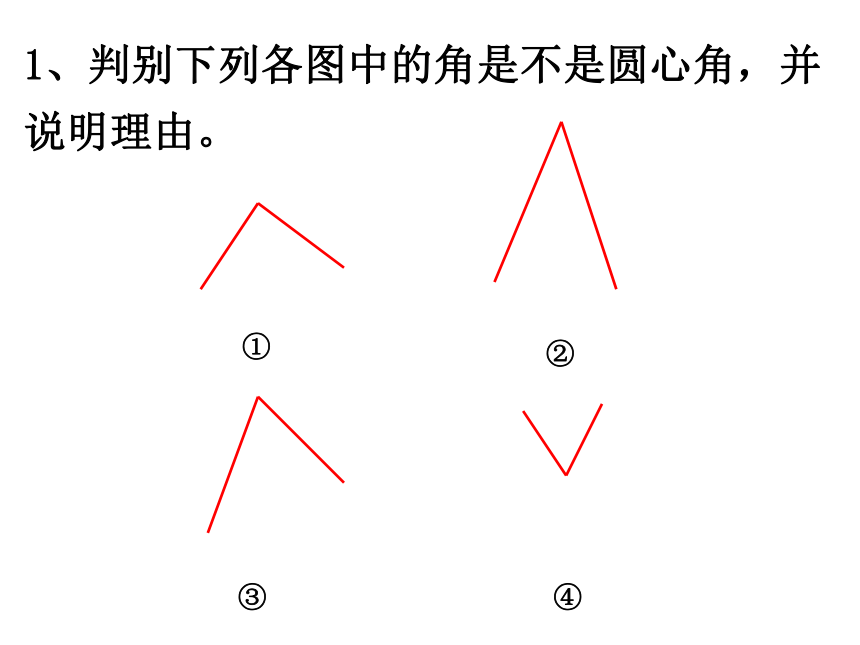
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
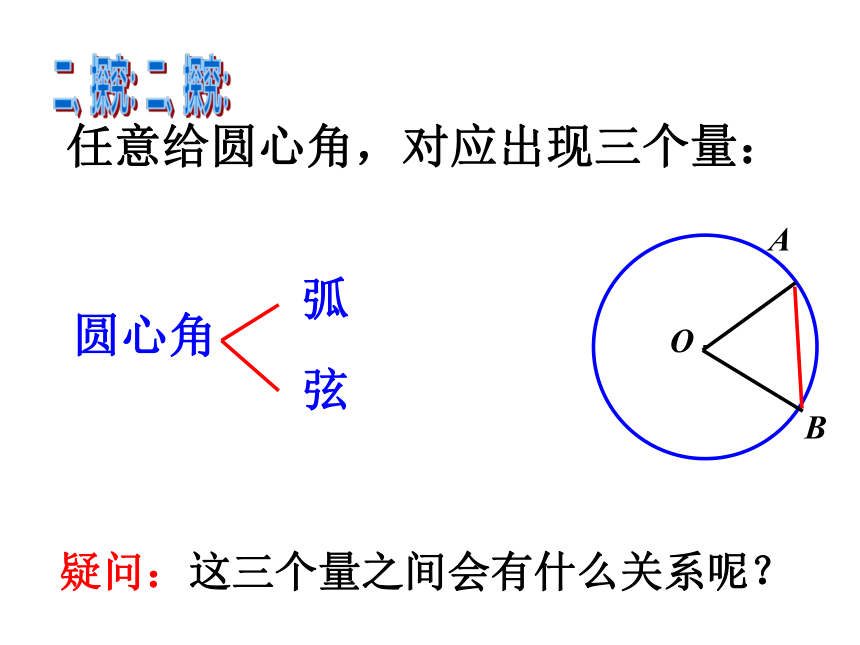
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
二、探究:
疑问:这三个量之间会有什么关系呢?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时, ∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,∴点 A与 A′重合,B与B′重合.
·
O
A
B
·
O
A
B
A′
B′
A′
B′
∴ 重合,AB与A′B′重合.
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
同圆或等圆中,
两个圆心角、两
条弧、两条弦中
有一组量相等,
它们所对应的其
余各组量也相
等.
三、定理:
思考
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
温馨提示:
由弦相等推出弧相等时,
这里弧一般要求
都是优弧或劣弧
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
四、练习:
1.判断下列说法是否正确:
(1)相等的圆心角所对的弧相等。( )
(2)相等的弧所对的弦相等。( )
(3)相等的弦所对的弧相等。( )
×
√
×
小试身手
·
A
B
C
O
例1 如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC
五、例题
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
六、练习:
如图,已知AB、CD为⊙O的两条弦,
AD=BC, 求证AB=CD
⌒ ⌒
七、思考:
如图,已知OA、OB是⊙O的半径,点C为AB的中点,M、N分别为OA、OB的中点,求证:MC=NC
⌒
如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证:AC=AE
⌒ ⌒
4.已知:如图,∠AOB=90°,D、C将
AB三等分,弦AB与半径OD、OC交于点F、E
求证:AE=DC=BF.
⌒
思考 如图,∠AOB=2∠COD,则
AB=2CD吗?
⌒
AB=2CD吗?
⌒
你能总结出规律吗?
想一想:点A是半圆上的三等分点,B是弧NA的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小 并求出AP+BP的最小值.
N
M
B
P
A
O
1、三个元素:
圆心角、弦、弧
八、归纳:
2、三个相等关系:
O
α
A
B
A1
B1
α
(1) 圆心角相等
(2) 弧相等
(3) 弦相等
知一得二
24.1.3 弧、弦、圆心角的关系
圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
追问:旋转任意一个角度呢?
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
一、概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
二、探究:
疑问:这三个量之间会有什么关系呢?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时, ∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,∴点 A与 A′重合,B与B′重合.
·
O
A
B
·
O
A
B
A′
B′
A′
B′
∴ 重合,AB与A′B′重合.
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
同圆或等圆中,
两个圆心角、两
条弧、两条弦中
有一组量相等,
它们所对应的其
余各组量也相
等.
三、定理:
思考
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
温馨提示:
由弦相等推出弧相等时,
这里弧一般要求
都是优弧或劣弧
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
四、练习:
1.判断下列说法是否正确:
(1)相等的圆心角所对的弧相等。( )
(2)相等的弧所对的弦相等。( )
(3)相等的弦所对的弧相等。( )
×
√
×
小试身手
·
A
B
C
O
例1 如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC
五、例题
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
六、练习:
如图,已知AB、CD为⊙O的两条弦,
AD=BC, 求证AB=CD
⌒ ⌒
七、思考:
如图,已知OA、OB是⊙O的半径,点C为AB的中点,M、N分别为OA、OB的中点,求证:MC=NC
⌒
如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证:AC=AE
⌒ ⌒
4.已知:如图,∠AOB=90°,D、C将
AB三等分,弦AB与半径OD、OC交于点F、E
求证:AE=DC=BF.
⌒
思考 如图,∠AOB=2∠COD,则
AB=2CD吗?
⌒
AB=2CD吗?
⌒
你能总结出规律吗?
想一想:点A是半圆上的三等分点,B是弧NA的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小 并求出AP+BP的最小值.
N
M
B
P
A
O
1、三个元素:
圆心角、弦、弧
八、归纳:
2、三个相等关系:
O
α
A
B
A1
B1
α
(1) 圆心角相等
(2) 弧相等
(3) 弦相等
知一得二
同课章节目录
