第十章 静电场中的能量 综合测评卷(A卷)— 高二上学期物理人教版(2019)必修第三册(word版含答案)
文档属性
| 名称 | 第十章 静电场中的能量 综合测评卷(A卷)— 高二上学期物理人教版(2019)必修第三册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 595.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-29 19:24:30 | ||
图片预览




文档简介
第十章 静电场中的能量 综合测评卷(A卷)
一、单选题
1.下面是某同学对电场中的一些概念及公式的理解,其中正确的是( )
A.根据电场强度的定义式可知,电场中某点的电场强度与试探电荷所受的电场力成正比
B.根据电容的定义式可知,电容器的电容与其所带电荷量成正比,与两极板间的电压成反比
C.根据真空中点电荷的场强公式可知,电场中某点的场强与场源电荷所带电荷量成正比
D.根据电势差的定义式可知,如果将一个正点电荷从A点移动到B点,电场力做功为1J,则A、B两点间的电势差为1V
2.如图所示,a、b、c为电场中同一条水平方向电场线上的三点,c为ab的中点,a、b电势分别为φa=5 V、φb=3V。下列叙述正确的是( )
A.该电场在c点处的电势一定为4 V
B.一正电荷从c点运动到b点电势能一定减少
C.a点处的场强Ea一定大于b点处的场强Eb
D.一正电荷运动到c点时受到的静电力由c指向a
3.如图,空间存在一匀强电场(未画出),电场方向与坐标平面平行,以原点为圆心、cm为半径的圆周上任意一点的电势(V),为、两点的连线与轴正方向所成的角,A、、、为圆与坐标轴的交点。关于场强的大小和方向,下列判断正确的是( )
A.场强大小为400 V/m,方向沿轴负方向
B.场强大小为,方向沿轴负方向
C.场强大小为400 V/m,方向沿轴正方向
D.场强大小为,方向沿轴正方向
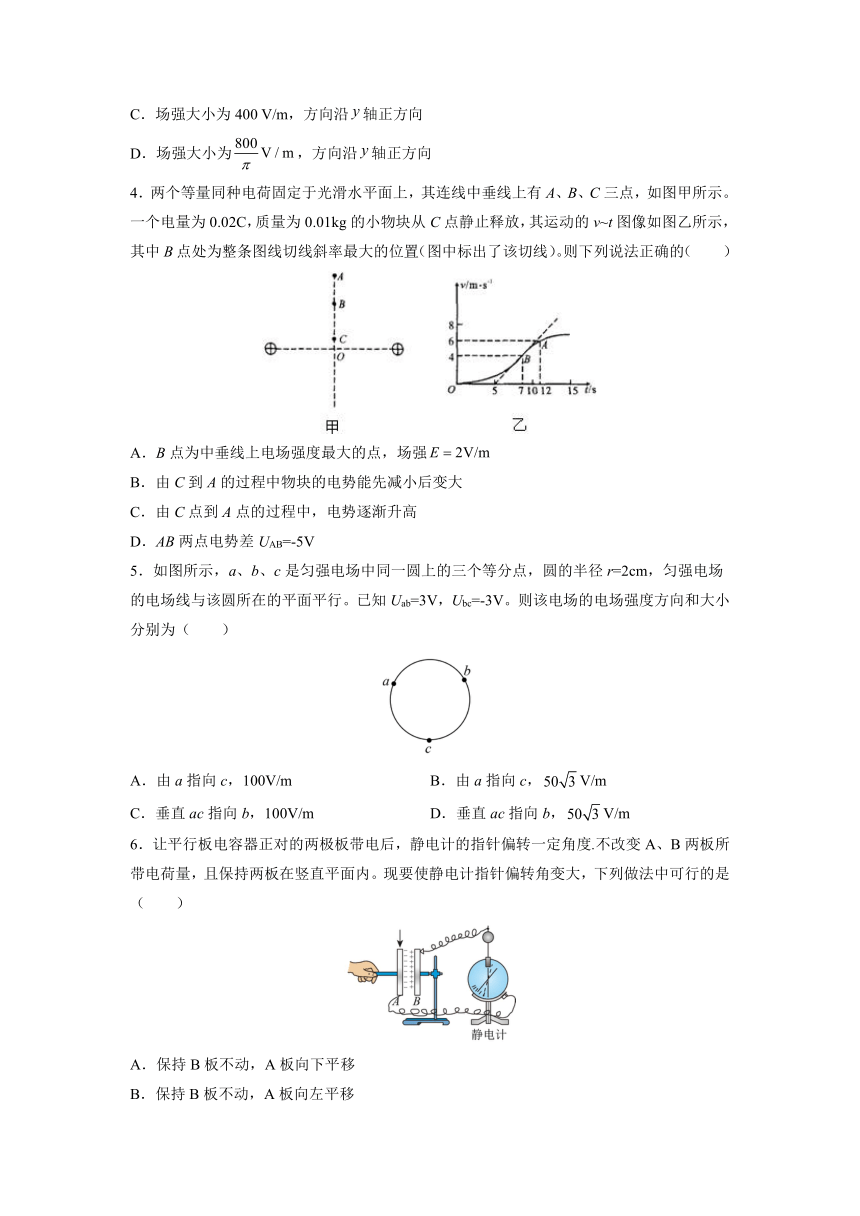
4.两个等量同种电荷固定于光滑水平面上,其连线中垂线上有A、B、C三点,如图甲所示。一个电量为0.02C,质量为0.01kg的小物块从C点静止释放,其运动的v~t图像如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线)。则下列说法正确的( )
A.B点为中垂线上电场强度最大的点,场强
B.由C到A的过程中物块的电势能先减小后变大
C.由C点到A点的过程中,电势逐渐升高
D.AB两点电势差UAB=-5V
5.如图所示,a、b、c是匀强电场中同一圆上的三个等分点,圆的半径r=2cm,匀强电场的电场线与该圆所在的平面平行。已知Uab=3V,Ubc=-3V。则该电场的电场强度方向和大小分别为( )
A.由a指向c,100V/m B.由a指向c,V/m
C.垂直ac指向b,100V/m D.垂直ac指向b,V/m
6.让平行板电容器正对的两极板带电后,静电计的指针偏转一定角度.不改变A、B两板所带电荷量,且保持两板在竖直平面内。现要使静电计指针偏转角变大,下列做法中可行的是 ( )
A.保持B板不动,A板向下平移
B.保持B板不动,A板向左平移
C.保持B板不动,A板向右平移
D.保持A、B两板不动,在A、B之间插入一块绝缘介质板
7.如图所示的同心圆(虚线)是电场中的一簇等势线,一个正电子只在电场力作用下沿着直线由A向C运动时的速度越来越小,B为线段的中点,则有( )
A.正电子沿运动时受到的电场力越来越小
B.正电子沿运动时它具有的电势能越来越小
C.电势
D.电势差
8.如图所示,A为粒子源,A和极板B间的加速电压为U1,两水平放置的平行带电板C、D间的电压为U2。现有质量为m、电荷量为+q的粒子从A处由静止释放,被加速电压U1加速后水平进入竖直方向的匀强电场,最后从右侧射出。平行板C、D的长度为L,两板间的距离为d,不计带电粒子的重力,则下列说法正确的是( )
A.带电粒子射出B板时的速度v0=
B.带电粒子在C、D极板间运动的时间t=L
C.带电粒子飞出C、D间电场时在竖直方向上发生的位移y=
D.若同时使U1和U2加倍,则带电粒子在飞出C、D极板间的电场时的速度与水平方向的夹角将加倍
二、多选题
9.所示,一个电荷量为的点电荷甲,固定在绝缘水平面上的O点。另一个电荷量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时速度为v,且为运动过程中速度的最小值。已知点电荷乙受到的阻力大小恒为f,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
A.点电荷乙从A点向甲运动的过程中,加速度逐渐增大
B.点电荷乙从A点向甲运动的过程中,其电势能一直减小
C.OB间的距离为
D.在点电荷甲形成的电场中,AB间电势差
10.图中的实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,下列说法正确的是( )
A.粒子在M点受到的电场力大于在N点受到的电场力
B.粒子在M点的加速度小于在N点的加速度
C.粒子在M点的速度小于在N点的速度
D.粒子从M点到N点做的是变加速运动
11.我国成功研制了“3.0V 12000F”石墨烯超级电容器。超级电容器充电时,电极表面将吸引周围电解质溶液中的异性离子,使这些离子附着于电极表面上形成相距小于0.5nm、相互绝缘的等量异种电荷层,石墨烯电极结构使得该异种电荷层的面积成万倍增加。下列有关说法正确的是( )
A.该电容器充满电后的带电荷量为36000C
B.该电容器充满电后的带电荷量为72000C
C.电介质相同时,正对面积大、板间距离小,则电容大
D.当该电容器放电至两端电压为1.5V时,其电容变为6000F
12.如图所示,空间有一匀强电场,电场方向与纸面平行。一电荷量为-q的粒子(重力不计),在恒力F的作用下沿虚线由M匀速运动到N。已知力F和MN间夹角为θ,M、N间距离为d,则下列结论中正确的是( )
A.M、N两点的电势差为
B.匀强电场的电场强度大小为
C.带电粒子由M运动到N的过程中,电势能增加了Fdcosθ
D.若要使带电粒子由N向M做匀速直线运动,则F必须反向
三、解答题
13.竖直方向上无限大均匀带电平板上有一小孔,平板右侧过点且垂直于板的轴上的电势随距离的变化如图所示。一个电荷量,质量的带电粒子从点以初速度沿轴正方向运动,忽略粒子重力。
(1)求粒子在处所受的电场力;
(2)请通过计算说明粒子能否到达处。若能,求出粒子到达该处的速度大小;若不能,求出粒子向右运动最远点的位置坐标。
14.如图所示,虚线左侧有一场强为的匀强电场,在两条平行的虚线和之间存在着宽为、电场强度为的匀强电场,在虚线右侧距为处有一与电场平行的屏。现将一电子(电荷量为,质量为,重力不计)无初速度地放入电场中的点,最后电子打在右侧的屏上,点到的距离为,连线与屏垂直,垂足为,求:
(1)电子到的速度大小;
(2)电子从释放到打到屏上所用的时间;
(3)电子刚射出电场时的速度方向与连线夹角的正切值;
(4)电子打到屏上的点到点的距离。
15.在光滑绝缘水平面上放置一质量m=0.2kg、电荷量的小球,小球系在长L=0.5m的绝缘细线上,线的另一端固定在O点。整个装置放置于的匀强电场中,电场方向与水平面平行且沿OA方向,如图所示(此图为俯视图)。现给小球一垂直于细线的初速度使其从A点开始绕O点做圆周运动,小球可视为质点。求:
(1)小球运动过程中绳子拉力的最大值;
(2)若小球运动到动能最小的位置时细线被剪断,则小球经过多长时间其动能变为最小动能的2倍?
(3)当某次小球运动到A点时,电场方向突然反向但场强大小不变,并且此后小球每转过,场强均反向且场强大小不变,求:
①小球每次刚好到达A处时,细线承受的张力记为,求的表达式;
②若细线最大张力足够,从电场第一次反向开始,小球转过角度满足时,求绳子张力关于的表达式。
16.一束初速不计的一价正离子在经的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离,板长,两个极板上电压为,已知,粒子的质量为。(重力忽略不计)求:
(1)粒子进入偏转电场时的速度;
(2)粒子在偏转电场中的加速度;
(3)粒子飞出平行板时的侧移量;
(4)粒子出场时的速度;
(5)偏转场对粒子做的功。
17.如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成角的绝缘直杆,其下端(端)距地面高度。有一质量的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过端的正下方点处。(取)求:
(1)小环离开直杆后的加速度大小和方向;
(2)小环从运动到过程中的动能增量;
(3)小环在直杆上匀速运动速度的大小。
参考答案
1.C
【解析】A. 电场强度由电场本身决定,与试探电荷受到的电场力和电荷量都无关,选项A错误;
B. 电容器的电容由电容器本身结构决定,与电容器所带的电荷量和两板之间的电压无关,选项B错误;
C. 公式是真空中点电荷产生场强的决定式,即电场中某点的场强与场源电荷所带电荷量成正比,与该点到场源电荷的距离的平方成反比,选项C正确;
D. 根据电势差的定义式可知,如果将一个电荷量为1C的正点电荷从A点移动到B点,电场力做功为1J,则A、B两点间的电势差为1V,即表述中少了“电荷量为1C” 的条件,选项D错误。
故选C。
2.B
【解析】A.当该电场是匀强电场时,由于沿电场方向相同距离电势差相等,则场在c点处的电势一定为4V,当该电场不是匀强电场时,在c点处的电势不一定为4V,故A错误;
BD.由题可判断电场线方向从a指向b,正电荷运动到c点时受到的电场力由a指向c,根据沿着电场线方向电势降低可知c点的电势高于b点的电势,根据正电荷在电势高处电势能大可知,正电荷从c点运动到b点电势能一定减少,故B正确,D错误;
C.一条电场线无法比较电场线的疏密,就无法比较场强的大小,则a点处的场强不一定大于b点处的场强,故C错误。
故选B。
3.A
【解析】由题意可知,在圆与坐标轴的四个交点处的电势分别为
、、、
由于
即、处于同一等势面上,可知电场线与、的连线垂直,根据匀强电场的场强与电势差的关系,有
方向沿轴负方向,故A正确,BCD错误。
故选A。
4.D
【解析】A.v~t图像中图线的斜率表示加速度,图像的斜率为
由牛顿第二定律可得
B点处为整条图线切线斜率最大的位置,因此B点为中垂线上电场强度最大的点,场强大小为
A错误;
B.由C到A的过程中物块的速度逐渐增大,则物块的动能逐渐增大,由能量守恒定律可得,物块的电势能逐渐减小,B错误;
C.沿着电场线方向电势逐渐降低,由等量同种电荷电场线分布规律可得,由C点到A点的过程中,电势逐渐降低,C错误;
D.由B点到A点的过程中,由动能定理可得
解得
因此
D正确;
故选D。
5.C
【解析】由题给信息Uab=3V,Ubc=-3V知a、c两点电势相等,处在同一等势面上,根据电场强度方向与等势面垂直,指向电势降低的方向,可知该电场的电场强度方向垂直ac指向b,如图:
则电场强度的大小
故选C。
6.AB
【解析】A.保持B板不动,A板向上平移,减小两极板的正对面积S时,由电容的决定式C=分析可知电容C减小,而电容器的电荷量Q不变,则由C=得到,板间电压U增大,静电计的指针偏角变大,故A正确;
B.保持B板不动,A板向左平移,使两极板远离一些时,板间距离d增大,由电容的决定式C=,分析可知电容C减小,而电容器的电量Q不变,则由C=得到,板间电压U增大,静电计的指针偏角变大,故B正确;
C.保持B板不动,A板向右平移,使两极板靠近一些时,板间距离d减小,由电容的决定式C=,分析可知电容C增大,而电容器的电荷量Q不变,则由C=得到,板间电压U减小,静电计的指针偏角变小,故C错误;
D.保持A、B两板不动,在两极板间插入一块绝缘介质板时,由电容的决定式C=,分析可知电容C增大,而电容器的电荷量Q不变,则由C=得到,板间电压U减小,静电计的指针偏角变小,故D错误。
故选AB。
7.C
【解析】A.由于等势线是电场中的一簇同心圆,且正电子由A向C运动中速度越来越小,因此题中电场由处于圆心的正电荷产生的,由库仑定律可知,正电子沿着直线由A向C运动时受到电场力越来越大,A错误;
B.正电子沿运动时,速度越来越小,电场力做负功,则它具有的电势能越来越大,B错误;
C.电场线与等势面垂直,且由电势高的等势线指向电势低的等势线,正电子由A向C运动时的速度越来越小,则电场力向外,场强方向向外,因此内侧电势高,φA<φB<φC,C正确;
D.电子沿AC方向运动中,电场力逐渐变大,从A到B电场力较小,因此从A到B运动中电场力做功较少,由,可知
UABD错误。
故选C。
8.A
【解析】A.粒子从粒子源A到B板由动能定理得
故
故A正确;
B.粒子在C、D间的运动时间
故B错误;
C.粒子飞出C、D间时在竖直方向发生的位移
故C错误;
D.若粒子飞出C、D极板间时速度与水平方向夹角为θ,则
同时使U1和U2加倍,夹角不变,故D错误。
故选A。
9.BCD
【解析】A.点电荷乙从A点向甲运动的过程中,受向左的库伦力和向右的摩擦力,两球靠近过程中库仑力逐渐增大,由题意知小球先减速后加速,所以加速度先减小后增大,故A错误;
B.点电荷乙向左运动的过程中,电场力一直做正功,所以其电势能一直减小,故B正确;
C.当速度最小时有
解得OB间的距离为
故C正确;
D.点电荷从A运动到B的过程中,根据动能定理有
解得
故D正确。
故选BCD。
10.BCD
【解析】AB.从题图中可以看出,M点处的电场线较疏,而N点处的电场线较密,所以粒子在M点所受的电场力要小于在N点所受的电场力,则粒子在M点的加速度小于在N点的加速度,故B正确,A错误;
C.因粒子只受电场力作用,由题图可以看出,电场力对其做正功,所以粒子的动能增加,速度增大,故C正确;
D.由于粒子在运动过程中受到的电场力是个变力,所以粒子所做的运动是变加速运动,故D正确。
故选BCD。
11.AC
【解析】A.B根据超级电容器的规格“3.0V 12000F”,结合
可知该电容器充满电后的带电荷量
故A正确,B错误;
C.借助平行板电容器电容的决定式
分析可知,电介质相同时,正对面积大,板间距离小,则电容大,故C正确;
D.电容器的电容只与电容器本身有关,与电容器所带电荷量和两极板间电压无关,故D错误。
故选AC。
12.BC
【解析】A.粒子做匀速运动,根据动能定理,有
可得
故A错误;
B.粒子做匀速运动,受力平衡,则电场强度大小
故B正确;
C.粒子做匀速运动,F做正功,由A的分析可知,电场力做负功,所以电势能的增加量等于克服电场力做的功Fdcos θ,故C正确;
D.粒子做匀速直线运动的条件是粒子受力平衡,即由N运动到M,受力不变,故D错误。
故选BC。
13.(1),方向水平指向点;(2)不能到达,
【解析】解:(1)由电势分布图像可知,此电场为匀强电场
场强大小
故粒子运动到处所受电场力
方向水平指向点
(2)假设粒子运动距点的最大距离为,由动能定理得
故粒子不能到达处,粒子向右运动最远点的位置坐标为
14.(1) ;(2);(3) ;(4)
【解析】(1)电子从A运动到MN的过程中,根据动能定理得
解得
(2)电子在电场E1中做初速度为零的匀加速直线运动,设加速度为a1,时间为t1,则
由,得
从MN到屏的过程中运动时间
运动的总时间
(3) 设粒子射出电场E2时平行电场方向的速度为vy,由牛顿第二定律得:电子进入电场E2时的加速度为
电子在电场E2中运动时间
则
电子刚射出电场E2时的速度方向与AO连线夹角的正切值为
解得
(4)带电粒子在电场中的运动轨迹如图所示
设电子打到屏上的点到O点的距离x,根据上图有几何关系得
解得
15.(1);(2);(3)①;②
【解析】(1)小球在A点时细线的拉力最大,对其进行受力分析,
由牛顿第二定律可得
解得
(2)小球运动到B处时,电势能最大,动能最小。设小球到达B处时速度为,
从A运动到B,由动能定理得
解得
,,
设经过时间后其动能变为最小动能的2倍。设小球沿BA方向移动的距离为,
则由动能定理得
由类平抛运动可知
解得
(3)①小球运动到A点时速度仍为,此后由于电场反向,运动到B的过程中,电场力做正功。到B处后电场又反向,电场力总是做正功。设电场反向后小球第n次到达A处时速度为,
由动能定理得
刚好到达A处时,对其进行受力分析,由牛顿第二定律得
解得
②当小球转过后,速度为,由动能定理得
对其进行受力分析,由牛顿第二定律得
解得
16.(1);(2);(3);(4);(5)
【解析】(1)粒子加速过程中,由动能定理可得
代入数据,可得
(2)根据牛顿第二定律,可得粒子在偏转电场中的加速度
代入数据,可得
(3)粒子沿初速度方向做匀速直线运动,在偏转电场中的飞行时间设为t,则有
代入数据,可得
粒子飞出平行板时的侧移量
联立,可得
(4)粒子出场时的速度设为v,可以分解为沿初速度方向的v0和沿电场方向的vy,其中
根据勾股定理,可得
(5)根据恒力功的定义式,可得偏转场对粒子做的功为
代入数据,可得
17.(1),加速度方向垂直杆向下;(2)4J;(3)
【解析】(1)小环沿杆匀速下滑,受重力,电场力及支持力如图所示,由平衡条件可得
,
小环离开直杆后,只受重力及电场力作用,小环的加速度为
解得
, 加速度方向垂直杆向下
(2)小环从运动到过程中,由动能定理可得
解得
(3)小环从运动到过程中,做类平抛运动,如图所示有
代入数据联立解得
一、单选题
1.下面是某同学对电场中的一些概念及公式的理解,其中正确的是( )
A.根据电场强度的定义式可知,电场中某点的电场强度与试探电荷所受的电场力成正比
B.根据电容的定义式可知,电容器的电容与其所带电荷量成正比,与两极板间的电压成反比
C.根据真空中点电荷的场强公式可知,电场中某点的场强与场源电荷所带电荷量成正比
D.根据电势差的定义式可知,如果将一个正点电荷从A点移动到B点,电场力做功为1J,则A、B两点间的电势差为1V
2.如图所示,a、b、c为电场中同一条水平方向电场线上的三点,c为ab的中点,a、b电势分别为φa=5 V、φb=3V。下列叙述正确的是( )
A.该电场在c点处的电势一定为4 V
B.一正电荷从c点运动到b点电势能一定减少
C.a点处的场强Ea一定大于b点处的场强Eb
D.一正电荷运动到c点时受到的静电力由c指向a
3.如图,空间存在一匀强电场(未画出),电场方向与坐标平面平行,以原点为圆心、cm为半径的圆周上任意一点的电势(V),为、两点的连线与轴正方向所成的角,A、、、为圆与坐标轴的交点。关于场强的大小和方向,下列判断正确的是( )
A.场强大小为400 V/m,方向沿轴负方向
B.场强大小为,方向沿轴负方向
C.场强大小为400 V/m,方向沿轴正方向
D.场强大小为,方向沿轴正方向
4.两个等量同种电荷固定于光滑水平面上,其连线中垂线上有A、B、C三点,如图甲所示。一个电量为0.02C,质量为0.01kg的小物块从C点静止释放,其运动的v~t图像如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线)。则下列说法正确的( )
A.B点为中垂线上电场强度最大的点,场强
B.由C到A的过程中物块的电势能先减小后变大
C.由C点到A点的过程中,电势逐渐升高
D.AB两点电势差UAB=-5V
5.如图所示,a、b、c是匀强电场中同一圆上的三个等分点,圆的半径r=2cm,匀强电场的电场线与该圆所在的平面平行。已知Uab=3V,Ubc=-3V。则该电场的电场强度方向和大小分别为( )
A.由a指向c,100V/m B.由a指向c,V/m
C.垂直ac指向b,100V/m D.垂直ac指向b,V/m
6.让平行板电容器正对的两极板带电后,静电计的指针偏转一定角度.不改变A、B两板所带电荷量,且保持两板在竖直平面内。现要使静电计指针偏转角变大,下列做法中可行的是 ( )
A.保持B板不动,A板向下平移
B.保持B板不动,A板向左平移
C.保持B板不动,A板向右平移
D.保持A、B两板不动,在A、B之间插入一块绝缘介质板
7.如图所示的同心圆(虚线)是电场中的一簇等势线,一个正电子只在电场力作用下沿着直线由A向C运动时的速度越来越小,B为线段的中点,则有( )
A.正电子沿运动时受到的电场力越来越小
B.正电子沿运动时它具有的电势能越来越小
C.电势
D.电势差
8.如图所示,A为粒子源,A和极板B间的加速电压为U1,两水平放置的平行带电板C、D间的电压为U2。现有质量为m、电荷量为+q的粒子从A处由静止释放,被加速电压U1加速后水平进入竖直方向的匀强电场,最后从右侧射出。平行板C、D的长度为L,两板间的距离为d,不计带电粒子的重力,则下列说法正确的是( )
A.带电粒子射出B板时的速度v0=
B.带电粒子在C、D极板间运动的时间t=L
C.带电粒子飞出C、D间电场时在竖直方向上发生的位移y=
D.若同时使U1和U2加倍,则带电粒子在飞出C、D极板间的电场时的速度与水平方向的夹角将加倍
二、多选题
9.所示,一个电荷量为的点电荷甲,固定在绝缘水平面上的O点。另一个电荷量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时速度为v,且为运动过程中速度的最小值。已知点电荷乙受到的阻力大小恒为f,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
A.点电荷乙从A点向甲运动的过程中,加速度逐渐增大
B.点电荷乙从A点向甲运动的过程中,其电势能一直减小
C.OB间的距离为
D.在点电荷甲形成的电场中,AB间电势差
10.图中的实线表示电场线,虚线表示只受电场力作用的带正电粒子的运动轨迹,粒子先经过M点,再经过N点,下列说法正确的是( )
A.粒子在M点受到的电场力大于在N点受到的电场力
B.粒子在M点的加速度小于在N点的加速度
C.粒子在M点的速度小于在N点的速度
D.粒子从M点到N点做的是变加速运动
11.我国成功研制了“3.0V 12000F”石墨烯超级电容器。超级电容器充电时,电极表面将吸引周围电解质溶液中的异性离子,使这些离子附着于电极表面上形成相距小于0.5nm、相互绝缘的等量异种电荷层,石墨烯电极结构使得该异种电荷层的面积成万倍增加。下列有关说法正确的是( )
A.该电容器充满电后的带电荷量为36000C
B.该电容器充满电后的带电荷量为72000C
C.电介质相同时,正对面积大、板间距离小,则电容大
D.当该电容器放电至两端电压为1.5V时,其电容变为6000F
12.如图所示,空间有一匀强电场,电场方向与纸面平行。一电荷量为-q的粒子(重力不计),在恒力F的作用下沿虚线由M匀速运动到N。已知力F和MN间夹角为θ,M、N间距离为d,则下列结论中正确的是( )
A.M、N两点的电势差为
B.匀强电场的电场强度大小为
C.带电粒子由M运动到N的过程中,电势能增加了Fdcosθ
D.若要使带电粒子由N向M做匀速直线运动,则F必须反向
三、解答题
13.竖直方向上无限大均匀带电平板上有一小孔,平板右侧过点且垂直于板的轴上的电势随距离的变化如图所示。一个电荷量,质量的带电粒子从点以初速度沿轴正方向运动,忽略粒子重力。
(1)求粒子在处所受的电场力;
(2)请通过计算说明粒子能否到达处。若能,求出粒子到达该处的速度大小;若不能,求出粒子向右运动最远点的位置坐标。
14.如图所示,虚线左侧有一场强为的匀强电场,在两条平行的虚线和之间存在着宽为、电场强度为的匀强电场,在虚线右侧距为处有一与电场平行的屏。现将一电子(电荷量为,质量为,重力不计)无初速度地放入电场中的点,最后电子打在右侧的屏上,点到的距离为,连线与屏垂直,垂足为,求:
(1)电子到的速度大小;
(2)电子从释放到打到屏上所用的时间;
(3)电子刚射出电场时的速度方向与连线夹角的正切值;
(4)电子打到屏上的点到点的距离。
15.在光滑绝缘水平面上放置一质量m=0.2kg、电荷量的小球,小球系在长L=0.5m的绝缘细线上,线的另一端固定在O点。整个装置放置于的匀强电场中,电场方向与水平面平行且沿OA方向,如图所示(此图为俯视图)。现给小球一垂直于细线的初速度使其从A点开始绕O点做圆周运动,小球可视为质点。求:
(1)小球运动过程中绳子拉力的最大值;
(2)若小球运动到动能最小的位置时细线被剪断,则小球经过多长时间其动能变为最小动能的2倍?
(3)当某次小球运动到A点时,电场方向突然反向但场强大小不变,并且此后小球每转过,场强均反向且场强大小不变,求:
①小球每次刚好到达A处时,细线承受的张力记为,求的表达式;
②若细线最大张力足够,从电场第一次反向开始,小球转过角度满足时,求绳子张力关于的表达式。
16.一束初速不计的一价正离子在经的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离,板长,两个极板上电压为,已知,粒子的质量为。(重力忽略不计)求:
(1)粒子进入偏转电场时的速度;
(2)粒子在偏转电场中的加速度;
(3)粒子飞出平行板时的侧移量;
(4)粒子出场时的速度;
(5)偏转场对粒子做的功。
17.如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成角的绝缘直杆,其下端(端)距地面高度。有一质量的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过端的正下方点处。(取)求:
(1)小环离开直杆后的加速度大小和方向;
(2)小环从运动到过程中的动能增量;
(3)小环在直杆上匀速运动速度的大小。
参考答案
1.C
【解析】A. 电场强度由电场本身决定,与试探电荷受到的电场力和电荷量都无关,选项A错误;
B. 电容器的电容由电容器本身结构决定,与电容器所带的电荷量和两板之间的电压无关,选项B错误;
C. 公式是真空中点电荷产生场强的决定式,即电场中某点的场强与场源电荷所带电荷量成正比,与该点到场源电荷的距离的平方成反比,选项C正确;
D. 根据电势差的定义式可知,如果将一个电荷量为1C的正点电荷从A点移动到B点,电场力做功为1J,则A、B两点间的电势差为1V,即表述中少了“电荷量为1C” 的条件,选项D错误。
故选C。
2.B
【解析】A.当该电场是匀强电场时,由于沿电场方向相同距离电势差相等,则场在c点处的电势一定为4V,当该电场不是匀强电场时,在c点处的电势不一定为4V,故A错误;
BD.由题可判断电场线方向从a指向b,正电荷运动到c点时受到的电场力由a指向c,根据沿着电场线方向电势降低可知c点的电势高于b点的电势,根据正电荷在电势高处电势能大可知,正电荷从c点运动到b点电势能一定减少,故B正确,D错误;
C.一条电场线无法比较电场线的疏密,就无法比较场强的大小,则a点处的场强不一定大于b点处的场强,故C错误。
故选B。
3.A
【解析】由题意可知,在圆与坐标轴的四个交点处的电势分别为
、、、
由于
即、处于同一等势面上,可知电场线与、的连线垂直,根据匀强电场的场强与电势差的关系,有
方向沿轴负方向,故A正确,BCD错误。
故选A。
4.D
【解析】A.v~t图像中图线的斜率表示加速度,图像的斜率为
由牛顿第二定律可得
B点处为整条图线切线斜率最大的位置,因此B点为中垂线上电场强度最大的点,场强大小为
A错误;
B.由C到A的过程中物块的速度逐渐增大,则物块的动能逐渐增大,由能量守恒定律可得,物块的电势能逐渐减小,B错误;
C.沿着电场线方向电势逐渐降低,由等量同种电荷电场线分布规律可得,由C点到A点的过程中,电势逐渐降低,C错误;
D.由B点到A点的过程中,由动能定理可得
解得
因此
D正确;
故选D。
5.C
【解析】由题给信息Uab=3V,Ubc=-3V知a、c两点电势相等,处在同一等势面上,根据电场强度方向与等势面垂直,指向电势降低的方向,可知该电场的电场强度方向垂直ac指向b,如图:
则电场强度的大小
故选C。
6.AB
【解析】A.保持B板不动,A板向上平移,减小两极板的正对面积S时,由电容的决定式C=分析可知电容C减小,而电容器的电荷量Q不变,则由C=得到,板间电压U增大,静电计的指针偏角变大,故A正确;
B.保持B板不动,A板向左平移,使两极板远离一些时,板间距离d增大,由电容的决定式C=,分析可知电容C减小,而电容器的电量Q不变,则由C=得到,板间电压U增大,静电计的指针偏角变大,故B正确;
C.保持B板不动,A板向右平移,使两极板靠近一些时,板间距离d减小,由电容的决定式C=,分析可知电容C增大,而电容器的电荷量Q不变,则由C=得到,板间电压U减小,静电计的指针偏角变小,故C错误;
D.保持A、B两板不动,在两极板间插入一块绝缘介质板时,由电容的决定式C=,分析可知电容C增大,而电容器的电荷量Q不变,则由C=得到,板间电压U减小,静电计的指针偏角变小,故D错误。
故选AB。
7.C
【解析】A.由于等势线是电场中的一簇同心圆,且正电子由A向C运动中速度越来越小,因此题中电场由处于圆心的正电荷产生的,由库仑定律可知,正电子沿着直线由A向C运动时受到电场力越来越大,A错误;
B.正电子沿运动时,速度越来越小,电场力做负功,则它具有的电势能越来越大,B错误;
C.电场线与等势面垂直,且由电势高的等势线指向电势低的等势线,正电子由A向C运动时的速度越来越小,则电场力向外,场强方向向外,因此内侧电势高,φA<φB<φC,C正确;
D.电子沿AC方向运动中,电场力逐渐变大,从A到B电场力较小,因此从A到B运动中电场力做功较少,由,可知
UAB
故选C。
8.A
【解析】A.粒子从粒子源A到B板由动能定理得
故
故A正确;
B.粒子在C、D间的运动时间
故B错误;
C.粒子飞出C、D间时在竖直方向发生的位移
故C错误;
D.若粒子飞出C、D极板间时速度与水平方向夹角为θ,则
同时使U1和U2加倍,夹角不变,故D错误。
故选A。
9.BCD
【解析】A.点电荷乙从A点向甲运动的过程中,受向左的库伦力和向右的摩擦力,两球靠近过程中库仑力逐渐增大,由题意知小球先减速后加速,所以加速度先减小后增大,故A错误;
B.点电荷乙向左运动的过程中,电场力一直做正功,所以其电势能一直减小,故B正确;
C.当速度最小时有
解得OB间的距离为
故C正确;
D.点电荷从A运动到B的过程中,根据动能定理有
解得
故D正确。
故选BCD。
10.BCD
【解析】AB.从题图中可以看出,M点处的电场线较疏,而N点处的电场线较密,所以粒子在M点所受的电场力要小于在N点所受的电场力,则粒子在M点的加速度小于在N点的加速度,故B正确,A错误;
C.因粒子只受电场力作用,由题图可以看出,电场力对其做正功,所以粒子的动能增加,速度增大,故C正确;
D.由于粒子在运动过程中受到的电场力是个变力,所以粒子所做的运动是变加速运动,故D正确。
故选BCD。
11.AC
【解析】A.B根据超级电容器的规格“3.0V 12000F”,结合
可知该电容器充满电后的带电荷量
故A正确,B错误;
C.借助平行板电容器电容的决定式
分析可知,电介质相同时,正对面积大,板间距离小,则电容大,故C正确;
D.电容器的电容只与电容器本身有关,与电容器所带电荷量和两极板间电压无关,故D错误。
故选AC。
12.BC
【解析】A.粒子做匀速运动,根据动能定理,有
可得
故A错误;
B.粒子做匀速运动,受力平衡,则电场强度大小
故B正确;
C.粒子做匀速运动,F做正功,由A的分析可知,电场力做负功,所以电势能的增加量等于克服电场力做的功Fdcos θ,故C正确;
D.粒子做匀速直线运动的条件是粒子受力平衡,即由N运动到M,受力不变,故D错误。
故选BC。
13.(1),方向水平指向点;(2)不能到达,
【解析】解:(1)由电势分布图像可知,此电场为匀强电场
场强大小
故粒子运动到处所受电场力
方向水平指向点
(2)假设粒子运动距点的最大距离为,由动能定理得
故粒子不能到达处,粒子向右运动最远点的位置坐标为
14.(1) ;(2);(3) ;(4)
【解析】(1)电子从A运动到MN的过程中,根据动能定理得
解得
(2)电子在电场E1中做初速度为零的匀加速直线运动,设加速度为a1,时间为t1,则
由,得
从MN到屏的过程中运动时间
运动的总时间
(3) 设粒子射出电场E2时平行电场方向的速度为vy,由牛顿第二定律得:电子进入电场E2时的加速度为
电子在电场E2中运动时间
则
电子刚射出电场E2时的速度方向与AO连线夹角的正切值为
解得
(4)带电粒子在电场中的运动轨迹如图所示
设电子打到屏上的点到O点的距离x,根据上图有几何关系得
解得
15.(1);(2);(3)①;②
【解析】(1)小球在A点时细线的拉力最大,对其进行受力分析,
由牛顿第二定律可得
解得
(2)小球运动到B处时,电势能最大,动能最小。设小球到达B处时速度为,
从A运动到B,由动能定理得
解得
,,
设经过时间后其动能变为最小动能的2倍。设小球沿BA方向移动的距离为,
则由动能定理得
由类平抛运动可知
解得
(3)①小球运动到A点时速度仍为,此后由于电场反向,运动到B的过程中,电场力做正功。到B处后电场又反向,电场力总是做正功。设电场反向后小球第n次到达A处时速度为,
由动能定理得
刚好到达A处时,对其进行受力分析,由牛顿第二定律得
解得
②当小球转过后,速度为,由动能定理得
对其进行受力分析,由牛顿第二定律得
解得
16.(1);(2);(3);(4);(5)
【解析】(1)粒子加速过程中,由动能定理可得
代入数据,可得
(2)根据牛顿第二定律,可得粒子在偏转电场中的加速度
代入数据,可得
(3)粒子沿初速度方向做匀速直线运动,在偏转电场中的飞行时间设为t,则有
代入数据,可得
粒子飞出平行板时的侧移量
联立,可得
(4)粒子出场时的速度设为v,可以分解为沿初速度方向的v0和沿电场方向的vy,其中
根据勾股定理,可得
(5)根据恒力功的定义式,可得偏转场对粒子做的功为
代入数据,可得
17.(1),加速度方向垂直杆向下;(2)4J;(3)
【解析】(1)小环沿杆匀速下滑,受重力,电场力及支持力如图所示,由平衡条件可得
,
小环离开直杆后,只受重力及电场力作用,小环的加速度为
解得
, 加速度方向垂直杆向下
(2)小环从运动到过程中,由动能定理可得
解得
(3)小环从运动到过程中,做类平抛运动,如图所示有
代入数据联立解得
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
