2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2.1指数函数的概念教案(表格式)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2.1指数函数的概念教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 63.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 00:00:00 | ||
图片预览

文档简介
《指数函数的概念》教学设计
授课科目:数学 授课教师:
授课年级及班级:高一(8)班 授课时间:
学情分析: 授课对象为高一8班的学生,学生整体基础一般,但通过幂函数的学习,他们具备了一定的数学抽象和归纳总结的素养。在本节课之前,已经学过了幂函数,学习指数函数的概念过程可以类比于幂函数概念的形成过程。教材中指数函数的概念一节中,实际背景选取的问题1对于高一8班的同学而言会稍微有点难度,问题中出现的数据更会给学生的学习带来心理负担。因此,在教学过程中,我根据学情选取了“细胞分裂”的例子替换了教材中的问题1,在引入部分适当降低难度,帮助学生快速进入课题;再重点慢节奏的引导学生分析教材中的问题2,进而引导学生发现概括出指数函数的概念,体会概念形成的过程。概念形成后,先让学生观察其定义域的范围;再抛出问题,引导学生结合定义域分析对底数有何要求,最后通过习题来强化学生对指数函数概念的理解。
教学内容分析: 本节内容位于高中数学新人教版版教材必修一第四章第二节。指数函数是学生在学习了幂函数、有前一节指数内容做铺垫的基础上系统学习的一类新的基本初等函数。在函数部分的教学中起着承上启下的作用。学习指数函数的概念可类比与幂函数概念的形成过程,通过具体的实例,了解指数函数的实际意义并概括生成指数函数的概念。同时本节课的学习为后面研究指数函数的性质和学习对数函数打下了基础。因此,本节课的教学,重在引导学生结合实际背景来归纳指数函数的概念,培养数学抽象素养,提高数学建模的素养。
教学目标: 1.通过具体的实例,了解指数函数的实际意义,理解指数函数的概念与意义。 2.在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型。 3.通过学习指数函数的概念和意义,锻炼数学抽象素养;借助指数函数的实际应用,提升数学建模和数学运算素养。
教学重难点: 1.重点:指数函数的概念。 2.难点:指数函数概念的形成过程。
教学方法:讲授法
教学用具:PPT
教 学 过 程
教学环节及内容 设计意图 设计时间
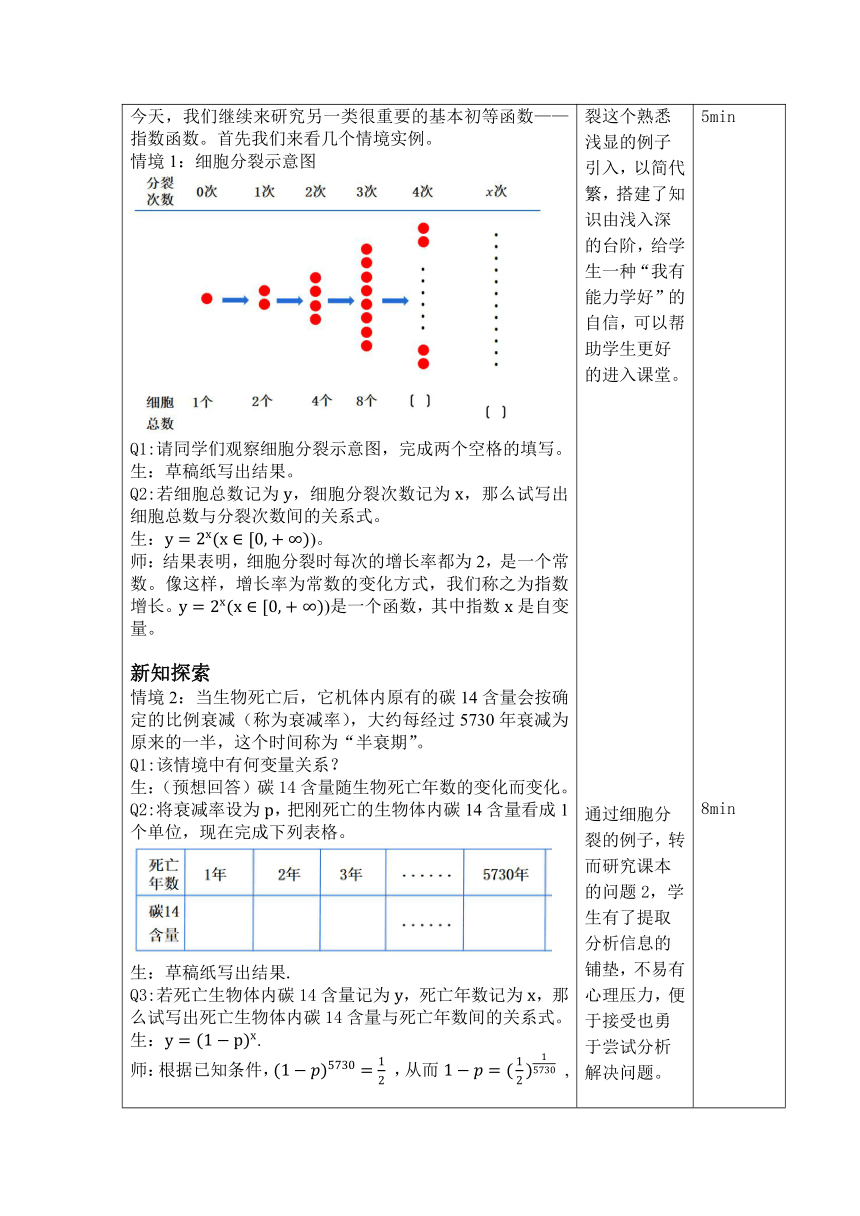
情境导入 师:上一章我们学习了函数的概念和基本性质,并通过对幂函数的研究,进一步了解了研究一类函数的过程和方法。今天,我们继续来研究另一类很重要的基本初等函数——指数函数。首先我们来看几个情境实例。 情境1:细胞分裂示意图 Q1:请同学们观察细胞分裂示意图,完成两个空格的填写。 生:草稿纸写出结果。 Q2:若细胞总数记为,细胞分裂次数记为,那么试写出细胞总数与分裂次数间的关系式。 生:)。 师:结果表明,细胞分裂时每次的增长率都为2,是一个常数。像这样,增长率为常数的变化方式,我们称之为指数增长。)是一个函数,其中指数是自变量。 新知探索 情境2:当生物死亡后,它机体内原有的碳14含量会按确定的比例衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”。 Q1:该情境中有何变量关系? 生:(预想回答)碳14含量随生物死亡年数的变化而变化。 Q2:将衰减率设为,把刚死亡的生物体内碳14含量看成1个单位,现在完成下列表格。 生:草稿纸写出结果. Q3:若死亡生物体内碳14含量记为,死亡年数记为,那么试写出死亡生物体内碳14含量与死亡年数间的关系式。 生:. 师:根据已知条件, ,从而 ,所以.那么就可以写为).这也是一个函数,指数是自变量。生物体内碳14的含量每年都以的衰减率衰减。像这样,衰减率为常数的变化方式,我们称之为指数衰减。 思考:请同学类比于幂函数概念,说出有什么特征?能否用一个式子反映这些特征? 生:底数是一个常数,指数是自变量,。 概念生成 师:中,对x有要求吗? 生:(预想回答)x可取一切实数。 师:那对有要求吗? 生:(预想回答)有,不能为负数…… 师:是的,但是不大全面。我们一起来看一下。 若,当时,无意义;若,当时,则无意义;若,是常数。 师:因此我们规定:且。 师:现在同学们能描述出指数函数的概念了吗? 生:(预想回答)一般地,函数(且)叫做指数函数。 师:(补充不足)其中指数x是自变量,定义域为R。 生:记录笔记。 师:和幂函数一样,在指数函数这里我们仍然有几个需要关注的点。 定义域必须是实数集R; 自变量是x,x位于指数位置上,且指数位置只能有x这一项; 底数a只能有一项,且其系数必须为1; 底数a的范围是且. 生:记录笔记。 练习巩固 例1.给出下列函数:①;②;③;④;⑤. 其中,指数函数的个数是( ). A.0 B.1 C.2 D.4 变1.若函数是指数函数,则a=_______ . 例2.已知指数函数(且),且 变2.甲、乙两城市现有人口总数都为100万人,甲城市人口的年增长率为1.2%,乙城市每年增长人口1.3万.试解决下面的问题: 写出两城市的人口总数(万人)与年份x(年)的函数解析式; 计算10年、20年、30年后两城市的人口总数(精确到0.1万人); 试对两城市人口增长情况做出分析。 小结&作业 师:本节课,我们主要学习了指数函数的概念。请同学们回顾一下,并说出需要注意的点。 生:(回答问题)…… 师:指数函数的概念至此已经结束了。请同学们预习好下一节的内容并完成以下作业: 复习本节课的笔记并预习好下一节内容; 课本P115练习1、 2、 3(只需要写出解析式即可)。 板书 主板:指数函数的概念及其注意的点。 副板:练习讲解过程书写。 教学反思 通过细胞分裂这个熟悉浅显的例子引入,以简代繁,搭建了知识由浅入深的台阶,给学生一种“我有能力学好”的自信,可以帮助学生更好的进入课堂。 通过细胞分裂的例子,转而研究课本的问题2,学生有了提取分析信息的铺垫,不易有心理压力,便于接受也勇于尝试分析解决问题。 不直接给出概念,学生先自己发现共性并尝试归纳。通过对定义域的讨论,来抛出问题:对底数a的要求,一方面充分发挥了学生的主观能动力,一方面可以巩固前一节根式的相关内容。 练为巩固,通过练习学生加强了对指数函数概念的理解;也体会到指数函数在生活中的应用。 5min 8min 7min 17min 3min
授课科目:数学 授课教师:
授课年级及班级:高一(8)班 授课时间:
学情分析: 授课对象为高一8班的学生,学生整体基础一般,但通过幂函数的学习,他们具备了一定的数学抽象和归纳总结的素养。在本节课之前,已经学过了幂函数,学习指数函数的概念过程可以类比于幂函数概念的形成过程。教材中指数函数的概念一节中,实际背景选取的问题1对于高一8班的同学而言会稍微有点难度,问题中出现的数据更会给学生的学习带来心理负担。因此,在教学过程中,我根据学情选取了“细胞分裂”的例子替换了教材中的问题1,在引入部分适当降低难度,帮助学生快速进入课题;再重点慢节奏的引导学生分析教材中的问题2,进而引导学生发现概括出指数函数的概念,体会概念形成的过程。概念形成后,先让学生观察其定义域的范围;再抛出问题,引导学生结合定义域分析对底数有何要求,最后通过习题来强化学生对指数函数概念的理解。
教学内容分析: 本节内容位于高中数学新人教版版教材必修一第四章第二节。指数函数是学生在学习了幂函数、有前一节指数内容做铺垫的基础上系统学习的一类新的基本初等函数。在函数部分的教学中起着承上启下的作用。学习指数函数的概念可类比与幂函数概念的形成过程,通过具体的实例,了解指数函数的实际意义并概括生成指数函数的概念。同时本节课的学习为后面研究指数函数的性质和学习对数函数打下了基础。因此,本节课的教学,重在引导学生结合实际背景来归纳指数函数的概念,培养数学抽象素养,提高数学建模的素养。
教学目标: 1.通过具体的实例,了解指数函数的实际意义,理解指数函数的概念与意义。 2.在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型。 3.通过学习指数函数的概念和意义,锻炼数学抽象素养;借助指数函数的实际应用,提升数学建模和数学运算素养。
教学重难点: 1.重点:指数函数的概念。 2.难点:指数函数概念的形成过程。
教学方法:讲授法
教学用具:PPT
教 学 过 程
教学环节及内容 设计意图 设计时间
情境导入 师:上一章我们学习了函数的概念和基本性质,并通过对幂函数的研究,进一步了解了研究一类函数的过程和方法。今天,我们继续来研究另一类很重要的基本初等函数——指数函数。首先我们来看几个情境实例。 情境1:细胞分裂示意图 Q1:请同学们观察细胞分裂示意图,完成两个空格的填写。 生:草稿纸写出结果。 Q2:若细胞总数记为,细胞分裂次数记为,那么试写出细胞总数与分裂次数间的关系式。 生:)。 师:结果表明,细胞分裂时每次的增长率都为2,是一个常数。像这样,增长率为常数的变化方式,我们称之为指数增长。)是一个函数,其中指数是自变量。 新知探索 情境2:当生物死亡后,它机体内原有的碳14含量会按确定的比例衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”。 Q1:该情境中有何变量关系? 生:(预想回答)碳14含量随生物死亡年数的变化而变化。 Q2:将衰减率设为,把刚死亡的生物体内碳14含量看成1个单位,现在完成下列表格。 生:草稿纸写出结果. Q3:若死亡生物体内碳14含量记为,死亡年数记为,那么试写出死亡生物体内碳14含量与死亡年数间的关系式。 生:. 师:根据已知条件, ,从而 ,所以.那么就可以写为).这也是一个函数,指数是自变量。生物体内碳14的含量每年都以的衰减率衰减。像这样,衰减率为常数的变化方式,我们称之为指数衰减。 思考:请同学类比于幂函数概念,说出有什么特征?能否用一个式子反映这些特征? 生:底数是一个常数,指数是自变量,。 概念生成 师:中,对x有要求吗? 生:(预想回答)x可取一切实数。 师:那对有要求吗? 生:(预想回答)有,不能为负数…… 师:是的,但是不大全面。我们一起来看一下。 若,当时,无意义;若,当时,则无意义;若,是常数。 师:因此我们规定:且。 师:现在同学们能描述出指数函数的概念了吗? 生:(预想回答)一般地,函数(且)叫做指数函数。 师:(补充不足)其中指数x是自变量,定义域为R。 生:记录笔记。 师:和幂函数一样,在指数函数这里我们仍然有几个需要关注的点。 定义域必须是实数集R; 自变量是x,x位于指数位置上,且指数位置只能有x这一项; 底数a只能有一项,且其系数必须为1; 底数a的范围是且. 生:记录笔记。 练习巩固 例1.给出下列函数:①;②;③;④;⑤. 其中,指数函数的个数是( ). A.0 B.1 C.2 D.4 变1.若函数是指数函数,则a=_______ . 例2.已知指数函数(且),且 变2.甲、乙两城市现有人口总数都为100万人,甲城市人口的年增长率为1.2%,乙城市每年增长人口1.3万.试解决下面的问题: 写出两城市的人口总数(万人)与年份x(年)的函数解析式; 计算10年、20年、30年后两城市的人口总数(精确到0.1万人); 试对两城市人口增长情况做出分析。 小结&作业 师:本节课,我们主要学习了指数函数的概念。请同学们回顾一下,并说出需要注意的点。 生:(回答问题)…… 师:指数函数的概念至此已经结束了。请同学们预习好下一节的内容并完成以下作业: 复习本节课的笔记并预习好下一节内容; 课本P115练习1、 2、 3(只需要写出解析式即可)。 板书 主板:指数函数的概念及其注意的点。 副板:练习讲解过程书写。 教学反思 通过细胞分裂这个熟悉浅显的例子引入,以简代繁,搭建了知识由浅入深的台阶,给学生一种“我有能力学好”的自信,可以帮助学生更好的进入课堂。 通过细胞分裂的例子,转而研究课本的问题2,学生有了提取分析信息的铺垫,不易有心理压力,便于接受也勇于尝试分析解决问题。 不直接给出概念,学生先自己发现共性并尝试归纳。通过对定义域的讨论,来抛出问题:对底数a的要求,一方面充分发挥了学生的主观能动力,一方面可以巩固前一节根式的相关内容。 练为巩固,通过练习学生加强了对指数函数概念的理解;也体会到指数函数在生活中的应用。 5min 8min 7min 17min 3min
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
