23.3 课题学习 图案设计 2021-2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 23.3 课题学习 图案设计 2021-2022学年人教版九年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 381.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 11:48:06 | ||
图片预览



文档简介
安徽省太和民族中学2021-2022学年上学期九年级数学基础练习
23.3课题学习 图案设计
一.选择题(本题共10道小题,每小题4分,满分40分)
1.下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A. B. C. D.
2.在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
A.2条 B.3条 C.4条 D.5条
3.静静制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )
4.如图所示的风车图案可以看做是由一个直角三角形通过五次旋转得到的,那么每次需要旋转的最小角度为( )
A.60° B.72° C.90° D.180°
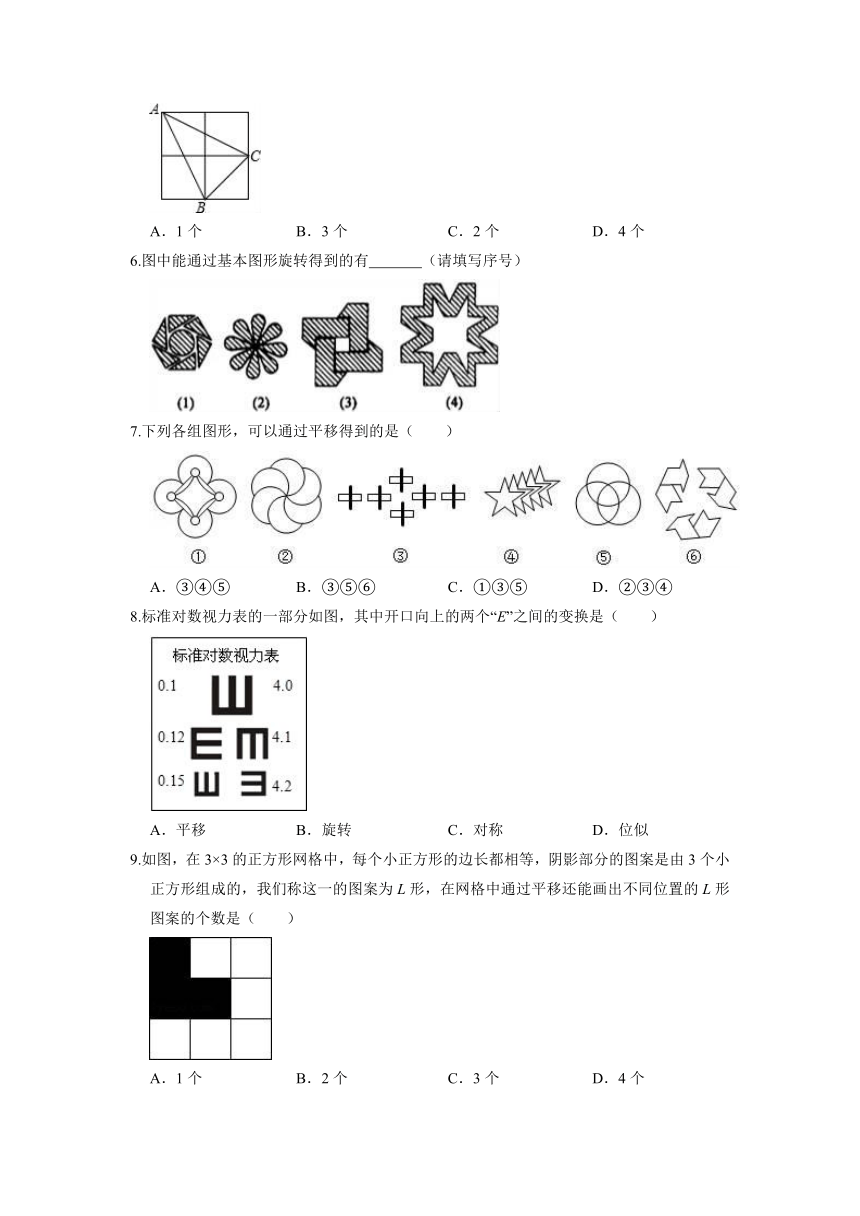
5.如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,则田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
6.图中能通过基本图形旋转得到的有 (请填写序号)
7.下列各组图形,可以通过平移得到的是( )
A.③④⑤ B.③⑤⑥ C.①③⑤ D.②③④
8.标准对数视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移 B.旋转 C.对称 D.位似
9.如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为L形,在网格中通过平移还能画出不同位置的L形图案的个数是( )
A.1个 B.2个 C.3个 D.4个
10.一个图形无论经过平移还是旋转,有以下说法:
(1)对应线段平行;
(2)对应线段相等;
(3)对应角相等;
(4)不改变图形的形状和大小,
其中正确的有( )
A.(3) B.(4) C.(4) D.(4)
二.填空题(本题共4道小题,每小题5分,满分20分)
11.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形,这样的白色小方格有 个,请在图中设计出一种方案.
12.如图所示,画出三角形ABC绕点C逆时针旋转90°后的图形 (画在图上)
13.仔细观察下列图案,并按规律在横线上画出合适的图形.
14.在五行五列的方格棋盘上沿骰子的某条棱翻动骰子,骰子在棋盘上只能向它所在格的左、右、前、后格翻动.开始时骰子在3C处,如图1,将骰子从3C处翻动一次到3B处,骰子的形态如图2;如果从3C处开始翻动两次,使朝上,骰子所在的位置是 .
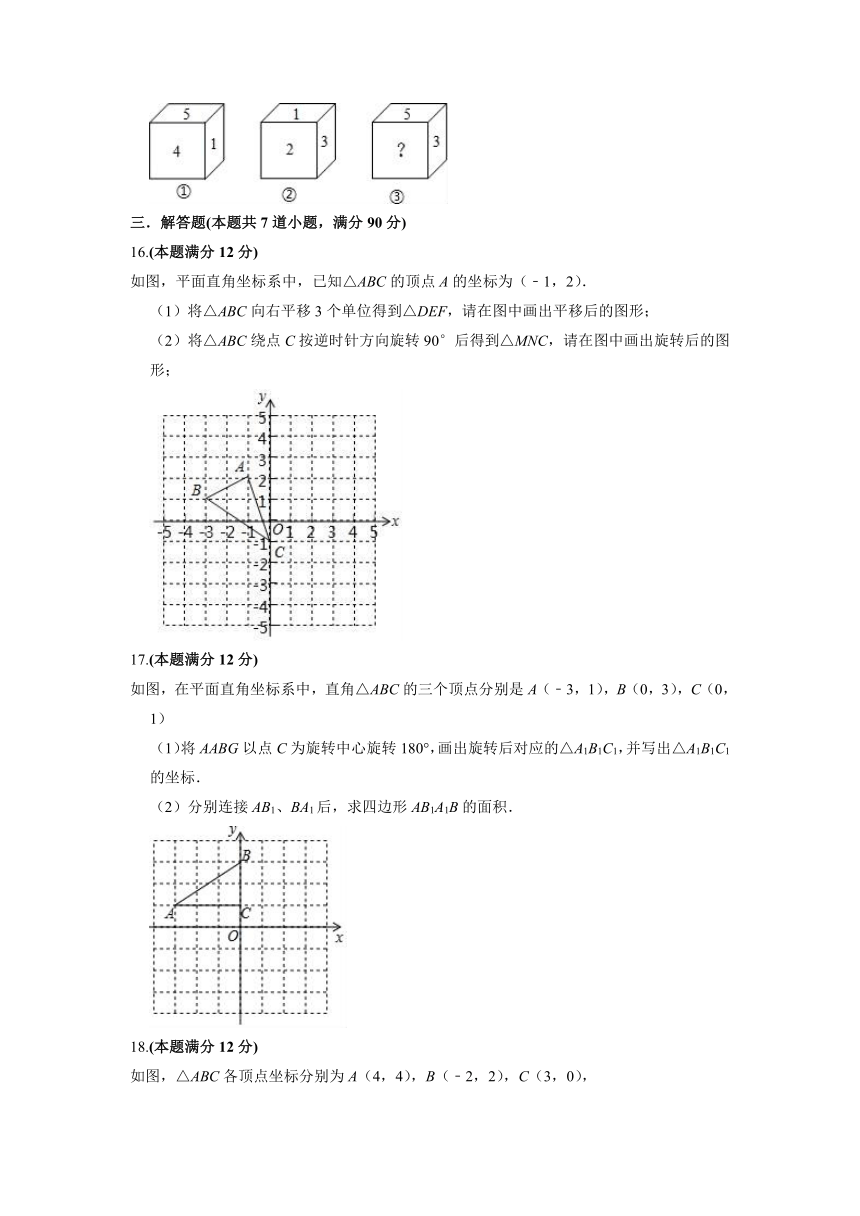
15.如图,一个正方体的每个面上分别标有数字1,2,3,4,5,6,根据图中该正方体①②③三种状态时所显示的数字,可推断“?”处的数字是 .
三.解答题(本题共7道小题,满分90分)
16.(本题满分12分)
如图,平面直角坐标系中,已知△ABC的顶点A的坐标为(﹣1,2).
(1)将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形;
(2)将△ABC绕点C按逆时针方向旋转90°后得到△MNC,请在图中画出旋转后的图形;
17.(本题满分12分)
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)
(1)将AABG以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,并写出△A1B1C1的坐标.
(2)分别连接AB1、BA1后,求四边形AB1A1B的面积.
18.(本题满分12分)
如图,△ABC各顶点坐标分别为A(4,4),B(﹣2,2),C(3,0),
①画出它的以原点O为对称中心的△A'B'C';
②在y轴上有一点P,使BP+C'P最小,求出P点坐标.
19.(本题满分12分)
如图,△ABC三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0)
(1)画出△ABC关于原点对称的三角形△A1B1C1;
(2)将三角形A、B、C绕坐标原点O逆时针旋转90°,得到△A2B2C2,请画出图形,并直写出点B的对应点B2的坐标;
(3)直接写出以A、B、C为顶点的平行四边形的第四个顶点的坐标.
20.(本题满分14分)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出将△ABC向下平移5个单位后的△A1B1C1.
(2)画出△ABC关于点B成中心对称的△A2BC2.
(3)画出△ABC绕点B逆时针旋转90°的△A3BC3.
(4)在直线上找一点P,使△ABP的周长最小(说明:在网格中画出图形,标上字母即可)
21.(本题满分14分)
如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请按要求画出图形,使得它们的顶点均在小正方形的顶点上
(1)在图中画一个以AB为边的菱形ABCD,使得菱形ABCD的面积为24;
(2)以B为旋转中心,将线段BA顺时针方向旋转90°得到线段BE.
(3)连接CE,则线段CE的长为 .
22.(本题满分14分)
如图,由4个全等的正方形组成L形图案,请你在图案中改变1个正方形的位置,使它变成轴对称图案.(只需画出3个)
参考答案
一.选择题
1.【解答】选:C.
2.【解答】解:如图所示:能满足条件的线段有4条.
故选:C.
3.【解答】选A
4.【解答】解:观察图象可知,每次需要旋转的最小角度==60°,
故选:A.
5.【解答】解:如图所示:符合题意的有3个三角形.
故选:B.
6.【解答】解:四幅图中,能通过基本图形旋转得到的有:(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
7.【解答】解:①要通过轴对称得到,故错误;
②通过旋转得到,故错误;
③图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
④图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
⑤图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
⑥要通过旋转和平移得到,故错误.
故选:A.
8.【解答】解:根据位似变换的特点可知它们之间的变换属于位似变换.故选D.
9.【解答】解:如图所示:1,2,3的位置可以组成图案为L.
故选:C.
10.【解答】解:一个图形无论经过平移还是旋转,对应线段和角相等,不改变图形的形状和大小,旋转后对应的线段可能不平行.
故选:D.
二.填空题(共5小题)
11.【解答】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
故选:C.
12.【解答】
【解答】解:应填E的对称图形,如图:
.
14.【解答】解:根据已知,可将骰子从3C处先翻滚一次到2C处,再翻滚一次到2B处,此时朝上;
或将骰子从3C处先翻滚一次到4C处,再翻滚一次到4B处,同样朝上.
故答案为:2B或4B.
15.【解答】解:∵1与2,3,4,5相邻,只能与6相对,2与5相对;3与4相对.当5在上,3在右时,前面只能是1.
故答案为:1.
解答题
16.解:(1)如图,△DEF为所作;
(2)如图,△MNC为所作.
16.【解答】解:(1)△A1B1C1如图所示,A1(3,1),B1(0,﹣1),C1(0,1).
(2)由题意四边形ABA1B1是菱形,∴.
17.【解答】解:①如图,△A'B'C'为所作;
②如图,BC于y轴的交点即为P点,
∵C点和C′点关于y轴对称,
∴PC=PC′,
∴BP+PC′=BP+PC=BC,
∴此时BP+C′P的值最小,
设直线BC的解析式为y=kx+b,
把B(﹣2,2),C(3,0)分别代入得,解得,
∴直线BC的解析式为,
∴P点坐标为.
18.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;点B2的坐标为(0,﹣6);
(3)以A、B、C为顶点的平行四边形的第四个顶点的坐标为(3,3)或(7,3)或(﹣5,﹣3).
19.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2BC2即为所求;
(3如图所示,△A3BC3即为所求;
(4)找出A关于直线l的对称点A′,连接A′B,交直线l于点P,P点即为所求.
解:(1)如图,四边形ABCD即为所求.
(2)如图,线段BE即为所求.
(3)EC=.
21.解:如图所示:
23.3课题学习 图案设计
一.选择题(本题共10道小题,每小题4分,满分40分)
1.下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A. B. C. D.
2.在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
A.2条 B.3条 C.4条 D.5条
3.静静制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )
4.如图所示的风车图案可以看做是由一个直角三角形通过五次旋转得到的,那么每次需要旋转的最小角度为( )
A.60° B.72° C.90° D.180°
5.如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,则田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
6.图中能通过基本图形旋转得到的有 (请填写序号)
7.下列各组图形,可以通过平移得到的是( )
A.③④⑤ B.③⑤⑥ C.①③⑤ D.②③④
8.标准对数视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移 B.旋转 C.对称 D.位似
9.如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为L形,在网格中通过平移还能画出不同位置的L形图案的个数是( )
A.1个 B.2个 C.3个 D.4个
10.一个图形无论经过平移还是旋转,有以下说法:
(1)对应线段平行;
(2)对应线段相等;
(3)对应角相等;
(4)不改变图形的形状和大小,
其中正确的有( )
A.(3) B.(4) C.(4) D.(4)
二.填空题(本题共4道小题,每小题5分,满分20分)
11.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形,这样的白色小方格有 个,请在图中设计出一种方案.
12.如图所示,画出三角形ABC绕点C逆时针旋转90°后的图形 (画在图上)
13.仔细观察下列图案,并按规律在横线上画出合适的图形.
14.在五行五列的方格棋盘上沿骰子的某条棱翻动骰子,骰子在棋盘上只能向它所在格的左、右、前、后格翻动.开始时骰子在3C处,如图1,将骰子从3C处翻动一次到3B处,骰子的形态如图2;如果从3C处开始翻动两次,使朝上,骰子所在的位置是 .
15.如图,一个正方体的每个面上分别标有数字1,2,3,4,5,6,根据图中该正方体①②③三种状态时所显示的数字,可推断“?”处的数字是 .
三.解答题(本题共7道小题,满分90分)
16.(本题满分12分)
如图,平面直角坐标系中,已知△ABC的顶点A的坐标为(﹣1,2).
(1)将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形;
(2)将△ABC绕点C按逆时针方向旋转90°后得到△MNC,请在图中画出旋转后的图形;
17.(本题满分12分)
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)
(1)将AABG以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,并写出△A1B1C1的坐标.
(2)分别连接AB1、BA1后,求四边形AB1A1B的面积.
18.(本题满分12分)
如图,△ABC各顶点坐标分别为A(4,4),B(﹣2,2),C(3,0),
①画出它的以原点O为对称中心的△A'B'C';
②在y轴上有一点P,使BP+C'P最小,求出P点坐标.
19.(本题满分12分)
如图,△ABC三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0)
(1)画出△ABC关于原点对称的三角形△A1B1C1;
(2)将三角形A、B、C绕坐标原点O逆时针旋转90°,得到△A2B2C2,请画出图形,并直写出点B的对应点B2的坐标;
(3)直接写出以A、B、C为顶点的平行四边形的第四个顶点的坐标.
20.(本题满分14分)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出将△ABC向下平移5个单位后的△A1B1C1.
(2)画出△ABC关于点B成中心对称的△A2BC2.
(3)画出△ABC绕点B逆时针旋转90°的△A3BC3.
(4)在直线上找一点P,使△ABP的周长最小(说明:在网格中画出图形,标上字母即可)
21.(本题满分14分)
如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请按要求画出图形,使得它们的顶点均在小正方形的顶点上
(1)在图中画一个以AB为边的菱形ABCD,使得菱形ABCD的面积为24;
(2)以B为旋转中心,将线段BA顺时针方向旋转90°得到线段BE.
(3)连接CE,则线段CE的长为 .
22.(本题满分14分)
如图,由4个全等的正方形组成L形图案,请你在图案中改变1个正方形的位置,使它变成轴对称图案.(只需画出3个)
参考答案
一.选择题
1.【解答】选:C.
2.【解答】解:如图所示:能满足条件的线段有4条.
故选:C.
3.【解答】选A
4.【解答】解:观察图象可知,每次需要旋转的最小角度==60°,
故选:A.
5.【解答】解:如图所示:符合题意的有3个三角形.
故选:B.
6.【解答】解:四幅图中,能通过基本图形旋转得到的有:(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
7.【解答】解:①要通过轴对称得到,故错误;
②通过旋转得到,故错误;
③图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
④图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
⑤图形的形状和大小没有改变,只是位置发生了变化,符合平移性质,故正确;
⑥要通过旋转和平移得到,故错误.
故选:A.
8.【解答】解:根据位似变换的特点可知它们之间的变换属于位似变换.故选D.
9.【解答】解:如图所示:1,2,3的位置可以组成图案为L.
故选:C.
10.【解答】解:一个图形无论经过平移还是旋转,对应线段和角相等,不改变图形的形状和大小,旋转后对应的线段可能不平行.
故选:D.
二.填空题(共5小题)
11.【解答】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
故选:C.
12.【解答】
【解答】解:应填E的对称图形,如图:
.
14.【解答】解:根据已知,可将骰子从3C处先翻滚一次到2C处,再翻滚一次到2B处,此时朝上;
或将骰子从3C处先翻滚一次到4C处,再翻滚一次到4B处,同样朝上.
故答案为:2B或4B.
15.【解答】解:∵1与2,3,4,5相邻,只能与6相对,2与5相对;3与4相对.当5在上,3在右时,前面只能是1.
故答案为:1.
解答题
16.解:(1)如图,△DEF为所作;
(2)如图,△MNC为所作.
16.【解答】解:(1)△A1B1C1如图所示,A1(3,1),B1(0,﹣1),C1(0,1).
(2)由题意四边形ABA1B1是菱形,∴.
17.【解答】解:①如图,△A'B'C'为所作;
②如图,BC于y轴的交点即为P点,
∵C点和C′点关于y轴对称,
∴PC=PC′,
∴BP+PC′=BP+PC=BC,
∴此时BP+C′P的值最小,
设直线BC的解析式为y=kx+b,
把B(﹣2,2),C(3,0)分别代入得,解得,
∴直线BC的解析式为,
∴P点坐标为.
18.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;点B2的坐标为(0,﹣6);
(3)以A、B、C为顶点的平行四边形的第四个顶点的坐标为(3,3)或(7,3)或(﹣5,﹣3).
19.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2BC2即为所求;
(3如图所示,△A3BC3即为所求;
(4)找出A关于直线l的对称点A′,连接A′B,交直线l于点P,P点即为所求.
解:(1)如图,四边形ABCD即为所求.
(2)如图,线段BE即为所求.
(3)EC=.
21.解:如图所示:
同课章节目录
