第4章图形的相似 单元达标测评 2021-2022学年北师大版九年级数学上册(word版含答案)
文档属性
| 名称 | 第4章图形的相似 单元达标测评 2021-2022学年北师大版九年级数学上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《第4章图形的相似》单元达标测评(附答案)
一.选择题(共10小题,满分50分)
1.如果x:y=3:5,那么x:(x+y)=( )
A. B. C. D.
2.若△ABC≌△DEF,若∠A=50°,则∠D的度数是( )
A.50° B.60° C.70° D.80°
3.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
4.有一个多边形的各边长分别为4cm,5cm,6cm,4cm,5cm,和它相似的另一个多边形的最长边为9cm,则这个多边形的周长是( )
A.12cm B.18cm C.36cm D.48cm
5.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
6.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
7.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
8.如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( )
A.3.5 B.4 C.4.5 D.5
9.如图,已知线段AB,过点B作AB的垂线,并在垂线上取BC=AB;连接AC,以点C为圆心,CB为半径画弧,交AC于点D;再以点A为圆心,AD为半径画弧,交AB于点P,则的值是( )
A. B. C. D.
10.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
二.填空题(共6小题,满分30分)
11.已知:AB=2m,CD=28cm,则AB:CD= .
12.如图,若点C是AB的黄金分割点(AC>BC),AB=8,则BC的长为 .
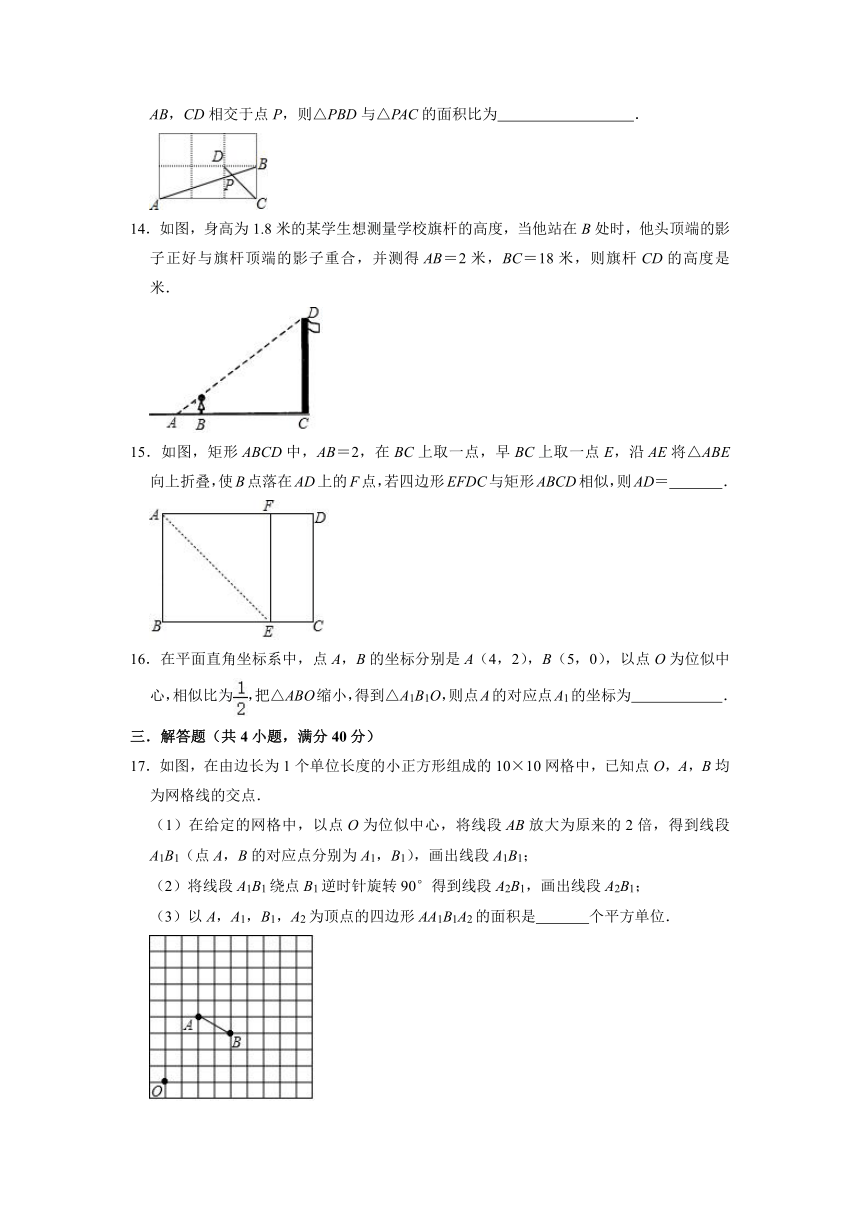
13.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则△PBD与△PAC的面积比为 .
14.如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是 米.
15.如图,矩形ABCD中,AB=2,在BC上取一点,早BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
16.在平面直角坐标系中,点A,B的坐标分别是A(4,2),B(5,0),以点O为位似中心,相似比为,把△ABO缩小,得到△A1B1O,则点A的对应点A1的坐标为 .
三.解答题(共4小题,满分40分)
17.如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),画出线段A1B1;
(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,画出线段A2B1;
(3)以A,A1,B1,A2为顶点的四边形AA1B1A2的面积是 个平方单位.
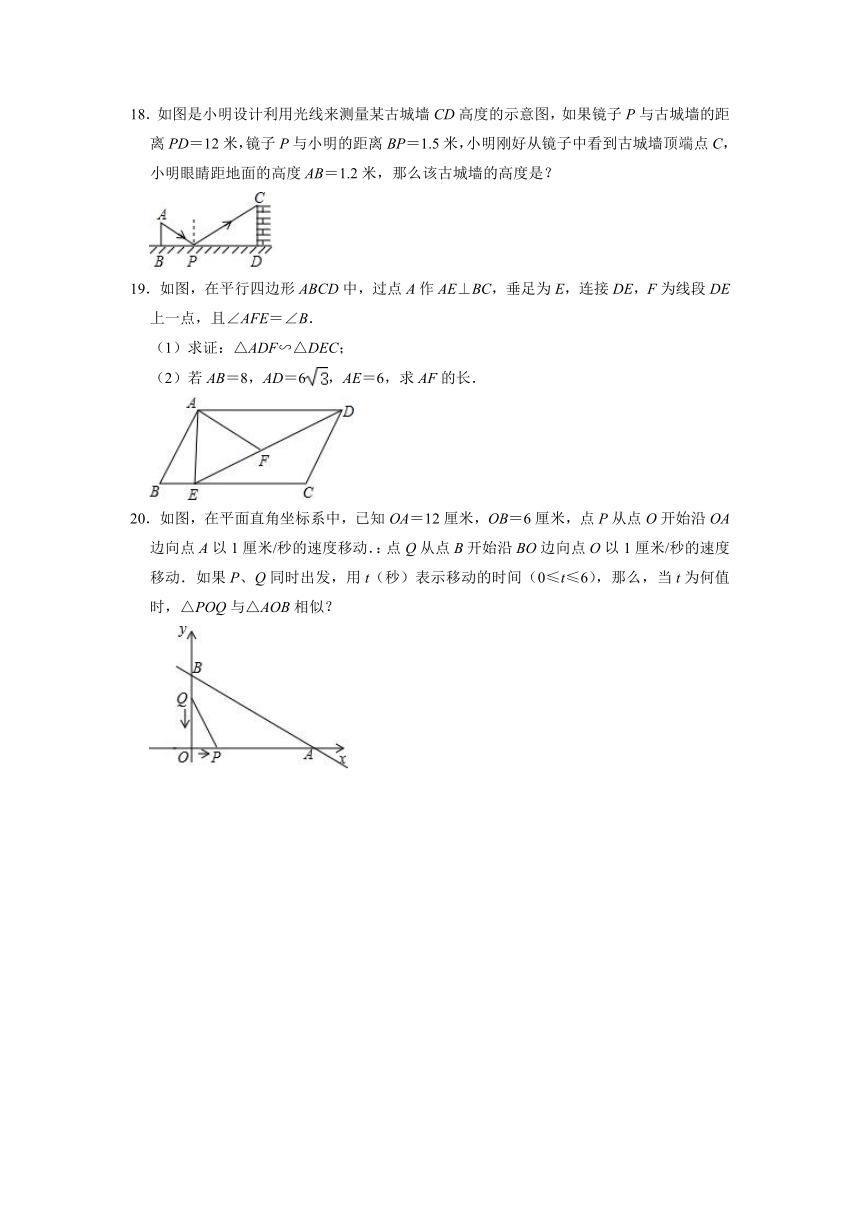
18.如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是?
19.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AE=6,求AF的长.
20.如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米,点P从点O开始沿OA边向点A以1厘米/秒的速度移动.:点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
参考答案
一.选择题(共10小题,满分50分)
1.解:∵x:y=3:5,
∴可设x=3k,则y=5k,
则x:(x+y)=3k:(3k+5k)=3:8;
故选:B.
2.解:∵△ABC≌△DEF,∠A=50°,
∴∠D=∠A=50°.
故选:A.
3.解:∵AB∥CD∥EF,
∴,
∴BE===10,
∴CE=BE﹣BC=10﹣6=4,
故选:B.
4.解:各边长分别为4cm,5cm,6cm,4cm,5cm,的多边形的周长是24cm.
和它相似的另一个多边形的最长边为9cm,
则这两个多边形的相似比是6:9=2:3,
设这个多边形的周长是xcm.
则x:24=2:3
解得:x=36cm.
这个多边形的周长是36cm.
故选:C.
5.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
6.解:依题意有△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD﹣AB=62.5﹣5=57.5尺.
故选:B.
7.解:①相似图形不一定是位似图形,位似图形一定是相似图形,故①错误;
②位似图形一定有位似中心,故②正确;
③如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.故③正确;
④位似图形上任意一对对应点到位似中心的距离之比等于位似比,故④错误.
正确的选项为:②.
故选:A.
8.解:∵AB=AC,
∴∠B=∠C;
又∵∠FDE=∠B,
∴∠BFD+∠BDF=∠BDF+∠CDE,
∴∠BFD=∠CDE,而∠B=∠C,
∴△BDF∽△CED,
∴BD:CE=BF:DC,
而BD=2,CD=3,CE=4,
∴BF=1.5,
∵AB=AC=1+4=5,
∴AF=5﹣1.5=3.5.
故选:A.
9.解:∵BC⊥AB,
∴∠ABC=90°,
设AB=2a,BC=a,则AC=a,
∵CD=BC=a,
∴AD=AC﹣CD=(﹣1)a,
∵AP=AD,
∴AP=(﹣1)a,
∴=.
故选:A.
10.解:∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴=,=,
∴+=+==1.
∵AB=1,CD=3,
∴+=1,
∴EF=.
故选:C.
二.填空题(共6小题,满分30分)
11.解:∵AB=2m=200cm,CD=28cm,
∴AB:CD=200:28=50:7.
故答案为50:7.
12.解:由题意知:BC=,
故答案为:12﹣4
13.解:∵BD∥AC,BD=1,AC=3,
∴△DBP∽△CAP,
∴=()2=,
故答案为.
14.解:如图:
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴△ABE∽△ACD,
∴=,
∴=,
解得:CD=18.
故答案为:18.
15.解:∵AB=2,
设AD=x,则FD=x﹣2,FE=2,
∵四边形EFDC与矩形ABCD相似,
∴=,=,
解得x1=1+,x2=1﹣(不合题意舍去),
经检验x1=1+是原方程的解.
故答案为:1+.
16.解:以点O为位似中心,相似比为,把△ABO缩小,点A的坐标是A(4,2),
则点A的对应点A1的坐标为(4×,2×)或(﹣4×,﹣2×),即(2,1)或(﹣2,﹣1),
故答案为:(2,1)或(﹣2,﹣1).
三.解答题(共4小题,满分40分)
17.解:(1)如图所示,线段A1B1即为所求;
(2)如图所示,线段A2B1即为所求;
(3)由图可得,四边形AA1B1A2为正方形,
∴四边形AA1B1A2的面积是()2=()2=20.
故答案为:20.
18.解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=,
即:=,
解得:PD=9.6(米).
答:该古城墙的高度是9.6m.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵CD=AB=8,AE⊥BC,
∴AE⊥AD;
在Rt△ADE中,DE==12,
∵△ADF∽△DEC,
∴;
∴
∴AF=4.
20.解:①若△POQ∽△AOB时,=,即=,
整理得:12﹣2t=t,
解得:t=4.
②若△POQ∽△BOA时,=,即=,
整理得:6﹣t=2t,
解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
一.选择题(共10小题,满分50分)
1.如果x:y=3:5,那么x:(x+y)=( )
A. B. C. D.
2.若△ABC≌△DEF,若∠A=50°,则∠D的度数是( )
A.50° B.60° C.70° D.80°
3.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
4.有一个多边形的各边长分别为4cm,5cm,6cm,4cm,5cm,和它相似的另一个多边形的最长边为9cm,则这个多边形的周长是( )
A.12cm B.18cm C.36cm D.48cm
5.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
6.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
7.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
8.如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( )
A.3.5 B.4 C.4.5 D.5
9.如图,已知线段AB,过点B作AB的垂线,并在垂线上取BC=AB;连接AC,以点C为圆心,CB为半径画弧,交AC于点D;再以点A为圆心,AD为半径画弧,交AB于点P,则的值是( )
A. B. C. D.
10.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
二.填空题(共6小题,满分30分)
11.已知:AB=2m,CD=28cm,则AB:CD= .
12.如图,若点C是AB的黄金分割点(AC>BC),AB=8,则BC的长为 .
13.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则△PBD与△PAC的面积比为 .
14.如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是 米.
15.如图,矩形ABCD中,AB=2,在BC上取一点,早BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
16.在平面直角坐标系中,点A,B的坐标分别是A(4,2),B(5,0),以点O为位似中心,相似比为,把△ABO缩小,得到△A1B1O,则点A的对应点A1的坐标为 .
三.解答题(共4小题,满分40分)
17.如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),画出线段A1B1;
(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,画出线段A2B1;
(3)以A,A1,B1,A2为顶点的四边形AA1B1A2的面积是 个平方单位.
18.如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是?
19.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AE=6,求AF的长.
20.如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米,点P从点O开始沿OA边向点A以1厘米/秒的速度移动.:点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
参考答案
一.选择题(共10小题,满分50分)
1.解:∵x:y=3:5,
∴可设x=3k,则y=5k,
则x:(x+y)=3k:(3k+5k)=3:8;
故选:B.
2.解:∵△ABC≌△DEF,∠A=50°,
∴∠D=∠A=50°.
故选:A.
3.解:∵AB∥CD∥EF,
∴,
∴BE===10,
∴CE=BE﹣BC=10﹣6=4,
故选:B.
4.解:各边长分别为4cm,5cm,6cm,4cm,5cm,的多边形的周长是24cm.
和它相似的另一个多边形的最长边为9cm,
则这两个多边形的相似比是6:9=2:3,
设这个多边形的周长是xcm.
则x:24=2:3
解得:x=36cm.
这个多边形的周长是36cm.
故选:C.
5.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
6.解:依题意有△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD﹣AB=62.5﹣5=57.5尺.
故选:B.
7.解:①相似图形不一定是位似图形,位似图形一定是相似图形,故①错误;
②位似图形一定有位似中心,故②正确;
③如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.故③正确;
④位似图形上任意一对对应点到位似中心的距离之比等于位似比,故④错误.
正确的选项为:②.
故选:A.
8.解:∵AB=AC,
∴∠B=∠C;
又∵∠FDE=∠B,
∴∠BFD+∠BDF=∠BDF+∠CDE,
∴∠BFD=∠CDE,而∠B=∠C,
∴△BDF∽△CED,
∴BD:CE=BF:DC,
而BD=2,CD=3,CE=4,
∴BF=1.5,
∵AB=AC=1+4=5,
∴AF=5﹣1.5=3.5.
故选:A.
9.解:∵BC⊥AB,
∴∠ABC=90°,
设AB=2a,BC=a,则AC=a,
∵CD=BC=a,
∴AD=AC﹣CD=(﹣1)a,
∵AP=AD,
∴AP=(﹣1)a,
∴=.
故选:A.
10.解:∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴=,=,
∴+=+==1.
∵AB=1,CD=3,
∴+=1,
∴EF=.
故选:C.
二.填空题(共6小题,满分30分)
11.解:∵AB=2m=200cm,CD=28cm,
∴AB:CD=200:28=50:7.
故答案为50:7.
12.解:由题意知:BC=,
故答案为:12﹣4
13.解:∵BD∥AC,BD=1,AC=3,
∴△DBP∽△CAP,
∴=()2=,
故答案为.
14.解:如图:
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴△ABE∽△ACD,
∴=,
∴=,
解得:CD=18.
故答案为:18.
15.解:∵AB=2,
设AD=x,则FD=x﹣2,FE=2,
∵四边形EFDC与矩形ABCD相似,
∴=,=,
解得x1=1+,x2=1﹣(不合题意舍去),
经检验x1=1+是原方程的解.
故答案为:1+.
16.解:以点O为位似中心,相似比为,把△ABO缩小,点A的坐标是A(4,2),
则点A的对应点A1的坐标为(4×,2×)或(﹣4×,﹣2×),即(2,1)或(﹣2,﹣1),
故答案为:(2,1)或(﹣2,﹣1).
三.解答题(共4小题,满分40分)
17.解:(1)如图所示,线段A1B1即为所求;
(2)如图所示,线段A2B1即为所求;
(3)由图可得,四边形AA1B1A2为正方形,
∴四边形AA1B1A2的面积是()2=()2=20.
故答案为:20.
18.解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=,
即:=,
解得:PD=9.6(米).
答:该古城墙的高度是9.6m.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵CD=AB=8,AE⊥BC,
∴AE⊥AD;
在Rt△ADE中,DE==12,
∵△ADF∽△DEC,
∴;
∴
∴AF=4.
20.解:①若△POQ∽△AOB时,=,即=,
整理得:12﹣2t=t,
解得:t=4.
②若△POQ∽△BOA时,=,即=,
整理得:6﹣t=2t,
解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
