人教版八年级下册数学 第十八章达标检测卷(word版含答案)
文档属性
| 名称 | 人教版八年级下册数学 第十八章达标检测卷(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 520.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 00:00:00 | ||
图片预览




文档简介
第十八章达标检测卷
一、选择题(每题3分,共30分)
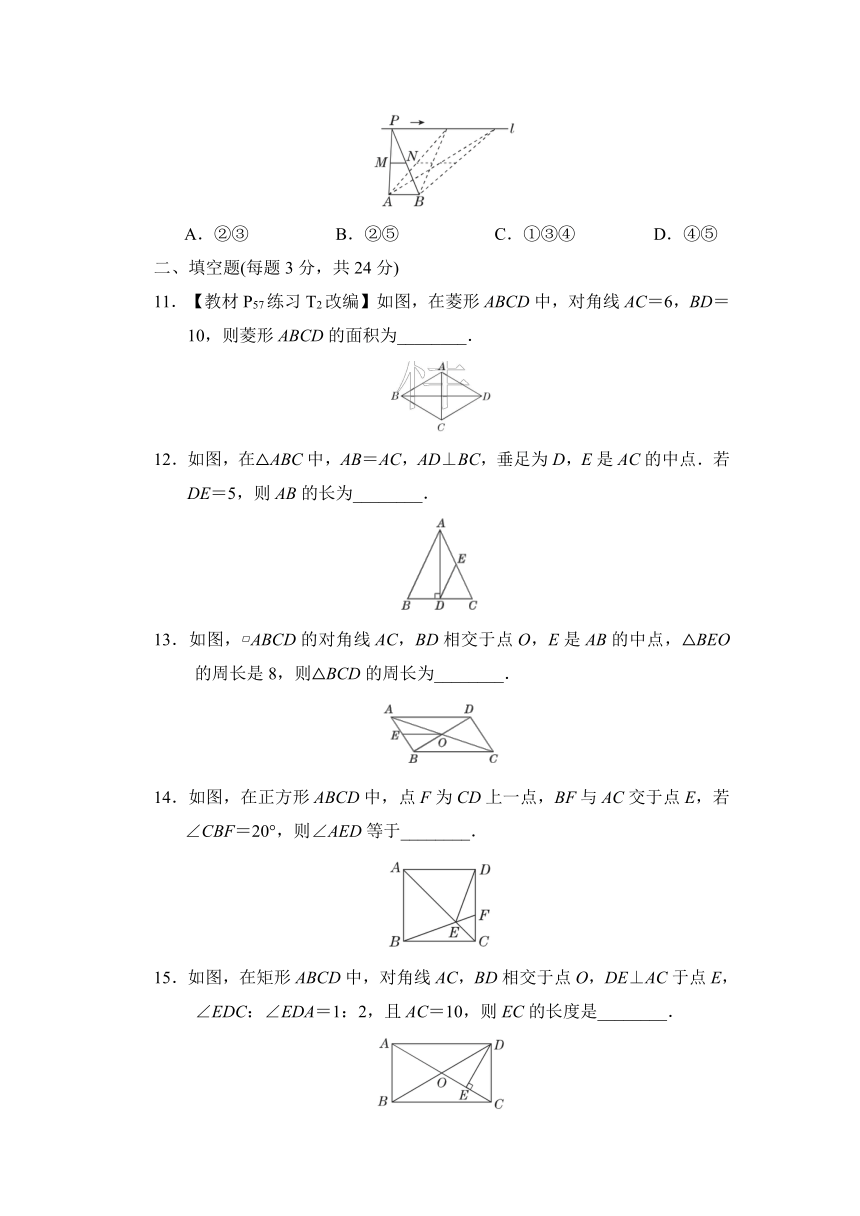
1.如图,D,E分别是△ABC的边AB,AC的中点,若DE=4,则BC的长为( )
A.2 B.4 C.6 D.8
2.如图,在 ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则BC的长是( )
A.6 cm B.6.5 cm C.7 cm D.7.5 cm
3.如图,四边形 ABCD 的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
4.下列结论,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
5.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列不能作为平行四边形顶点坐标的是( )
A.(3, 1) B.(-4,1) C.(1,-1) D.(-3,1)
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12 B.18 C.24 D.30
8.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.67.5° B.22.5° C.30° D.45°
9.【教材P50习题T8变式】如图,在平面直角坐标中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为( )
A.(2,) B.(,2) C.(,3) D.(3,)
10.【教材P50习题T7拓展】如图,点A,B为定点,定直线l∥AB,P是l上一动点,M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
二、填空题(每题3分,共24分)
11.【教材P57练习T2改编】如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
12.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=5,则AB的长为________.
13.如图, ABCD的对角线AC,BD相交于点O,E是AB的中点,△BEO的周长是8,则△BCD的周长为________.
14.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED等于________.
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=10,则EC的长度是________.
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF=________.
17.如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,它的周长为____________.
18.将两条邻边长分别为,1的长方形纸片剪成四张等腰三角形纸片(无剩余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的____________(填序号).
①;②1;③-1;④;⑤.
三、解答题(19题8分,20题10分,其余每题12分,共66分)
19.如图,在 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于点E,F.求证AE=CF.
20.如图,在 ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=________°时,四边形BECD是矩形.
21.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接CD,过点E作EF∥DC交BC的延长线于点F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25 cm,AC的长为5 cm,求线段AB的长度.
22.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4, BC=8,求菱形AECF的周长.
23.如图,在正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,
AF=AE.
(1)BF与DE有怎样的数量关系?请证明你的结论.
(2)在其他条件都保持不变的情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
24.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的
关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之
间的关系.
答案
一、1.D 2.C 3.C 4.C 5.C 6.B
7.C 点拨:根据题意易知△COF的面积与△AOE的面积相等,阴影部分的面积为矩形面积的四分之一.
8.B
9.D 点拨:如图,过点E作EF⊥x轴于点F.
∵四边形OABC为菱形,∠AOC=60°,
∴AC⊥OB,∠AOE=∠AOC=30°.∴∠FAE=60°.
∴∠FEA=30°.
∵A(4,0),∴OA=4.
∴AE=AO=×4=2.∴AF=AE=1.
∴EF===.OF=AO-AF=4-1=3.
∴E(3,).
10.B 点拨:∵点A,B为定点,M,N分别为PA,PB的中点,
∴MN是△PAB的中位线.
∴MN=AB,即线段MN的长度不变.
∵PA,PB的长度随点P的移动而变化,
∴△PAB的周长会随点P的移动而变化.
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变;
直线MN,AB之间的距离不随点P的移动而变化;
∠APB的大小随点P的移动而变化.
综上所述,会随点P的移动而变化的是②⑤.
二、11.30 12.10 13.16 14.65° 15.2.5 16.
17.16或20 点拨:如图所示.
①当AE=2,DE=4时,∵四边形ABCD是平行四边形,
∴BC=AD=6,AB=CD,AD∥BC.
∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠ABE=∠AEB.
∴AB=AE=2.
∴平行四边形ABCD的周长为2(AB+AD)=16.
②当AE=4,DE=2时,同理可得AB=AE=4,
平行四边形ABCD的周长为2(AB+AD)=20.
综上所述,所求的周长为16或20.
18.①②③④ 点拨:如图:
则其中一个等腰三角形的腰长可以是,1,-1,,不可以是 .
三、19.证明:∵四边形ABCD为平行四边形,
∴AD=BC,∠D=∠B,∠BAD=∠BCD.
又∵AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BAD,∠BCF=∠BCD.
∴∠DAE=∠BCF.
在△DAE和△BCF中,
∴△DAE≌△BCF(ASA).
∴AE=CF.
20.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC.
∴∠OEB=∠ODC.
∵O为BC的中点,∴BO=CO.
在△BOE和△COD中,
∴△BOE≌△COD(AAS).
∴OE=OD.
又∵BO=CO,∴四边形BECD是平行四边形.
(2)100
21.解:(1)证明:∵D,E分别是AB,AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线.
∴ED∥FC.
又∵EF∥DC,∴四边形CDEF是平行四边形.
(2)∵四边形CDEF是平行四边形,∴DC=EF.
∵DC是Rt△ABC斜边AB上的中线,∴AB=2DC.
又∵ED是Rt△ABC的中位线,
∴BC=2DE.
∴四边形CDEF的周长为AB+BC.
∵在Rt△ABC中,∠ACB=90°,∴AB2=BC2+AC2,
即AB2=(25-AB)2+52,解得AB=13 cm.
∴线段AB的长度为13 cm.
22.(1)证明:∵EF是AC的垂直平分线,
∴AO=OC,∠AOE=∠COF=90°.
∵四边形ABCD是矩形,∴AD∥BC.
∴∠EAO=∠FCO.
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA).
∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
又∵EF⊥AC,∴四边形AECF是菱形.
(2)解:设AF=x.
∵EF是AC的垂直平分线,∴AF=CF=x.
∴BF=8-x.
在Rt△ABF中,由勾股定理得: AB2+BF2=AF2,
即42+(8-x)2=x2,解得x=5.
∴AF=5.
∴菱形AECF的周长为4×5=20.
23.解:(1)BF=DE.证明如下:
∵四边形ABCD是正方形,
∴AB=AD,∠DAC=∠BAC=45°.
∵AF⊥AC,∴∠BAF=∠BAC=∠DAC=45°.
又∵AB=AD,AF=AE.
∴△AFB≌△AED(SAS).
∴BF=DE.
(2)四边形AFBE是正方形.证明如下:
∵四边形ABCD是正方形,E是AC的中点,∴AE=BE.
在△ABF和△ABE中,
∴△ABF≌△ABE(SAS).
∴BF=BE.
∴AE=BE=BF=AF.
∴四边形AFBE是菱形.
又∵AF⊥AE,∴四边形AFBE是正方形.
24.解:(1)AB=CG-CE.证明如下:
∵四边形ABCD是菱形,∴AB=BC.
又∵∠BAC=60°,∴△ABC是等边三角形.
∴AB=AC.
∵∠EAG=60°,∴∠BAC=∠EAG.
∴∠BAC+∠CAE=∠EAG+∠CAE,
即∠BAE=∠CAG.
又∵四边形AEFG是菱形,
∴AE=AG.
在△ABE和△ACG中,
∴△ABE≌△ACG(SAS).
∴BE=CG.
∵AB=BC=BE-CE,
∴AB=CG-CE.
(2)AB=CE-CG.
一、选择题(每题3分,共30分)
1.如图,D,E分别是△ABC的边AB,AC的中点,若DE=4,则BC的长为( )
A.2 B.4 C.6 D.8
2.如图,在 ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则BC的长是( )
A.6 cm B.6.5 cm C.7 cm D.7.5 cm
3.如图,四边形 ABCD 的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
4.下列结论,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
5.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列不能作为平行四边形顶点坐标的是( )
A.(3, 1) B.(-4,1) C.(1,-1) D.(-3,1)
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12 B.18 C.24 D.30
8.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.67.5° B.22.5° C.30° D.45°
9.【教材P50习题T8变式】如图,在平面直角坐标中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为( )
A.(2,) B.(,2) C.(,3) D.(3,)
10.【教材P50习题T7拓展】如图,点A,B为定点,定直线l∥AB,P是l上一动点,M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
二、填空题(每题3分,共24分)
11.【教材P57练习T2改编】如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
12.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=5,则AB的长为________.
13.如图, ABCD的对角线AC,BD相交于点O,E是AB的中点,△BEO的周长是8,则△BCD的周长为________.
14.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED等于________.
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=10,则EC的长度是________.
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF=________.
17.如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,它的周长为____________.
18.将两条邻边长分别为,1的长方形纸片剪成四张等腰三角形纸片(无剩余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的____________(填序号).
①;②1;③-1;④;⑤.
三、解答题(19题8分,20题10分,其余每题12分,共66分)
19.如图,在 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于点E,F.求证AE=CF.
20.如图,在 ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=________°时,四边形BECD是矩形.
21.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接CD,过点E作EF∥DC交BC的延长线于点F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25 cm,AC的长为5 cm,求线段AB的长度.
22.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4, BC=8,求菱形AECF的周长.
23.如图,在正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,
AF=AE.
(1)BF与DE有怎样的数量关系?请证明你的结论.
(2)在其他条件都保持不变的情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
24.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的
关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之
间的关系.
答案
一、1.D 2.C 3.C 4.C 5.C 6.B
7.C 点拨:根据题意易知△COF的面积与△AOE的面积相等,阴影部分的面积为矩形面积的四分之一.
8.B
9.D 点拨:如图,过点E作EF⊥x轴于点F.
∵四边形OABC为菱形,∠AOC=60°,
∴AC⊥OB,∠AOE=∠AOC=30°.∴∠FAE=60°.
∴∠FEA=30°.
∵A(4,0),∴OA=4.
∴AE=AO=×4=2.∴AF=AE=1.
∴EF===.OF=AO-AF=4-1=3.
∴E(3,).
10.B 点拨:∵点A,B为定点,M,N分别为PA,PB的中点,
∴MN是△PAB的中位线.
∴MN=AB,即线段MN的长度不变.
∵PA,PB的长度随点P的移动而变化,
∴△PAB的周长会随点P的移动而变化.
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变;
直线MN,AB之间的距离不随点P的移动而变化;
∠APB的大小随点P的移动而变化.
综上所述,会随点P的移动而变化的是②⑤.
二、11.30 12.10 13.16 14.65° 15.2.5 16.
17.16或20 点拨:如图所示.
①当AE=2,DE=4时,∵四边形ABCD是平行四边形,
∴BC=AD=6,AB=CD,AD∥BC.
∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠ABE=∠AEB.
∴AB=AE=2.
∴平行四边形ABCD的周长为2(AB+AD)=16.
②当AE=4,DE=2时,同理可得AB=AE=4,
平行四边形ABCD的周长为2(AB+AD)=20.
综上所述,所求的周长为16或20.
18.①②③④ 点拨:如图:
则其中一个等腰三角形的腰长可以是,1,-1,,不可以是 .
三、19.证明:∵四边形ABCD为平行四边形,
∴AD=BC,∠D=∠B,∠BAD=∠BCD.
又∵AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BAD,∠BCF=∠BCD.
∴∠DAE=∠BCF.
在△DAE和△BCF中,
∴△DAE≌△BCF(ASA).
∴AE=CF.
20.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC.
∴∠OEB=∠ODC.
∵O为BC的中点,∴BO=CO.
在△BOE和△COD中,
∴△BOE≌△COD(AAS).
∴OE=OD.
又∵BO=CO,∴四边形BECD是平行四边形.
(2)100
21.解:(1)证明:∵D,E分别是AB,AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线.
∴ED∥FC.
又∵EF∥DC,∴四边形CDEF是平行四边形.
(2)∵四边形CDEF是平行四边形,∴DC=EF.
∵DC是Rt△ABC斜边AB上的中线,∴AB=2DC.
又∵ED是Rt△ABC的中位线,
∴BC=2DE.
∴四边形CDEF的周长为AB+BC.
∵在Rt△ABC中,∠ACB=90°,∴AB2=BC2+AC2,
即AB2=(25-AB)2+52,解得AB=13 cm.
∴线段AB的长度为13 cm.
22.(1)证明:∵EF是AC的垂直平分线,
∴AO=OC,∠AOE=∠COF=90°.
∵四边形ABCD是矩形,∴AD∥BC.
∴∠EAO=∠FCO.
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA).
∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
又∵EF⊥AC,∴四边形AECF是菱形.
(2)解:设AF=x.
∵EF是AC的垂直平分线,∴AF=CF=x.
∴BF=8-x.
在Rt△ABF中,由勾股定理得: AB2+BF2=AF2,
即42+(8-x)2=x2,解得x=5.
∴AF=5.
∴菱形AECF的周长为4×5=20.
23.解:(1)BF=DE.证明如下:
∵四边形ABCD是正方形,
∴AB=AD,∠DAC=∠BAC=45°.
∵AF⊥AC,∴∠BAF=∠BAC=∠DAC=45°.
又∵AB=AD,AF=AE.
∴△AFB≌△AED(SAS).
∴BF=DE.
(2)四边形AFBE是正方形.证明如下:
∵四边形ABCD是正方形,E是AC的中点,∴AE=BE.
在△ABF和△ABE中,
∴△ABF≌△ABE(SAS).
∴BF=BE.
∴AE=BE=BF=AF.
∴四边形AFBE是菱形.
又∵AF⊥AE,∴四边形AFBE是正方形.
24.解:(1)AB=CG-CE.证明如下:
∵四边形ABCD是菱形,∴AB=BC.
又∵∠BAC=60°,∴△ABC是等边三角形.
∴AB=AC.
∵∠EAG=60°,∴∠BAC=∠EAG.
∴∠BAC+∠CAE=∠EAG+∠CAE,
即∠BAE=∠CAG.
又∵四边形AEFG是菱形,
∴AE=AG.
在△ABE和△ACG中,
∴△ABE≌△ACG(SAS).
∴BE=CG.
∵AB=BC=BE-CE,
∴AB=CG-CE.
(2)AB=CE-CG.
