2022届高三信息技术选考总复习专题25 对分查找 课件(66张PPT)
文档属性
| 名称 | 2022届高三信息技术选考总复习专题25 对分查找 课件(66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 490.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-10-31 22:31:39 | ||
图片预览










文档简介
(共66张PPT)
专题25 对分查找
一、基本算法思想
1.在一个____序或____序的数组中,确定该数组的开始位置i、结束位置j和中间位置m,用待查找的数key与m位置所在的值a(m)比较,如果相等,表示找到了。如果中间位置的数a(m)不是要查找的数,把区间分为[________]和[________]两部分。如果在前半段,把结束位置____修改为________,再次查找;如果在后半段,把开始位置____修改为________,再次查找,直到找到或者开始位置大于结束位置为止。
2.中间位置m的计算公式:①m=Int((i+j)/2)或者m=(i+j)\'2或者m=fix((i+j)/2);②m=Int((i+j+1)/2);③m=Int(Rnd*(j-i+1)+i)
3.变量i和j分别表示搜索的开始和结束区间,当变量i=j时,该区间是只有一个数据,当要查找的数不在区间中,接着要么i往后移,要么j往前移,因此必定有i>j或i=j+1的结论。
升
降
i,m-1
m+1,j
m-1
i
m+1
j
二、查找过程
1.明确i、j和m的含义,i表示开始位置,j表示结束位置,____表示[i,j]的中间位置。______表示m这个位置所对应的数值。
2.修改i、j的值,如果是升序系列,当要查找的数比中间的数a(m)____ ,表示要查找的数在前半段,执行语句___________;否则在后半段,执行语句___________。如果是降序系列,则相反。
3.结束查找有两个条件,中间m位置值a(m)与要查找的数key相等,或者是头指针____已经大于尾指针____。满足其中一个条件,分别表示找到了或者没有找到,就不再查找了。
4.查找结束后,查找的结论是要查找的数在数组中位置____或者______找到。
m
d(m)
小
j=m-1
i=m+1
i
j
m
没有
三、N个数最多的查找次数
N个数最多的查找次数最少的查找次数为_____________,最多的查找次数为________________。可以使用后面二叉树知识进行解释。
四、常用解题技巧
若题目是要查找的数key已知,采用________比较快;若key未知,或是一个范围内的数,采用________法解题比较有效。
1.列表法
用表格列出每次查找数组d的区间开始位置i、j和比较数的位置____及值______。模拟对分查找的过程。
Int(Log2N)
Int(Log2N)+1
列表法
二叉树
m
a(m)
2.二叉树法
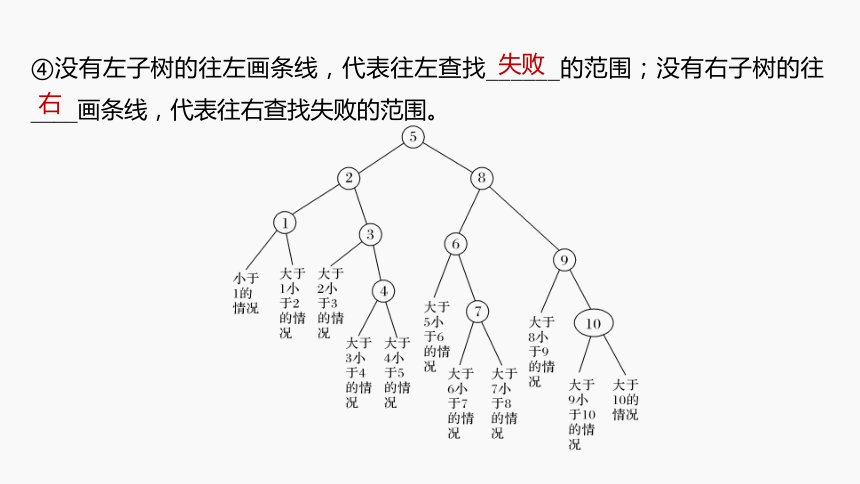
二叉树分为根结点和叶子结点,这些结点都是每次查找的位置m或值a(m),一个根结点最多有左右两个孩子,叶子结点是查找不成功时,最后一次查找的中点位置m。
①假设有10个数据1、2、3、4、5、6、7、8、9、10取m=(i+j)\2值为根节点,然后分成左右2堆数据放入左右2个子树;
②右2堆依次求出m值(2、8),m值保留在原位,然后把2边数分别放入它的左右2个子树(小的放左子树,大的放右子树);
③节点里还有2个及以上数的,按照上面规则求m值,m值保留在原位,其他数放入它的左右2个子树(小的放左子树,大的放右子树);
④没有左子树的往左画条线,代表往左查找______的范围;没有右子树的往____画条线,代表往右查找失败的范围。
失败
右
⑤每层最多的根结点和叶子结点数之和
第1,2,3,4层的叶子结点数分别为1,2,4,8,可以得到规律,第n层的叶子结点数为__________,第n层最多的根结点和叶子结点数之和:首项为1,等比为____的前____项之和,即2^n-1。
⑥当查找根结点时,还可以继续查找,因此查找不成功一定发生在______结点。
2^(n-1)
2
n
叶子
⑦在程序代码中,语句If key<=a(m) Then j=m-1 Else i=m+1,表示当key=a(m)时,还要执行j=m-1,即找到要找的数,继续向左查找,当一个系列中有相等的数时,查找最左边的数。查找结束的唯一条件是i>j,即i=j+1。因此可以根据最后一次移动区间左边界或右边界,判断程序运行后的变量i和j的值。数组元素a(1)到a(10)依次为2,3,7,9,10,11,15,15,19,21,以在数组中查找5,9,15为例。查找5时,若m的计算公式为(i+j)\2,先找到2号位置的数值,若m的计算公式为(i+j+1)\2,先找到3号位置的数值。当找到2号位置值3,还要移动左边界i,因此i=m+1,即i=3,j=2。或者找到3号位置7,还要移动右边界j,因此j=m-1,即j=2,i=3。查找9或15时,找到后,还要移动右边界j,j的值为m-1,因此最后要找数的位置在i的位置。
考点一 采用列表法模拟算法思想
当key已知时,可以列表法依次找出i、j、m和a(m)的值,进行变量跟踪。
【例1】 某二分查找算法的VB程序段如下:
Key=Val(Text1.Text)
i=1: j=9
Text2.Text=””
Do While i <=j
If Key=a(m) Then Exit Do
If Keyi=m+1
Else
A
j=m-1
End If
Text2.Text=Text2.Text+” ”+Str(a(m))
Loop
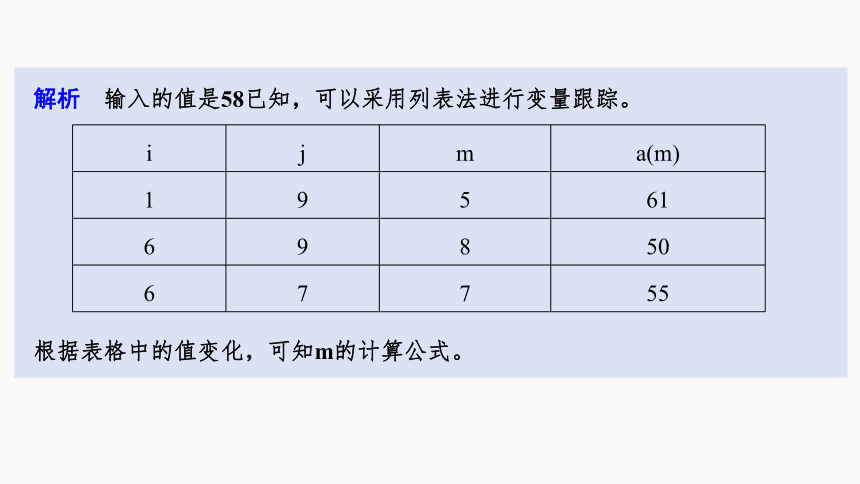
数组元素a(1)到a(9)的值依次为88,75,70,68,61,58,55,50,43,文本框Text1中输入的值是58,执行该程序段,文本框Text2中显示的是61,50,55,则方框处的代码应为( )
A.m=(i+j+1)\2 B.m=(i+j)\2+1
C.m=(i+j)\2 D.m=(i+j-1)\2
解析 输入的值是58已知,可以采用列表法进行变量跟踪。
i j m a(m)
1 9 5 61
6 9 8 50
6 7 7 55
根据表格中的值变化,可知m的计算公式。
B
【变式1】 某对分查找算法的 VB 程序段如下:
i=1: j=6: n=0: f=False
Key=Val(Text1.Text)
Do While i <=j And Not f
n=n+1
m=Fix((i+j)/2)
If Key=a(m) Then f=True
If KeyLoop
数组元素 a(1)到 a(6)的值依次为“12,19,27,31,46,55”。文本框Text1中输入“30”后运行该程序,则以上程序段运行结束后,下列说法不正确的是( )
A.变量 i 的值为 4 B.变量 j 的值为 5
C.变量 m 的值为 4 D.变量 n 的值为 3
解析 本题考核的知识点是对分查找。可以用列表法进行跟踪变量。
i j m a(m) n flag
1 6 3 27 1 False
4 6 5 46 2 False
4 4 4 31 3 False
4 3
当i>j时,不再查找。
考点二 对分查找的算法思想实现
在一个[i,j]区间内,先确定一个中间位置m,判断m位置上的值是否是要查找的数,如果不是,移动变量i或j的值,缩小[i,j]的边界,直到找到该数(找到返回位置)或区间不存在(变量i>j,未找到,退出查找)。中间位置m指在区间[i,j]中间的任意位置,通过有m=(i+j)\2或m=(i+j+1)\2或m=Int(Rnd*(j-i+1))+i三种计算公式。
【例2】 数组a中存储的是左右交替上升的n个正整数,如下表所示:
a(1) a(2) a(3) …… a(n-2) a(n-1) a(n)
3 25 38 …… 55 31 12
依据对分查找思想,设计一个在数组a中查找数据key的程序,实现该功能的VB程序如下,但加框处代码有错,请改正。
Private Sub Command1_Click()
Const n=6
Dim a(1 To n) As Integer,flag As Boolean
Dim i As Integer,j As Integer,m As Integer,key As Integer
′读取一组正整数,按上述规则存入数组a中,代码略
key=Val(Text1.Text)
i=1
j=(n+1)\2
flag=False
m=(i+j)\2
If key=a(m) Then
flag=True
ElseIf keyj=m-1
Else
i=m+1
End If
Loop
If Not flag And j>0 Then
If key=a(m) Then flag=True
End If
If flag Then Text2.Text=Str(m) Else Text2.Text=”找不到”
End Sub
答案 (1)i<=j (2)n-i+2 或n-j+1 或n+1-(i+j)
解析 本题考核对分查找的思想,算法比较简单,关键是对数组a中存储的是左右交替上升的n个正整数的理解,数组的前半部分是递增的,后半部分是递减的,且他们的大小变化规律是3→12→25→31→38→55。因此如果在前半部分找不到,还可能在右半部分对称的位置找到。因此(1)应修改为i<=j,也就是说最后一次查找,变量i=j=m。如果在前半部分找不到,该数可能比a(m)小,此时j=m-1,该数大于(j)但小于a(m),在与j对称的位置(即n-j+1)可能是要找的数;该数可能比a(m)大,此时i=m+1,该数大于a(m)但小于a(i),在与(i-1)对称的位置(即n-(i-1)+1)可能是要找的数。
【例3】 有如下VB程序段:
i=1: j=6: s=””
Key=Val(Text1.Text)
Randomize
Do While i <=j
M=Int(Rnd*(j-i+1)+i)
If a(M)j=M-1
ElseIf a(M)>Key Then
i=M+1
Else
Exit Do
End If
Loop
D
数组元素a(1)到a(6)的值依次为“88、72、53、29、24、12”,文本框Text1中输入的值是24,执行该程序段,下列查找顺序不可能出现的是( )
A.12 53 24 B.72 53 29 12 24
C.53 12 29 24 D.53 12 72 24
解析 表达式Int(Rnd*(j-i+1))的最大值为j-i,因此m的取值范围是[i,j]之间的一个数。对分查找是在一个区间[i,j]内进行查找中间位置m对应的数值a(m),若a(m)<>key,则j移动到前面区间[1,m-1]或i移动到[m+1,j]再次进行查找。A选项中,第2、3、4次查找的区间是依次是[1,5]、[4,5]、[5,5];B选项查找的区间依次是[1,6]、[3,6]、[4,6]、[4,5]、[5,5];C选项查找的区间依次是[1,6]、[4,6]、[4,5]、[5,5];D选项查找的区间依次是[1,6]、[4,6]、[4,5],而第3个数72不可能在区间[4,5]中。
【变式2】 已知直角三角形的斜边长度Key,利用对分查找算法计算其他两条整数边长的VB程序段如下:
flag=True : p=0
Key=5
For i=1 To Key-1
L=i
____①____
Do While____②____
M=(L+R)\2
p=p+1
If i*i+M*M L=M+1
ElseIf i*i+M*M>Key*Key Then
R=M-1
Else
A
Text2.Text=Str(i)+” ”+Str(M)+” ”+Str(Key)
flag=False
i=Key
End If
Loop
Next i
If flag Then Text2.Text=”没有符合条件的整数勾股数对!”
上述程序段2个划线处的代码分别为( )
A.①R=Key-1 ②L<=R And flag
B.①R=Key ②L<=R And flag
C.①R=Key-1 ②L<=R Or flag
D.①R=Key-1 ②L<=R And flag=False
解析 L和R表示两条直角边长,R只能比斜边短。Flag表示是否找到的标志。
【变式3】 (2021·1月浙江选考)某对分查找算法的VB程序段如下:
′随机产生包含20个整型元素的升序序列,依次存入数组a,代码略
i=1:j=20:s=””
key=Val(Text1.Text)
Do While i<=j
m=(i+j)\2
s=s+Str(a(m))
If a(m)=key Then Exit Do ′Exit Do表示退出循环
If a(m)>key Then j=m-1 Else i=m+1
Loop
Text2.Text=s
C
在文本框Text1中输入待查找数,执行该程序段后,下列选项中,文本框Text2中显示的内容不可能的是( )
A.78 50 46 33 B.51 37 41 48
C.74 50 46 51 D.73 83 87 89
解析 考查了对分查找的识读。选项C:按照对分查找的特点,当找到50后,往左找到46,后面不会再找到大于50的数字,选项错误。
【变式4】 若数组元素a(1)到a(8)的值依次为“6,9,12,18,20,28,32,45”,查找key值的VB程序段:
i=1: j=8: c=0
Do While i <=j
Randomize
m=Int(Rnd*(j-i+1))+i
If Key=a(m) Then ExitDo
If a(m)>Key Then
j=m-1
c=c+1
Else
i=m+1
c=c-1
End If
Loop
A
若查找的key值为18,运行该段程序后,下列说法正确的是( )
A.c的值可能为0 B.j=m-1 至少要执行一次
C.程序结束时i>j D.i的值可能为5
解析 m是i到j之间的一个随机位置,当第一次产生m的值为4,找到要找到的数,此时c等于0,语句j=m-1可能没有被执行到。由于要查找的key值是存在的,产生的m小于4,将改为i为m+1,生产的m大于4,将改为j为m-1,即查找的区间左右边界不断地靠近4,即i不可能超过4,j的值不可能小于4,因此肯定在查找过程中退出循环,因此i<=j。
考点三 采用二叉树法模拟算法思想
在查找一个数的路径中,可以确定每次查找的数位置和值,可以判断查找次数,若找不到该数据时,可以判断此时变量i、j和m的值。大致可以分为以下几种情况:①随机给出查找值,求查找次数或查找路径;②给出查找次数或查找路径,求查找值的范围;③当查找成功时没有结束查找,求查找次数或查找的边界值。
【例4】 有如下VB程序段:
c=0: i=1: j=9
f=False
Key=Val(Text1.Text)
Do While i <=j And Not f
m=(i+j+1)\2
c=c+1
If Key=d(m) Then
f=True
ElseIf Key>d(m) Then
j=m-1
Else
i=m+1
End If
Loop
D
数据元素d(1)到d(9)的值依次为“98,85,71,54,37,30,24,15,9”,若运行该程序段后c的值为4,则Text1中输入的值不可能为( )
A.30或31 B.88或98 C.30或28 D.9或54
解析 由于要查找的key值未知,可以用二叉树法解题,但要注意m的计算方法。由图可知,能找到的情况是输入的第1或第6个数。找不到的情况是比第1个数大,或比第1个数但比第2个数大,或者比第5个数小,但比第6个数小,或者比第6个数大,但比第7个数小。
【例5】 某算法的VB程序段如下:
i=1: j=7: s=””
key=Int(Rnd*100)
Do While i <=j
m=(i+j)\2
If Key=a(m) Then
s=s+”M”: Exit Do
ElseIf Keyj=m-1: s=s+”L”
Else
i=m+1: s=s+”R”
End If
Loop
Text1.Text=s
C
数组元素a(1)到a(7)的值依次为“24,35,38,41,45,69,78”。执行该程序段后,文本框Text1中显示内容可能的是( )
A.RL B.LMR C.RLR D.LRLM
解析 第一次查找的位置是4,数值为41,此
时可能有三种处理结果,相等输出M,退出;
比41小,变量j左移,继续查找;比41大,变
量i右移,继续查找。以查找37、38和39为例,
先依次访问41和35,接着访问38,查找38的结
果是LRM,查找37的结果是LRL,查找39的结果是LRR。因此选项A只找到第二个结点,若找到了,则输出M,否则还可以向左或向右继续查找。选项B在找到情况下,不可能再次查找。选项C查找比第5个数大,但比第6个数小的数。选项D中LRL表示查找比第3个数大但比第4个数小的数,因此不可能再次找到。
【变式5】 对分查找程序如下:
i=1: j=15: n=0: Key=Val(Text1.Text)
Do While i <=j
m=(i+j)\2
If a(m)=Key Then
Exit Do
ElseIf a(m)>Key Then
j=m-1: n=n-1
Else
i=m+1: n=n+1
End If
Loop
B
执行该程序段后,n的值为-3,则下列说法正确的是( )
A.该程序若要实现对分查找,要求数组a按降序排列
B.查找key的值可能等于a(1)元素的值
C.查找key的值可能小于a(1)元素的值
D.查找key的值可能大于a(15)元素的值
解析 当条件a(m)>Key成立时,指针j=m-1,因此该数组是升序排列的。15个数,最多查找4次,n的值为-3,说明一直向左继续查找。找到结点8,4,2,1时的n值分别是0,-1,-2,-3,因此找到的数可能是a(1),若小于a(1)元素的值,n的值为-4,可能大于a(15)元素,n的值为4。
【变式6】 某算法程序段如下:
i=1: j=10: n=0
key=Int(Rnd*10)*2+1
Do While i <=j
m=Int((i+j)/2+0.5)
If key=a(m) Then
Exit Do
ElseIf key>a(m) Then
j=m-1: n=n-1
Else
i=m+1: n=n+1
End If
Loop
Text1.Text=Str(n)
A
已知数组元素 a(1)至 a(10)的值依次为 20,19,17,16,14,11,8,5,2,0若执行该程序后,文本框 Text1中显示的内容不可能是( )
A.-3 B.-2 C.-1 D.1
解析 key的值在1-19之间的奇数。采用二叉树法进行解题,当找到11时,n的值为0。当找到17时,n的值为-1,当找到19时,n的值为-2,19已经是要产生的key中最大值。若要查找的数7,则n的值为1。
C
【变式7】 某对分查找算法的 VB 程序段如下:
′数组元素f(1)到 f(9)赋初值为 0,代码略
Key=Val(Text1.Text):
i=1: j=9
Do While i <=j
m=(i+j)\2
f(m)=1
If a(m)=Key Then Exit Do ′Exit Do 表示退出循环
If a(m)>Key Then j=m-1 Else i=m+1
Loop
整型数组元素 a(1)到 a(9)为升序序列,在文本框 Text1 中输入待查找数,执行该程序段后,下列选项中,f(1)到 f(9)各元素值不可能的是( )
A.1,1,0,0,1,0,0,0,0 B.0,0,0,0,1,0,0,0,0
C.0,0,0,0,1,1,1,1,0 D.0,1,1,1,1,0,0,0,0
解析 本题对分查找算法。通过构建二叉树,
A选项访问的中间分别为 5、2、1,B选项若 key=a(5)时,查找一次,循环中途退出。D选项访问的中间分别为 5、2、3、4。
【例6】 (2020·5月柯桥)有如下VB程序段:
low=1: high=8
Key=Val(Text1.Text)
Do While low <=high
m=(low+high)\2
If a(m)>=Key Then
high=m-1
Else
low=m+1
End If
Loop
D
数组元素a(1)至a(8)中的分别为5,7,12,12,15,20,25,27,执行该程序段后,变量low的值为3,则文本框Text1中输入的值不可能是( )
A.10 B.11 C.12 D.13
解析 由于输入的值不知,因此可以采用二叉树来解决问题。当输入12时,找到了但未退出,而是向左查找,因此依次查找12、7和12,当找到12时,high=2,low=3,退出循环。输入10和11时,与访问12有路径是相同的。查找13时,依次查找12、20和15,low=5。
【变式8】 (2020·9月A9协作体)某对分查找算法的 VB程序段如下:
Key=Val(Text1.Text): s=””
i=1: j=10
Do While i <=j
m=(i+j)\2
If a(m)>Key Then
i=m+1
s=s+”R”
Else
j=m-1
s=s+”L”
End If
Loop
Text2.Text=s
B
数组元素a(1)到a(10)的值依次为“33,21,18,14,14,14,10,6,4,1”。在文本框Text1中输入14后,该程序段的输出结果与输入下列值的输出结果相同的是( )
A.10 B.16 C.19 D.3
解析 在查找过程中,若找到要找的数值key,没有结束查找,而是向左继续查找。画出二叉树,如图所示。最后一次查找第4个位置,且向左查找,因此只要查找的数介于第3和第4个之间的数,输出结果都是一样的。
【变式9】 (2020·9月之江教育)有如下VB程序段:
Dim a(1 To 8) As Integer
Dim i As Integer,j As Integer,m As Integer,k As Integer
i=1: j=8
a(1)=87: a(2)=66: a(3)=59: a(4)=40
a(5)=39: a(6)=30: a(7)=22: a(8)=13
k=Val(Text1.Text)
Do While i <=j
m=(j+i+1)\2
If a(m)Loop
Text2.Text=Str(i)
A
程序执行完后,i的值是4,则k的值不可能是( )
A.40 B.41 C.48 D.59
解析 由于查找的值未知,因此往往采用二叉树法解题。
A选项找到第4个数40,还要向右查找,因此i的值为5。
B和C选项该数介于第3个和第4个数之间,找到第4个数后,改变j的值,向左查找。
D选项,当查找的k找到后,还要向右查找,此时i大于j。
【变式10】 下列VB程序段功能为:在升序排序数组a中(a(1)≤a(2)≤a(3)……)采用对分查找的方式查找某数值,若能找到,则输出该数值在数组a中的起始和结束位置,否则输出“找不到”。
Dim a(0 To 10) As Integer
Key=Val(Text1.Text)
i=1: j=10
Do While i <=j
m=(i+j)\2
If____①____ Then
j=m-1
E1se
i=m+1
End If
Loop
If a(j) <>Key Then
Label1.Caption=”找不到”
Else
p1=j
Do While Key=a(j) And j>=1
j=j-1
Loop
____②____
Label1.Caption=Str(p2)+”-”+Str(p1)
End If
程序划线处的代码应为( )
A.①keyC.①key<=a(m) ②p2=j D.①key<=a(n) ②p2=j+1
B
解析 从输出语句来看,p2和p1为该数值在数组a中的起始和结束位置,p1的初值为j,因此j是右极限位置,即当a(m)=key时,还要将i赋值为m+1,继续向右查找。从j的位置一直往前找,当条件Key=a(j)不成立时,j已经不再指向key了,最后一个等于key的位置是j+1。
【例7】 有如下VB程序段:
i=1: j=8: n=0: s=””
key=2
Do While i <=j
m=Int(Rnd*(j-i+1))+i
n=n+l: s=s+Str(m)
If a(m)=Key Then Label1.Caption=”找到第”+Str(m)+”个”
If Key>a(m) Then i=m+1 Else j=m-1
Loop
Label1.Caption=s
A
若数组a(1)~a(8)的值依次为“1,2,2,2,2,6,6,8”,程序段运行后,下列说法正确的是( )
A.m的值可能分别为3 2 1 B.m的值一定为2
C.找到第5个位置上的2 D.n的值可能为1
解析 m随机值在区间[i,j]内,由于循环中间没有执行退出,所以最后循环结束必然i大于j,并且i=j+1, 循环过程中key>a(m),向右缩减区间, key<=a(m),向左缩减区间,最后j一定会走到首个key位置的左边,此时i指向这个key,即第一个2,循环结束,最后i=2,j=1,而m取值可能为2,也可能是1。
1.某对分查找算法的VB程序段如下:
D
flag=False
i=0:j=6:c=0
Do While i <=j And flag=False
m=Fix((i+j)/2+0.5)
If Key=a(m) Then flag=True
If Keyc=c+1
Loop
数组元素a(0)到a(6)的值依次为“3,12,30,46,69,72,84”,Key的值为84。若该程序段执行后,以下说法中正确的是( )
A.i=6 B.j=7 C.m=7 D.c=3
解析 本题可以采用列表法解题,但要注意m的计算公式。当找到key时,并没有马上退出,而是执行了下一条IF语句,因此i的值为7。
i j m a(m)
0 6 3 46
4 6 5 72
6 6 6 84
2.数组a中依次存放6个有序数据“23 33 44 55 66 77”。
D
i=1: j=6: c=0: Key=35
Do While i <=j
c=c+1
m=(i+j)\2
If (j-i+1) Mod 2=0 Then m=m+1
If a(m)=Key Then Exit Do
If KeyLoop
该程序段运行后,下列各变量的值不正确的是( )
A.i=3 B.j=2 C.c=3 D.m=2
解析 本题可以采用列表法解题。
i j m a(m)
1 6 4 55
1 3 2 33
3 3 3 44
3 2
3.(2019·12月新力量联考)某对分查找算法的VB程序段如下:
Const n=100: Dim d(1 To 100) As Integer
For i=1 To 100
d(i)=i
Next i
Key=300
For i=1 To n-1
L=i+1: R=n
Do While L <=R
m=(L+R)\2
If d(i)*d(m) L=m+1
ElseIf d(i)*d(m)>Key Then
R=m-1
Else
Label1.Caption=Str(d(i))+” ”+Str(d(m))
Exit Do
End If
Loop
Next i
If Label1.Caption=”” Then Label1.Caption=”没有符合的数对”
该程序段执行后,标签Label1中显示的内容是( )
A.3 100 B.15 20 C.50 6 D.没有符合的数对
解析 在[i+1,100]之间查找一个数,该数与i乘积等于300,注意两个要点,该数大于i且小于100。最小的数对为3和100,因此最大的数对为15和20,虽然50*6=300,但不符合大于i的条件。
B
4.(2019·12月稽阳)有如下 VB 程序:
a(1)=1
For i=2 To 12
a(i)=a(i-1)+Int(Rnd*2)+1
Next i
Key=Val(Text1.Text)
i=1: j=12: cnt=0: flag=False
Do While i <=j And flag=False
cnt=cnt+1
m=(i+j+1)\2
If a(m)=Key Then
flag=True
ElseIf Key>a(m) Then
i=m+1
Else
j=m-1
End If
Loop
程序运行后,下列说法正确的是( )
A.在Text1输入15,程序运行后m肯定为12
B.在Text1输入6,程序运行后cnt可能大于3
C.若查找不成功,则j>m肯定成立
D.若查找不成功,则i<=m肯定成立
B
解析 在第1个For语句中,可以得知,数组a中,从第2个数开始肯定比前面的数至少大1,因此a(12)的最小可能是12,最大可能是23。数15最大的位置可能在12,最小的位置可能是8,因此m的值在8~12均有可能。数6最大位置可能是6,最小位置可能是4,可以对左面半边进行分析,若查找的数在第4个位置,或者比第4个位置大,但比第5个位置小,均要查找3次。若查找不成功,j可能等于m-1,i有可能=m+1。
5.(2019·10月五校联考)某对分查找算法的 VB 程序段如下:
Key=Int(Rnd*49)*2+1
s=0: i=1: j=10
Do While i <=j
m=(i+j)\2
If Key=a(m) Then Exit Do
If Keyj=m-1: s=2*s
Else
i=m+1: s=2*s+1
End If
Loop
数组 a(1)到 a(10)的值依次为“2,6,7,15,20,24,27,43,52,63”,执行该程序段后,s 的值不可能为( )
A.2 B.3 C.5 D.15
解析 本题考核的是对分查找的算法。要查找的数在1至97之间的奇数。查找一次找到了,s等于0。第2次如果在左区间查找,s=0;在右区间查找并找到,s=1。第2次在右区间中查找不成功,继续向左查找,即找到第6个数,则s=2,但第6个数为偶数。向右查找,则s=3。可以使用二叉树法来解题。查找到第3个节点时,s=1,继续向左查找,s=2,该数范围在第2个节点和第3个节点之间,即[6,7]之间,该区间中没有整数,因此不可能。
A
6.某对分査找算法的VB程序段如下:
i=1: j=7: s=””:key=3
Do While i <=j
m=(i+j)\2
If key=a(m) Then s=s+”M”
If key j=m-1: s=s+”L”
Else
i=m+1: s=s+”R”
End If
Loop
Text1.Text=s
C
数组元素a(1)到a(7)的值依次为“1,2,3,3,3,5,8”。若该程序段执行后,文本框Text1中显示的内容是( )
A.MRMR B.MLMR C.MRLMR D.LRLM
解析 查找过程中不断输出key与m位置的值进行比较,若相等则输出“M”但并没有结束查找,接着执行第二个选择结构,继续向右移动。访问中点m的值依次为4,6,5,此时i和j的值均等于5,i继续向右移动,条件i<=j不成立,退出循环。在结点4和5分别输出两个字母,且都为MR,因此文本框中输出MRLMR。
C
7.某算法的VB程序段如下:
key=Int(Rnd*5)*2+11
i=1:j=8:c=0
Do While i<=j
m=(i+j+1)\2
If a(m)>=key Then i=m+1 Else j=m-1
c=c+1
Loop
数组元素a(1)到a(8)的值依次为“23,21,19,18,16,15,14,11”。 若该程序段执行后,下列说法错误的是( )
A.i的值为j+1 B.i的值可能是9
C.j的值可能是5 D.c的值一定是3
解析 产生key值的范围是11至19之间的奇数,
即只能产生在第3个到第8个之间的数。程序代
码中,找到key时,并没有退出查找,而是向右
继续查找,因此退出循环时,肯定满足条件i>j,
即i=j+1。画出二叉树如图所示。若i要达到最大值,则必须一直向右查找,当要找的数是11时,i达到极值9,此时j=m=8,查找结束。从图中可知,当找到a(5),a(3),a(7)时并没有结束查找,因此必须要查找3次才能退出。j的值若要为5,则查找的数比a(5)小但比a(6)大,但a(5)和a(6)之间没有相应的奇数。
8.某对分查找算法的 VB 程序段如下:
n=0: i=l: j=8
Key=Val(Text1.Text)
Do While i <=j
m=(i+j)\2
n=n+1
If Key=d(m) Then Exit Do
If Key>d(m) Then j=m-1 Else i=m+1
Loop
If i <=j Then s=Str(m-n) Else s=Str(n)
B
数组元素d(1)到d(8)的值依次为“87,75,50,44,36,24,15,8”,输入某个key值,运行该程序段后,变量s结果为2,则输入key的值是( )
A.75 B.36 C.24 D.15
解析 由于输入key未知,可以采用二叉树法。变量n表示查找次数,m表示找到值的结点。若找到该数,s的值为m-n,若没有找到值为n。查找2次,显然不可能是没有找到。输入key的值为36,m的值为5,找了3次。
专题25 对分查找
一、基本算法思想
1.在一个____序或____序的数组中,确定该数组的开始位置i、结束位置j和中间位置m,用待查找的数key与m位置所在的值a(m)比较,如果相等,表示找到了。如果中间位置的数a(m)不是要查找的数,把区间分为[________]和[________]两部分。如果在前半段,把结束位置____修改为________,再次查找;如果在后半段,把开始位置____修改为________,再次查找,直到找到或者开始位置大于结束位置为止。
2.中间位置m的计算公式:①m=Int((i+j)/2)或者m=(i+j)\'2或者m=fix((i+j)/2);②m=Int((i+j+1)/2);③m=Int(Rnd*(j-i+1)+i)
3.变量i和j分别表示搜索的开始和结束区间,当变量i=j时,该区间是只有一个数据,当要查找的数不在区间中,接着要么i往后移,要么j往前移,因此必定有i>j或i=j+1的结论。
升
降
i,m-1
m+1,j
m-1
i
m+1
j
二、查找过程
1.明确i、j和m的含义,i表示开始位置,j表示结束位置,____表示[i,j]的中间位置。______表示m这个位置所对应的数值。
2.修改i、j的值,如果是升序系列,当要查找的数比中间的数a(m)____ ,表示要查找的数在前半段,执行语句___________;否则在后半段,执行语句___________。如果是降序系列,则相反。
3.结束查找有两个条件,中间m位置值a(m)与要查找的数key相等,或者是头指针____已经大于尾指针____。满足其中一个条件,分别表示找到了或者没有找到,就不再查找了。
4.查找结束后,查找的结论是要查找的数在数组中位置____或者______找到。
m
d(m)
小
j=m-1
i=m+1
i
j
m
没有
三、N个数最多的查找次数
N个数最多的查找次数最少的查找次数为_____________,最多的查找次数为________________。可以使用后面二叉树知识进行解释。
四、常用解题技巧
若题目是要查找的数key已知,采用________比较快;若key未知,或是一个范围内的数,采用________法解题比较有效。
1.列表法
用表格列出每次查找数组d的区间开始位置i、j和比较数的位置____及值______。模拟对分查找的过程。
Int(Log2N)
Int(Log2N)+1
列表法
二叉树
m
a(m)
2.二叉树法
二叉树分为根结点和叶子结点,这些结点都是每次查找的位置m或值a(m),一个根结点最多有左右两个孩子,叶子结点是查找不成功时,最后一次查找的中点位置m。
①假设有10个数据1、2、3、4、5、6、7、8、9、10取m=(i+j)\2值为根节点,然后分成左右2堆数据放入左右2个子树;
②右2堆依次求出m值(2、8),m值保留在原位,然后把2边数分别放入它的左右2个子树(小的放左子树,大的放右子树);
③节点里还有2个及以上数的,按照上面规则求m值,m值保留在原位,其他数放入它的左右2个子树(小的放左子树,大的放右子树);
④没有左子树的往左画条线,代表往左查找______的范围;没有右子树的往____画条线,代表往右查找失败的范围。
失败
右
⑤每层最多的根结点和叶子结点数之和
第1,2,3,4层的叶子结点数分别为1,2,4,8,可以得到规律,第n层的叶子结点数为__________,第n层最多的根结点和叶子结点数之和:首项为1,等比为____的前____项之和,即2^n-1。
⑥当查找根结点时,还可以继续查找,因此查找不成功一定发生在______结点。
2^(n-1)
2
n
叶子
⑦在程序代码中,语句If key<=a(m) Then j=m-1 Else i=m+1,表示当key=a(m)时,还要执行j=m-1,即找到要找的数,继续向左查找,当一个系列中有相等的数时,查找最左边的数。查找结束的唯一条件是i>j,即i=j+1。因此可以根据最后一次移动区间左边界或右边界,判断程序运行后的变量i和j的值。数组元素a(1)到a(10)依次为2,3,7,9,10,11,15,15,19,21,以在数组中查找5,9,15为例。查找5时,若m的计算公式为(i+j)\2,先找到2号位置的数值,若m的计算公式为(i+j+1)\2,先找到3号位置的数值。当找到2号位置值3,还要移动左边界i,因此i=m+1,即i=3,j=2。或者找到3号位置7,还要移动右边界j,因此j=m-1,即j=2,i=3。查找9或15时,找到后,还要移动右边界j,j的值为m-1,因此最后要找数的位置在i的位置。
考点一 采用列表法模拟算法思想
当key已知时,可以列表法依次找出i、j、m和a(m)的值,进行变量跟踪。
【例1】 某二分查找算法的VB程序段如下:
Key=Val(Text1.Text)
i=1: j=9
Text2.Text=””
Do While i <=j
If Key=a(m) Then Exit Do
If Key
Else
A
j=m-1
End If
Text2.Text=Text2.Text+” ”+Str(a(m))
Loop
数组元素a(1)到a(9)的值依次为88,75,70,68,61,58,55,50,43,文本框Text1中输入的值是58,执行该程序段,文本框Text2中显示的是61,50,55,则方框处的代码应为( )
A.m=(i+j+1)\2 B.m=(i+j)\2+1
C.m=(i+j)\2 D.m=(i+j-1)\2
解析 输入的值是58已知,可以采用列表法进行变量跟踪。
i j m a(m)
1 9 5 61
6 9 8 50
6 7 7 55
根据表格中的值变化,可知m的计算公式。
B
【变式1】 某对分查找算法的 VB 程序段如下:
i=1: j=6: n=0: f=False
Key=Val(Text1.Text)
Do While i <=j And Not f
n=n+1
m=Fix((i+j)/2)
If Key=a(m) Then f=True
If Key
数组元素 a(1)到 a(6)的值依次为“12,19,27,31,46,55”。文本框Text1中输入“30”后运行该程序,则以上程序段运行结束后,下列说法不正确的是( )
A.变量 i 的值为 4 B.变量 j 的值为 5
C.变量 m 的值为 4 D.变量 n 的值为 3
解析 本题考核的知识点是对分查找。可以用列表法进行跟踪变量。
i j m a(m) n flag
1 6 3 27 1 False
4 6 5 46 2 False
4 4 4 31 3 False
4 3
当i>j时,不再查找。
考点二 对分查找的算法思想实现
在一个[i,j]区间内,先确定一个中间位置m,判断m位置上的值是否是要查找的数,如果不是,移动变量i或j的值,缩小[i,j]的边界,直到找到该数(找到返回位置)或区间不存在(变量i>j,未找到,退出查找)。中间位置m指在区间[i,j]中间的任意位置,通过有m=(i+j)\2或m=(i+j+1)\2或m=Int(Rnd*(j-i+1))+i三种计算公式。
【例2】 数组a中存储的是左右交替上升的n个正整数,如下表所示:
a(1) a(2) a(3) …… a(n-2) a(n-1) a(n)
3 25 38 …… 55 31 12
依据对分查找思想,设计一个在数组a中查找数据key的程序,实现该功能的VB程序如下,但加框处代码有错,请改正。
Private Sub Command1_Click()
Const n=6
Dim a(1 To n) As Integer,flag As Boolean
Dim i As Integer,j As Integer,m As Integer,key As Integer
′读取一组正整数,按上述规则存入数组a中,代码略
key=Val(Text1.Text)
i=1
j=(n+1)\2
flag=False
m=(i+j)\2
If key=a(m) Then
flag=True
ElseIf key
Else
i=m+1
End If
Loop
If Not flag And j>0 Then
If key=a(m) Then flag=True
End If
If flag Then Text2.Text=Str(m) Else Text2.Text=”找不到”
End Sub
答案 (1)i<=j (2)n-i+2 或n-j+1 或n+1-(i+j)
解析 本题考核对分查找的思想,算法比较简单,关键是对数组a中存储的是左右交替上升的n个正整数的理解,数组的前半部分是递增的,后半部分是递减的,且他们的大小变化规律是3→12→25→31→38→55。因此如果在前半部分找不到,还可能在右半部分对称的位置找到。因此(1)应修改为i<=j,也就是说最后一次查找,变量i=j=m。如果在前半部分找不到,该数可能比a(m)小,此时j=m-1,该数大于(j)但小于a(m),在与j对称的位置(即n-j+1)可能是要找的数;该数可能比a(m)大,此时i=m+1,该数大于a(m)但小于a(i),在与(i-1)对称的位置(即n-(i-1)+1)可能是要找的数。
【例3】 有如下VB程序段:
i=1: j=6: s=””
Key=Val(Text1.Text)
Randomize
Do While i <=j
M=Int(Rnd*(j-i+1)+i)
If a(M)
ElseIf a(M)>Key Then
i=M+1
Else
Exit Do
End If
Loop
D
数组元素a(1)到a(6)的值依次为“88、72、53、29、24、12”,文本框Text1中输入的值是24,执行该程序段,下列查找顺序不可能出现的是( )
A.12 53 24 B.72 53 29 12 24
C.53 12 29 24 D.53 12 72 24
解析 表达式Int(Rnd*(j-i+1))的最大值为j-i,因此m的取值范围是[i,j]之间的一个数。对分查找是在一个区间[i,j]内进行查找中间位置m对应的数值a(m),若a(m)<>key,则j移动到前面区间[1,m-1]或i移动到[m+1,j]再次进行查找。A选项中,第2、3、4次查找的区间是依次是[1,5]、[4,5]、[5,5];B选项查找的区间依次是[1,6]、[3,6]、[4,6]、[4,5]、[5,5];C选项查找的区间依次是[1,6]、[4,6]、[4,5]、[5,5];D选项查找的区间依次是[1,6]、[4,6]、[4,5],而第3个数72不可能在区间[4,5]中。
【变式2】 已知直角三角形的斜边长度Key,利用对分查找算法计算其他两条整数边长的VB程序段如下:
flag=True : p=0
Key=5
For i=1 To Key-1
L=i
____①____
Do While____②____
M=(L+R)\2
p=p+1
If i*i+M*M
ElseIf i*i+M*M>Key*Key Then
R=M-1
Else
A
Text2.Text=Str(i)+” ”+Str(M)+” ”+Str(Key)
flag=False
i=Key
End If
Loop
Next i
If flag Then Text2.Text=”没有符合条件的整数勾股数对!”
上述程序段2个划线处的代码分别为( )
A.①R=Key-1 ②L<=R And flag
B.①R=Key ②L<=R And flag
C.①R=Key-1 ②L<=R Or flag
D.①R=Key-1 ②L<=R And flag=False
解析 L和R表示两条直角边长,R只能比斜边短。Flag表示是否找到的标志。
【变式3】 (2021·1月浙江选考)某对分查找算法的VB程序段如下:
′随机产生包含20个整型元素的升序序列,依次存入数组a,代码略
i=1:j=20:s=””
key=Val(Text1.Text)
Do While i<=j
m=(i+j)\2
s=s+Str(a(m))
If a(m)=key Then Exit Do ′Exit Do表示退出循环
If a(m)>key Then j=m-1 Else i=m+1
Loop
Text2.Text=s
C
在文本框Text1中输入待查找数,执行该程序段后,下列选项中,文本框Text2中显示的内容不可能的是( )
A.78 50 46 33 B.51 37 41 48
C.74 50 46 51 D.73 83 87 89
解析 考查了对分查找的识读。选项C:按照对分查找的特点,当找到50后,往左找到46,后面不会再找到大于50的数字,选项错误。
【变式4】 若数组元素a(1)到a(8)的值依次为“6,9,12,18,20,28,32,45”,查找key值的VB程序段:
i=1: j=8: c=0
Do While i <=j
Randomize
m=Int(Rnd*(j-i+1))+i
If Key=a(m) Then ExitDo
If a(m)>Key Then
j=m-1
c=c+1
Else
i=m+1
c=c-1
End If
Loop
A
若查找的key值为18,运行该段程序后,下列说法正确的是( )
A.c的值可能为0 B.j=m-1 至少要执行一次
C.程序结束时i>j D.i的值可能为5
解析 m是i到j之间的一个随机位置,当第一次产生m的值为4,找到要找到的数,此时c等于0,语句j=m-1可能没有被执行到。由于要查找的key值是存在的,产生的m小于4,将改为i为m+1,生产的m大于4,将改为j为m-1,即查找的区间左右边界不断地靠近4,即i不可能超过4,j的值不可能小于4,因此肯定在查找过程中退出循环,因此i<=j。
考点三 采用二叉树法模拟算法思想
在查找一个数的路径中,可以确定每次查找的数位置和值,可以判断查找次数,若找不到该数据时,可以判断此时变量i、j和m的值。大致可以分为以下几种情况:①随机给出查找值,求查找次数或查找路径;②给出查找次数或查找路径,求查找值的范围;③当查找成功时没有结束查找,求查找次数或查找的边界值。
【例4】 有如下VB程序段:
c=0: i=1: j=9
f=False
Key=Val(Text1.Text)
Do While i <=j And Not f
m=(i+j+1)\2
c=c+1
If Key=d(m) Then
f=True
ElseIf Key>d(m) Then
j=m-1
Else
i=m+1
End If
Loop
D
数据元素d(1)到d(9)的值依次为“98,85,71,54,37,30,24,15,9”,若运行该程序段后c的值为4,则Text1中输入的值不可能为( )
A.30或31 B.88或98 C.30或28 D.9或54
解析 由于要查找的key值未知,可以用二叉树法解题,但要注意m的计算方法。由图可知,能找到的情况是输入的第1或第6个数。找不到的情况是比第1个数大,或比第1个数但比第2个数大,或者比第5个数小,但比第6个数小,或者比第6个数大,但比第7个数小。
【例5】 某算法的VB程序段如下:
i=1: j=7: s=””
key=Int(Rnd*100)
Do While i <=j
m=(i+j)\2
If Key=a(m) Then
s=s+”M”: Exit Do
ElseIf Key
Else
i=m+1: s=s+”R”
End If
Loop
Text1.Text=s
C
数组元素a(1)到a(7)的值依次为“24,35,38,41,45,69,78”。执行该程序段后,文本框Text1中显示内容可能的是( )
A.RL B.LMR C.RLR D.LRLM
解析 第一次查找的位置是4,数值为41,此
时可能有三种处理结果,相等输出M,退出;
比41小,变量j左移,继续查找;比41大,变
量i右移,继续查找。以查找37、38和39为例,
先依次访问41和35,接着访问38,查找38的结
果是LRM,查找37的结果是LRL,查找39的结果是LRR。因此选项A只找到第二个结点,若找到了,则输出M,否则还可以向左或向右继续查找。选项B在找到情况下,不可能再次查找。选项C查找比第5个数大,但比第6个数小的数。选项D中LRL表示查找比第3个数大但比第4个数小的数,因此不可能再次找到。
【变式5】 对分查找程序如下:
i=1: j=15: n=0: Key=Val(Text1.Text)
Do While i <=j
m=(i+j)\2
If a(m)=Key Then
Exit Do
ElseIf a(m)>Key Then
j=m-1: n=n-1
Else
i=m+1: n=n+1
End If
Loop
B
执行该程序段后,n的值为-3,则下列说法正确的是( )
A.该程序若要实现对分查找,要求数组a按降序排列
B.查找key的值可能等于a(1)元素的值
C.查找key的值可能小于a(1)元素的值
D.查找key的值可能大于a(15)元素的值
解析 当条件a(m)>Key成立时,指针j=m-1,因此该数组是升序排列的。15个数,最多查找4次,n的值为-3,说明一直向左继续查找。找到结点8,4,2,1时的n值分别是0,-1,-2,-3,因此找到的数可能是a(1),若小于a(1)元素的值,n的值为-4,可能大于a(15)元素,n的值为4。
【变式6】 某算法程序段如下:
i=1: j=10: n=0
key=Int(Rnd*10)*2+1
Do While i <=j
m=Int((i+j)/2+0.5)
If key=a(m) Then
Exit Do
ElseIf key>a(m) Then
j=m-1: n=n-1
Else
i=m+1: n=n+1
End If
Loop
Text1.Text=Str(n)
A
已知数组元素 a(1)至 a(10)的值依次为 20,19,17,16,14,11,8,5,2,0若执行该程序后,文本框 Text1中显示的内容不可能是( )
A.-3 B.-2 C.-1 D.1
解析 key的值在1-19之间的奇数。采用二叉树法进行解题,当找到11时,n的值为0。当找到17时,n的值为-1,当找到19时,n的值为-2,19已经是要产生的key中最大值。若要查找的数7,则n的值为1。
C
【变式7】 某对分查找算法的 VB 程序段如下:
′数组元素f(1)到 f(9)赋初值为 0,代码略
Key=Val(Text1.Text):
i=1: j=9
Do While i <=j
m=(i+j)\2
f(m)=1
If a(m)=Key Then Exit Do ′Exit Do 表示退出循环
If a(m)>Key Then j=m-1 Else i=m+1
Loop
整型数组元素 a(1)到 a(9)为升序序列,在文本框 Text1 中输入待查找数,执行该程序段后,下列选项中,f(1)到 f(9)各元素值不可能的是( )
A.1,1,0,0,1,0,0,0,0 B.0,0,0,0,1,0,0,0,0
C.0,0,0,0,1,1,1,1,0 D.0,1,1,1,1,0,0,0,0
解析 本题对分查找算法。通过构建二叉树,
A选项访问的中间分别为 5、2、1,B选项若 key=a(5)时,查找一次,循环中途退出。D选项访问的中间分别为 5、2、3、4。
【例6】 (2020·5月柯桥)有如下VB程序段:
low=1: high=8
Key=Val(Text1.Text)
Do While low <=high
m=(low+high)\2
If a(m)>=Key Then
high=m-1
Else
low=m+1
End If
Loop
D
数组元素a(1)至a(8)中的分别为5,7,12,12,15,20,25,27,执行该程序段后,变量low的值为3,则文本框Text1中输入的值不可能是( )
A.10 B.11 C.12 D.13
解析 由于输入的值不知,因此可以采用二叉树来解决问题。当输入12时,找到了但未退出,而是向左查找,因此依次查找12、7和12,当找到12时,high=2,low=3,退出循环。输入10和11时,与访问12有路径是相同的。查找13时,依次查找12、20和15,low=5。
【变式8】 (2020·9月A9协作体)某对分查找算法的 VB程序段如下:
Key=Val(Text1.Text): s=””
i=1: j=10
Do While i <=j
m=(i+j)\2
If a(m)>Key Then
i=m+1
s=s+”R”
Else
j=m-1
s=s+”L”
End If
Loop
Text2.Text=s
B
数组元素a(1)到a(10)的值依次为“33,21,18,14,14,14,10,6,4,1”。在文本框Text1中输入14后,该程序段的输出结果与输入下列值的输出结果相同的是( )
A.10 B.16 C.19 D.3
解析 在查找过程中,若找到要找的数值key,没有结束查找,而是向左继续查找。画出二叉树,如图所示。最后一次查找第4个位置,且向左查找,因此只要查找的数介于第3和第4个之间的数,输出结果都是一样的。
【变式9】 (2020·9月之江教育)有如下VB程序段:
Dim a(1 To 8) As Integer
Dim i As Integer,j As Integer,m As Integer,k As Integer
i=1: j=8
a(1)=87: a(2)=66: a(3)=59: a(4)=40
a(5)=39: a(6)=30: a(7)=22: a(8)=13
k=Val(Text1.Text)
Do While i <=j
m=(j+i+1)\2
If a(m)
Text2.Text=Str(i)
A
程序执行完后,i的值是4,则k的值不可能是( )
A.40 B.41 C.48 D.59
解析 由于查找的值未知,因此往往采用二叉树法解题。
A选项找到第4个数40,还要向右查找,因此i的值为5。
B和C选项该数介于第3个和第4个数之间,找到第4个数后,改变j的值,向左查找。
D选项,当查找的k找到后,还要向右查找,此时i大于j。
【变式10】 下列VB程序段功能为:在升序排序数组a中(a(1)≤a(2)≤a(3)……)采用对分查找的方式查找某数值,若能找到,则输出该数值在数组a中的起始和结束位置,否则输出“找不到”。
Dim a(0 To 10) As Integer
Key=Val(Text1.Text)
i=1: j=10
Do While i <=j
m=(i+j)\2
If____①____ Then
j=m-1
E1se
i=m+1
End If
Loop
If a(j) <>Key Then
Label1.Caption=”找不到”
Else
p1=j
Do While Key=a(j) And j>=1
j=j-1
Loop
____②____
Label1.Caption=Str(p2)+”-”+Str(p1)
End If
程序划线处的代码应为( )
A.①keyC.①key<=a(m) ②p2=j D.①key<=a(n) ②p2=j+1
B
解析 从输出语句来看,p2和p1为该数值在数组a中的起始和结束位置,p1的初值为j,因此j是右极限位置,即当a(m)=key时,还要将i赋值为m+1,继续向右查找。从j的位置一直往前找,当条件Key=a(j)不成立时,j已经不再指向key了,最后一个等于key的位置是j+1。
【例7】 有如下VB程序段:
i=1: j=8: n=0: s=””
key=2
Do While i <=j
m=Int(Rnd*(j-i+1))+i
n=n+l: s=s+Str(m)
If a(m)=Key Then Label1.Caption=”找到第”+Str(m)+”个”
If Key>a(m) Then i=m+1 Else j=m-1
Loop
Label1.Caption=s
A
若数组a(1)~a(8)的值依次为“1,2,2,2,2,6,6,8”,程序段运行后,下列说法正确的是( )
A.m的值可能分别为3 2 1 B.m的值一定为2
C.找到第5个位置上的2 D.n的值可能为1
解析 m随机值在区间[i,j]内,由于循环中间没有执行退出,所以最后循环结束必然i大于j,并且i=j+1, 循环过程中key>a(m),向右缩减区间, key<=a(m),向左缩减区间,最后j一定会走到首个key位置的左边,此时i指向这个key,即第一个2,循环结束,最后i=2,j=1,而m取值可能为2,也可能是1。
1.某对分查找算法的VB程序段如下:
D
flag=False
i=0:j=6:c=0
Do While i <=j And flag=False
m=Fix((i+j)/2+0.5)
If Key=a(m) Then flag=True
If Key
Loop
数组元素a(0)到a(6)的值依次为“3,12,30,46,69,72,84”,Key的值为84。若该程序段执行后,以下说法中正确的是( )
A.i=6 B.j=7 C.m=7 D.c=3
解析 本题可以采用列表法解题,但要注意m的计算公式。当找到key时,并没有马上退出,而是执行了下一条IF语句,因此i的值为7。
i j m a(m)
0 6 3 46
4 6 5 72
6 6 6 84
2.数组a中依次存放6个有序数据“23 33 44 55 66 77”。
D
i=1: j=6: c=0: Key=35
Do While i <=j
c=c+1
m=(i+j)\2
If (j-i+1) Mod 2=0 Then m=m+1
If a(m)=Key Then Exit Do
If Key
该程序段运行后,下列各变量的值不正确的是( )
A.i=3 B.j=2 C.c=3 D.m=2
解析 本题可以采用列表法解题。
i j m a(m)
1 6 4 55
1 3 2 33
3 3 3 44
3 2
3.(2019·12月新力量联考)某对分查找算法的VB程序段如下:
Const n=100: Dim d(1 To 100) As Integer
For i=1 To 100
d(i)=i
Next i
Key=300
For i=1 To n-1
L=i+1: R=n
Do While L <=R
m=(L+R)\2
If d(i)*d(m)
ElseIf d(i)*d(m)>Key Then
R=m-1
Else
Label1.Caption=Str(d(i))+” ”+Str(d(m))
Exit Do
End If
Loop
Next i
If Label1.Caption=”” Then Label1.Caption=”没有符合的数对”
该程序段执行后,标签Label1中显示的内容是( )
A.3 100 B.15 20 C.50 6 D.没有符合的数对
解析 在[i+1,100]之间查找一个数,该数与i乘积等于300,注意两个要点,该数大于i且小于100。最小的数对为3和100,因此最大的数对为15和20,虽然50*6=300,但不符合大于i的条件。
B
4.(2019·12月稽阳)有如下 VB 程序:
a(1)=1
For i=2 To 12
a(i)=a(i-1)+Int(Rnd*2)+1
Next i
Key=Val(Text1.Text)
i=1: j=12: cnt=0: flag=False
Do While i <=j And flag=False
cnt=cnt+1
m=(i+j+1)\2
If a(m)=Key Then
flag=True
ElseIf Key>a(m) Then
i=m+1
Else
j=m-1
End If
Loop
程序运行后,下列说法正确的是( )
A.在Text1输入15,程序运行后m肯定为12
B.在Text1输入6,程序运行后cnt可能大于3
C.若查找不成功,则j>m肯定成立
D.若查找不成功,则i<=m肯定成立
B
解析 在第1个For语句中,可以得知,数组a中,从第2个数开始肯定比前面的数至少大1,因此a(12)的最小可能是12,最大可能是23。数15最大的位置可能在12,最小的位置可能是8,因此m的值在8~12均有可能。数6最大位置可能是6,最小位置可能是4,可以对左面半边进行分析,若查找的数在第4个位置,或者比第4个位置大,但比第5个位置小,均要查找3次。若查找不成功,j可能等于m-1,i有可能=m+1。
5.(2019·10月五校联考)某对分查找算法的 VB 程序段如下:
Key=Int(Rnd*49)*2+1
s=0: i=1: j=10
Do While i <=j
m=(i+j)\2
If Key=a(m) Then Exit Do
If Key
Else
i=m+1: s=2*s+1
End If
Loop
数组 a(1)到 a(10)的值依次为“2,6,7,15,20,24,27,43,52,63”,执行该程序段后,s 的值不可能为( )
A.2 B.3 C.5 D.15
解析 本题考核的是对分查找的算法。要查找的数在1至97之间的奇数。查找一次找到了,s等于0。第2次如果在左区间查找,s=0;在右区间查找并找到,s=1。第2次在右区间中查找不成功,继续向左查找,即找到第6个数,则s=2,但第6个数为偶数。向右查找,则s=3。可以使用二叉树法来解题。查找到第3个节点时,s=1,继续向左查找,s=2,该数范围在第2个节点和第3个节点之间,即[6,7]之间,该区间中没有整数,因此不可能。
A
6.某对分査找算法的VB程序段如下:
i=1: j=7: s=””:key=3
Do While i <=j
m=(i+j)\2
If key=a(m) Then s=s+”M”
If key
Else
i=m+1: s=s+”R”
End If
Loop
Text1.Text=s
C
数组元素a(1)到a(7)的值依次为“1,2,3,3,3,5,8”。若该程序段执行后,文本框Text1中显示的内容是( )
A.MRMR B.MLMR C.MRLMR D.LRLM
解析 查找过程中不断输出key与m位置的值进行比较,若相等则输出“M”但并没有结束查找,接着执行第二个选择结构,继续向右移动。访问中点m的值依次为4,6,5,此时i和j的值均等于5,i继续向右移动,条件i<=j不成立,退出循环。在结点4和5分别输出两个字母,且都为MR,因此文本框中输出MRLMR。
C
7.某算法的VB程序段如下:
key=Int(Rnd*5)*2+11
i=1:j=8:c=0
Do While i<=j
m=(i+j+1)\2
If a(m)>=key Then i=m+1 Else j=m-1
c=c+1
Loop
数组元素a(1)到a(8)的值依次为“23,21,19,18,16,15,14,11”。 若该程序段执行后,下列说法错误的是( )
A.i的值为j+1 B.i的值可能是9
C.j的值可能是5 D.c的值一定是3
解析 产生key值的范围是11至19之间的奇数,
即只能产生在第3个到第8个之间的数。程序代
码中,找到key时,并没有退出查找,而是向右
继续查找,因此退出循环时,肯定满足条件i>j,
即i=j+1。画出二叉树如图所示。若i要达到最大值,则必须一直向右查找,当要找的数是11时,i达到极值9,此时j=m=8,查找结束。从图中可知,当找到a(5),a(3),a(7)时并没有结束查找,因此必须要查找3次才能退出。j的值若要为5,则查找的数比a(5)小但比a(6)大,但a(5)和a(6)之间没有相应的奇数。
8.某对分查找算法的 VB 程序段如下:
n=0: i=l: j=8
Key=Val(Text1.Text)
Do While i <=j
m=(i+j)\2
n=n+1
If Key=d(m) Then Exit Do
If Key>d(m) Then j=m-1 Else i=m+1
Loop
If i <=j Then s=Str(m-n) Else s=Str(n)
B
数组元素d(1)到d(8)的值依次为“87,75,50,44,36,24,15,8”,输入某个key值,运行该程序段后,变量s结果为2,则输入key的值是( )
A.75 B.36 C.24 D.15
解析 由于输入key未知,可以采用二叉树法。变量n表示查找次数,m表示找到值的结点。若找到该数,s的值为m-n,若没有找到值为n。查找2次,显然不可能是没有找到。输入key的值为36,m的值为5,找了3次。
同课章节目录
