七年级数学下册期末总复习课件:第七章 三角形
文档属性
| 名称 | 七年级数学下册期末总复习课件:第七章 三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 676.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-04 16:56:32 | ||
图片预览








文档简介
(共27张PPT)
三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(1)边:
组成三角形的三条线段叫做三角形的边.
(2)顶点:
点A,B,C是三角形的顶点.
(3)角:
相邻的两边组成的角,叫三角形的内角,简称三角形的角.
C
A
B
a
c
b
三角形的表示方法
(1)顶点为A,B,C的三角形,记作“△ABC”,读作“三角形ABC”.
(2)三角形的三边既可以用两个大写字母表示,也可以用一个小写字母表示.当用小写字母表示时,顶点所对的边就用该顶点的小写字母表示.例如顶点A所对的边可以用a表示.
C
A
B
a
c
b
练一练
如图,图中共有几个三角形?分别是哪些?
答:10个.分别是
△ABD,△ABE,△ABF ,△ABC ,△ADE ,△ADF ,△ADC ,△AEF ,△AEC ,△AFC
三角形的分类
三角形有两种分类方法:
三角形的三边关系
(1)三角形两边之和大于第三边.
(2)三角形两边之差小于第三边.
练一练
C
19cm或17cm
2
练一练
1.等腰三角形的底边BC=8 cm,且|AC-BC|=2 cm,则腰长AC为( )
A.10 cm或6 cm B.10 cm
C.6 cm D.8 cm或6 cm
A
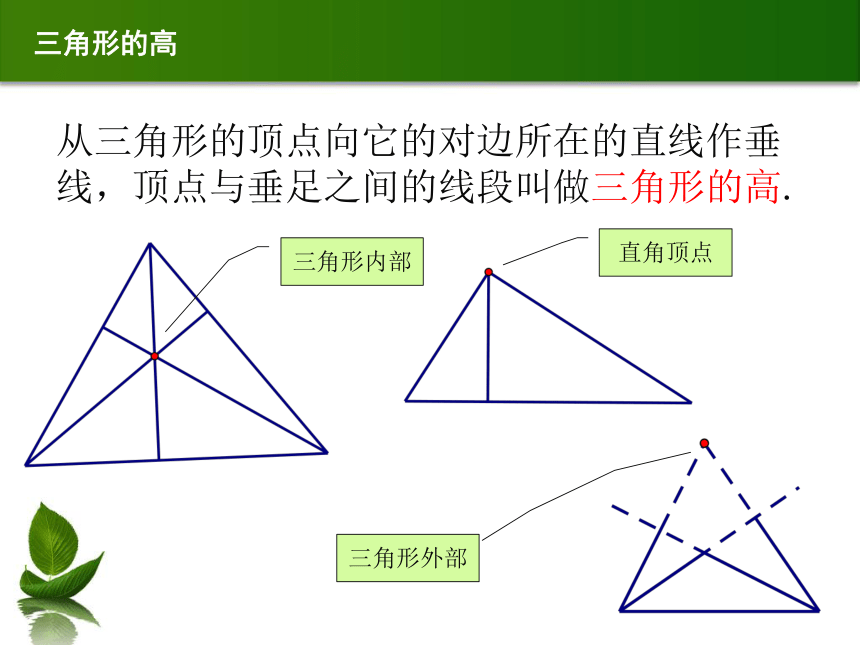
三角形的高
从三角形的顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高.
三角形内部
直角顶点
三角形外部
练一练
如图所示:△ABC中,AD⊥BC于D, BE⊥AC于E, CF⊥AB于F,则△OBC的高是______.OF是_________________________的高?
OD
△OAB, △OFB, △OAF
三角形的中线
连接三角形的一个顶点和它对边中点的线段,叫做三角形的中线.
三角形的一条中线将三角形分成面积相等的两部分.
三角形内部
如图所示:△ABC中,D,E分别为BC,AD的中点,且S △ABC=4,则S阴为_____.
1
三角形的角平分线
作三角形一个内角的角平分线,与这个角的对边有一个交点,交点与顶点之间的线段叫做三角形的角平分线.
三角形内部一点
三角形的稳定性
三角形具有稳定性.
三角形的内角和
三角形三个内角的和等于180゜.
练一练
1.如图,则△ABC的形状是( ) A、锐角三角形
B、钝角三角形
C、直角三角形
D、等腰三角形
2.如图, ∠A+∠B+∠C+∠D
+∠E+∠F=________.
C
360°
练一练
直角
30°
60°
90°
80°
60°
40°
70°
60°
50°
三角形的外角
1.三角形的一边与另一边的延长线组成的角叫做三角形的外角.
2.三角形的外角和
三角形的外角和等于360゜.
3.三角形的外角相关定理:
(1)三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的一个外角大于与它不相邻的任何一个内角.
练一练
1.下列能说明∠1>∠2的是( )
C
2.如图所示,在△ABC中,下列说法正确的是( ).
A.∠ADB>∠ADE; B.∠ADB>∠1+∠2+∠3;
C.∠ADB>∠1+∠2;
D.以上都对.
C
练一练
1.在三角形中,已知外角是相邻的内角的2倍,则它的外角为_______,内角为_________
2.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为_____________.
3.一个三角形的三个外角中,最多有_____个角是锐角.
4.如果一个三角形的各内角与一个外角的
和是225°,则与这个外角相邻的内角是__________度.
120°
60°
3:2:1
1
135
练一练
1.AB∥CD, ∠A=45°∠C=80°,求∠M的度数.
2.如图,直线DE与△ABC的三边所在直线交与点D、E、F, ∠ A=40°, ∠ D=25°,DE⊥AB,求∠ ACB的度数.
35°
75°
练一练
在△ABC中,求证:∠D>∠A.
练一练
如图,AB∥CD,EF与AB、CD分别相交于点E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且∠ BEP=40°,求∠EPF的度数.
65゜
练一练
一个零件的形状如图所示,按规定∠A=100°,AB与CD,AF与DE的夹角分别为32°和22°,检查员量得∠CDE=150°,这个零件合格吗?请说明理由.
不合格。
练一练
如图,从A处观测C处仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C外观测A、B两处时视角∠ACB是多少度?
15°
练一练
如图,∠1=∠2=30°,∠3=∠4,∠A=80,则x= ,y=________.
130°
50°
长风破浪会有时
直挂云帆济沧海
三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(1)边:
组成三角形的三条线段叫做三角形的边.
(2)顶点:
点A,B,C是三角形的顶点.
(3)角:
相邻的两边组成的角,叫三角形的内角,简称三角形的角.
C
A
B
a
c
b
三角形的表示方法
(1)顶点为A,B,C的三角形,记作“△ABC”,读作“三角形ABC”.
(2)三角形的三边既可以用两个大写字母表示,也可以用一个小写字母表示.当用小写字母表示时,顶点所对的边就用该顶点的小写字母表示.例如顶点A所对的边可以用a表示.
C
A
B
a
c
b
练一练
如图,图中共有几个三角形?分别是哪些?
答:10个.分别是
△ABD,△ABE,△ABF ,△ABC ,△ADE ,△ADF ,△ADC ,△AEF ,△AEC ,△AFC
三角形的分类
三角形有两种分类方法:
三角形的三边关系
(1)三角形两边之和大于第三边.
(2)三角形两边之差小于第三边.
练一练
C
19cm或17cm
2
练一练
1.等腰三角形的底边BC=8 cm,且|AC-BC|=2 cm,则腰长AC为( )
A.10 cm或6 cm B.10 cm
C.6 cm D.8 cm或6 cm
A
三角形的高
从三角形的顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高.
三角形内部
直角顶点
三角形外部
练一练
如图所示:△ABC中,AD⊥BC于D, BE⊥AC于E, CF⊥AB于F,则△OBC的高是______.OF是_________________________的高?
OD
△OAB, △OFB, △OAF
三角形的中线
连接三角形的一个顶点和它对边中点的线段,叫做三角形的中线.
三角形的一条中线将三角形分成面积相等的两部分.
三角形内部
如图所示:△ABC中,D,E分别为BC,AD的中点,且S △ABC=4,则S阴为_____.
1
三角形的角平分线
作三角形一个内角的角平分线,与这个角的对边有一个交点,交点与顶点之间的线段叫做三角形的角平分线.
三角形内部一点
三角形的稳定性
三角形具有稳定性.
三角形的内角和
三角形三个内角的和等于180゜.
练一练
1.如图,则△ABC的形状是( ) A、锐角三角形
B、钝角三角形
C、直角三角形
D、等腰三角形
2.如图, ∠A+∠B+∠C+∠D
+∠E+∠F=________.
C
360°
练一练
直角
30°
60°
90°
80°
60°
40°
70°
60°
50°
三角形的外角
1.三角形的一边与另一边的延长线组成的角叫做三角形的外角.
2.三角形的外角和
三角形的外角和等于360゜.
3.三角形的外角相关定理:
(1)三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的一个外角大于与它不相邻的任何一个内角.
练一练
1.下列能说明∠1>∠2的是( )
C
2.如图所示,在△ABC中,下列说法正确的是( ).
A.∠ADB>∠ADE; B.∠ADB>∠1+∠2+∠3;
C.∠ADB>∠1+∠2;
D.以上都对.
C
练一练
1.在三角形中,已知外角是相邻的内角的2倍,则它的外角为_______,内角为_________
2.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为_____________.
3.一个三角形的三个外角中,最多有_____个角是锐角.
4.如果一个三角形的各内角与一个外角的
和是225°,则与这个外角相邻的内角是__________度.
120°
60°
3:2:1
1
135
练一练
1.AB∥CD, ∠A=45°∠C=80°,求∠M的度数.
2.如图,直线DE与△ABC的三边所在直线交与点D、E、F, ∠ A=40°, ∠ D=25°,DE⊥AB,求∠ ACB的度数.
35°
75°
练一练
在△ABC中,求证:∠D>∠A.
练一练
如图,AB∥CD,EF与AB、CD分别相交于点E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且∠ BEP=40°,求∠EPF的度数.
65゜
练一练
一个零件的形状如图所示,按规定∠A=100°,AB与CD,AF与DE的夹角分别为32°和22°,检查员量得∠CDE=150°,这个零件合格吗?请说明理由.
不合格。
练一练
如图,从A处观测C处仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C外观测A、B两处时视角∠ACB是多少度?
15°
练一练
如图,∠1=∠2=30°,∠3=∠4,∠A=80,则x= ,y=________.
130°
50°
长风破浪会有时
直挂云帆济沧海
