作轴对称图形
图片预览







文档简介
(共30张PPT)
活动1
观察图片
操作:自己动手在纸上画一个图案,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置再试一次,你又得到了什么?
想一想
观察你画的图形:
新图形和原图形有什么关系?
成轴对称
对称轴是:
折痕所在的 直线,既直线l
图中的直线l 与PP’有什么关系?
我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案
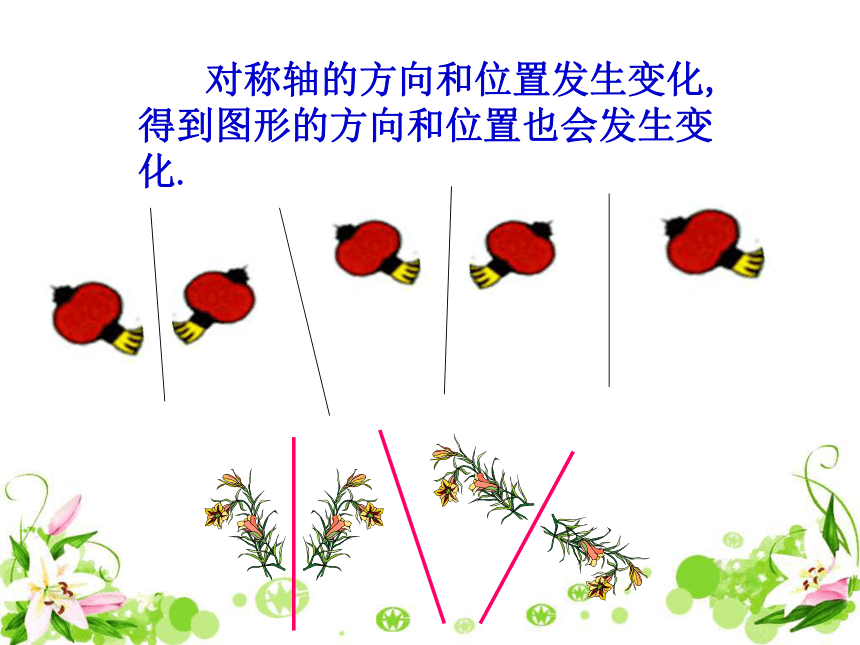
对称轴的方向和位置发生变化,得到图形的方向和位置也会发生变化.
由一个平面图形可以得到它关于一条直线l成轴对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
连接任意一 对对应点的线段被对称轴垂直平分。
归纳:
如果有一 个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?
思考
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
O
l
作法:
过点A作直线l的垂线在垂线上截取OA’=OA,垂足为点O,点A’就是点A关于直线l的对称点.
探究一
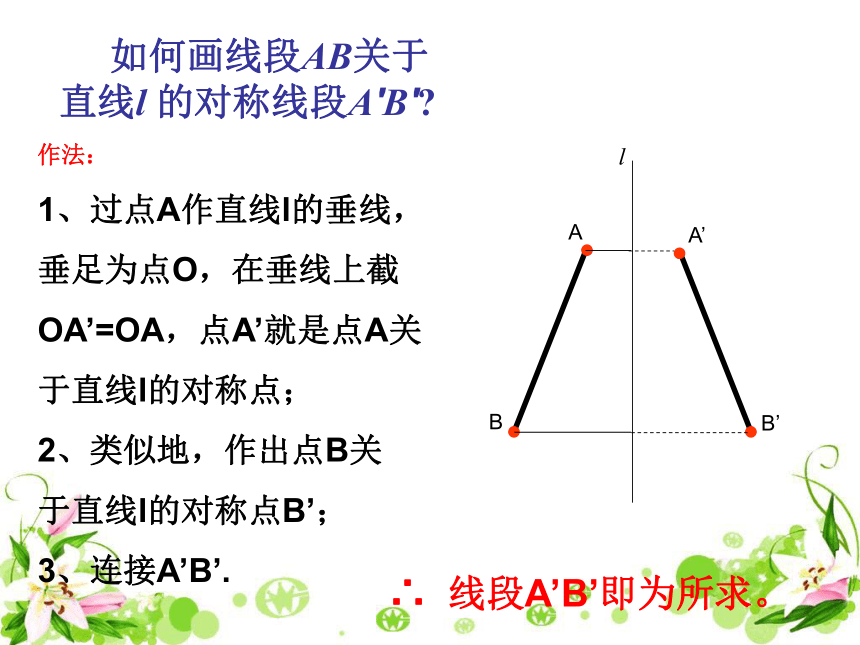
如何画线段AB关于
直线l 的对称线段A′B′
A
B
A’
B’
作法:
1、过点A作直线l的垂线,
垂足为点O,在垂线上截
OA’=OA,点A’就是点A关
于直线l的对称点;
2、类似地,作出点B关
于直线l的对称点B’;
3、连接A’B’.
∴ 线段A’B’即为所求。
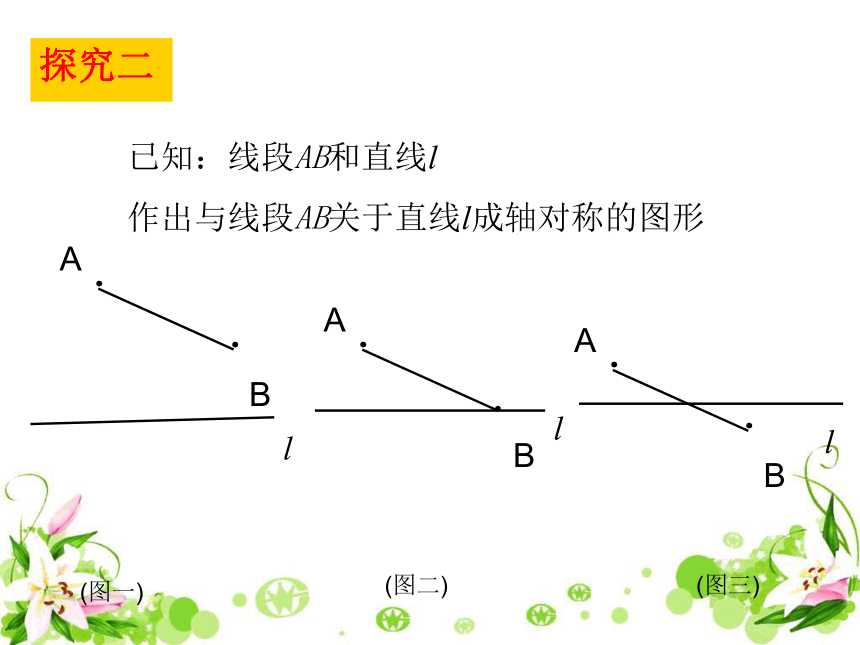
探究二
已知:线段AB和直线l
作出与线段AB关于直线l成轴对称的图形
A
B
﹒
﹒
l
l
l
A
B
﹒
﹒
A
B
﹒
·
(图一)
(图二)
(图三)
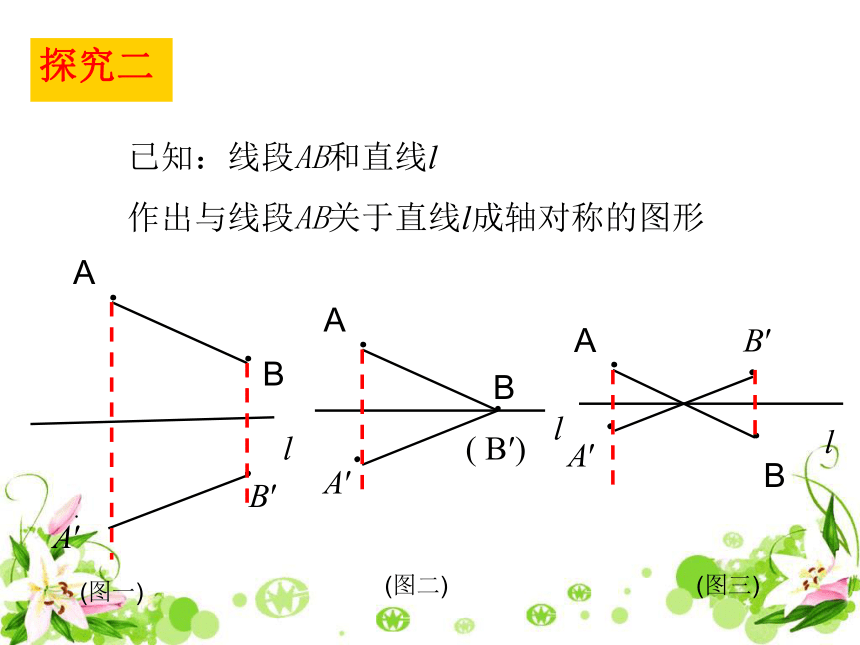
探究二
已知:线段AB和直线l
作出与线段AB关于直线l成轴对称的图形
A
B
﹒
﹒
l
l
l
A
B
﹒
﹒
A
B
﹒
·
(图一)
(图二)
(图三)
﹒
﹒
﹒
﹒
﹒
A′
B′
B′
( B′)
A′
A′
1、过点A作直线l的垂线,垂足为点O,
在垂线上截取OA’=OA,
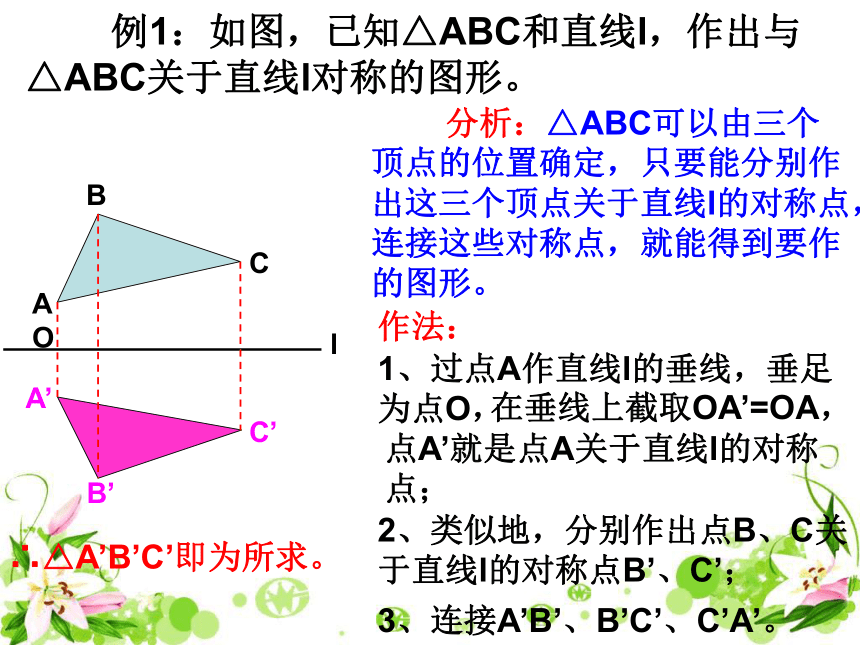
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求。
A’
B’
C’
O
点A’就是点A关于直线l的对称点;
我行了:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
B
A
C
l
B’
C’
B
A
C
A’
B’
∴△AB’C’即为所求。
作法:
1、分别作出点B、C关于直线l的对称点B’、C’;
2、连接AB’、B’C’、C’A。
B
A
C
l
作法:
1、分别作出点A、B关于直线l的对称点A’、B’;
2、连接A’B’、B’C、CA’。
∴△A’B’C即为所求。
归纳:
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形;
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接对称点,就可以得到原图形的轴对称图形。
利用轴对称,可以设计出精美的图案。请你用所学的知识来欣赏下列美丽的图案
花边艺术
中外建筑
景东文庙
景东文庙
景东文庙
云南景东县文庙
始建于清康熙二十一年(公元1682年),至今已有323年的历史
法国埃菲尔铁塔
雕刻家 威廉斯·多佛
《木制卫兵雕像》
1971
下面的第二个时间可由第一个怎样变换而得到
如果有一个图形和一条直线,作出与这个图形关于这条直线对称的图形,你会了吗
我来试一试,
第41页练习1
我们一起来 吧!
2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合.
练习
1.如图,把下列图形补成关于直线l对称的图形。
通过今天的学习,
你有什么收获与体会?
作业
由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点,都是原图形上的某一点关于直线L的对称点;
连接任意一 对对应点的线段被对称轴垂直平分。
归纳1:
归纳2:
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形;
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接对称点,就可以得到原图形的轴对称图形。
即概括为:1、找点 (确定图形中的一些特殊点);
3、连线(连接对称点)。
2、画点(画出特殊点关于已知直线的对称点);
习题19.2 第 1、5题
作业:P18
活动1
观察图片
操作:自己动手在纸上画一个图案,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置再试一次,你又得到了什么?
想一想
观察你画的图形:
新图形和原图形有什么关系?
成轴对称
对称轴是:
折痕所在的 直线,既直线l
图中的直线l 与PP’有什么关系?
我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案
对称轴的方向和位置发生变化,得到图形的方向和位置也会发生变化.
由一个平面图形可以得到它关于一条直线l成轴对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
连接任意一 对对应点的线段被对称轴垂直平分。
归纳:
如果有一 个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?
思考
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
O
l
作法:
过点A作直线l的垂线在垂线上截取OA’=OA,垂足为点O,点A’就是点A关于直线l的对称点.
探究一
如何画线段AB关于
直线l 的对称线段A′B′
A
B
A’
B’
作法:
1、过点A作直线l的垂线,
垂足为点O,在垂线上截
OA’=OA,点A’就是点A关
于直线l的对称点;
2、类似地,作出点B关
于直线l的对称点B’;
3、连接A’B’.
∴ 线段A’B’即为所求。
探究二
已知:线段AB和直线l
作出与线段AB关于直线l成轴对称的图形
A
B
﹒
﹒
l
l
l
A
B
﹒
﹒
A
B
﹒
·
(图一)
(图二)
(图三)
探究二
已知:线段AB和直线l
作出与线段AB关于直线l成轴对称的图形
A
B
﹒
﹒
l
l
l
A
B
﹒
﹒
A
B
﹒
·
(图一)
(图二)
(图三)
﹒
﹒
﹒
﹒
﹒
A′
B′
B′
( B′)
A′
A′
1、过点A作直线l的垂线,垂足为点O,
在垂线上截取OA’=OA,
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求。
A’
B’
C’
O
点A’就是点A关于直线l的对称点;
我行了:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
B
A
C
l
B’
C’
B
A
C
A’
B’
∴△AB’C’即为所求。
作法:
1、分别作出点B、C关于直线l的对称点B’、C’;
2、连接AB’、B’C’、C’A。
B
A
C
l
作法:
1、分别作出点A、B关于直线l的对称点A’、B’;
2、连接A’B’、B’C、CA’。
∴△A’B’C即为所求。
归纳:
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形;
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接对称点,就可以得到原图形的轴对称图形。
利用轴对称,可以设计出精美的图案。请你用所学的知识来欣赏下列美丽的图案
花边艺术
中外建筑
景东文庙
景东文庙
景东文庙
云南景东县文庙
始建于清康熙二十一年(公元1682年),至今已有323年的历史
法国埃菲尔铁塔
雕刻家 威廉斯·多佛
《木制卫兵雕像》
1971
下面的第二个时间可由第一个怎样变换而得到
如果有一个图形和一条直线,作出与这个图形关于这条直线对称的图形,你会了吗
我来试一试,
第41页练习1
我们一起来 吧!
2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合.
练习
1.如图,把下列图形补成关于直线l对称的图形。
通过今天的学习,
你有什么收获与体会?
作业
由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点,都是原图形上的某一点关于直线L的对称点;
连接任意一 对对应点的线段被对称轴垂直平分。
归纳1:
归纳2:
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形;
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接对称点,就可以得到原图形的轴对称图形。
即概括为:1、找点 (确定图形中的一些特殊点);
3、连线(连接对称点)。
2、画点(画出特殊点关于已知直线的对称点);
习题19.2 第 1、5题
作业:P18
