2021-2022学年数学人教A版(2019)选择性必修第一册3.3.2 抛物线的简单几何性质 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册3.3.2 抛物线的简单几何性质 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 11:03:22 | ||
图片预览






文档简介
(共23张PPT)
3.3.2
抛物线的简单几何性质
高二数学选择性必修第一册 第三章 圆锥曲线的方程
学习目标
1.掌握抛物线的的简单几何性质;
2.能用抛物线的的简单几何性质解决一些简单的问题;
3.理解数形结合的思想.
4.核心素养:数学运算、数学建模.
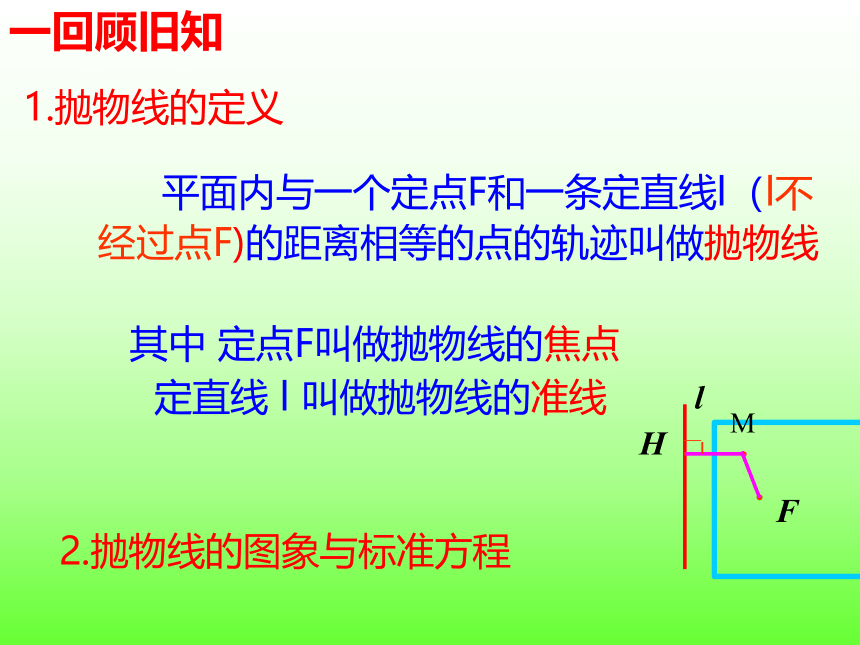
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
l
H
F
M
·
·
一回顾旧知
1.抛物线的定义
2.抛物线的图象与标准方程
图 象 方 程 焦 点 准 线
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
二、探究新知
1.范围
关于x轴
对称
即点(x,-y) 也在抛物线上,
故抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
定义:抛物线与它的轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令y=0,则x=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
3.顶点
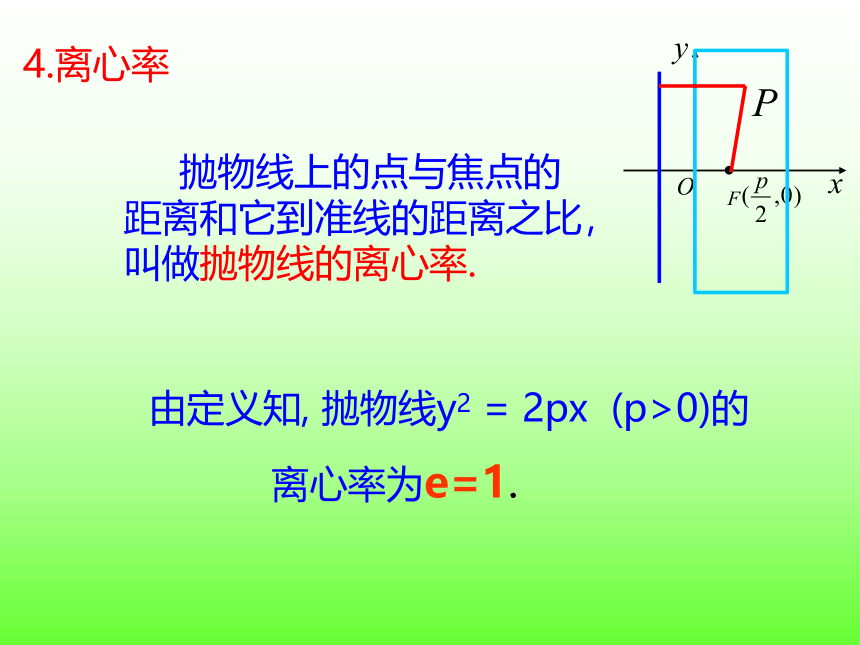
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的
离心率为e=1.
4.离心率
x
y
O
F
A
B
y2=2px
2p
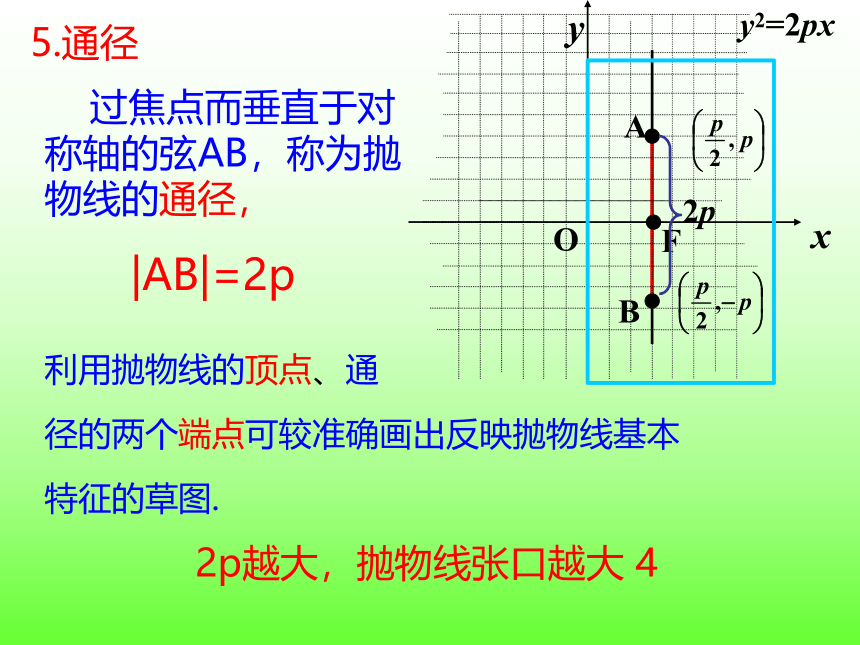
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通
|AB|=2p
2p越大,抛物线张口越大 4
5.通径
径的两个端点可较准确画出反映抛物线基本
特征的草图.
连接抛物线任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
x
y
O
F
P
6.焦半径
方程
图
形
范围
对称性
顶点
焦半径
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
(1)抛物线只位于半个坐标平面内,虽然它也可以
无限延伸,但没有渐近线;
(2)抛物线只有一条对称轴,没有对称中心;
(3)抛物线只有一个顶点,一个焦点,一条准线;
(4)抛物线的离心率e是确定的为1,
⑸抛物线的通径为2P, 2p越大,抛物线的张口越大.
归纳:
解:
设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
三、巩固新知
1.例3.已知抛物线关于x轴对称,它的顶点在坐标
原点,并且经过点M(2, )求它的标准方程.
由题意
2.变式
求适合下列条件的抛物线的标准方程
1).关于x轴对称,并且经过点M(5,-4);
2).关于y轴对称,准线经过点E(5,-5);
3).准线在y轴的右侧,顶点到准线的距离是4;
4).焦点在y轴的负半轴上,经过横坐标为16的点P,
且FP平行于准线.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
已知抛物线 截直线y=x+b所得弦长为4,
求b的值.
4.变式
解:
5.例5.
y
O
A
B
D
F
x
证明:
建立如图所示的坐标系设抛物线的
6.例6.
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
四、课堂小结
作业: 课本P138 习题3.3 10、11题
3.3.2
抛物线的简单几何性质
高二数学选择性必修第一册 第三章 圆锥曲线的方程
学习目标
1.掌握抛物线的的简单几何性质;
2.能用抛物线的的简单几何性质解决一些简单的问题;
3.理解数形结合的思想.
4.核心素养:数学运算、数学建模.
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
l
H
F
M
·
·
一回顾旧知
1.抛物线的定义
2.抛物线的图象与标准方程
图 象 方 程 焦 点 准 线
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
二、探究新知
1.范围
关于x轴
对称
即点(x,-y) 也在抛物线上,
故抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
定义:抛物线与它的轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令y=0,则x=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
3.顶点
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的
离心率为e=1.
4.离心率
x
y
O
F
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通
|AB|=2p
2p越大,抛物线张口越大 4
5.通径
径的两个端点可较准确画出反映抛物线基本
特征的草图.
连接抛物线任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
x
y
O
F
P
6.焦半径
方程
图
形
范围
对称性
顶点
焦半径
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
(1)抛物线只位于半个坐标平面内,虽然它也可以
无限延伸,但没有渐近线;
(2)抛物线只有一条对称轴,没有对称中心;
(3)抛物线只有一个顶点,一个焦点,一条准线;
(4)抛物线的离心率e是确定的为1,
⑸抛物线的通径为2P, 2p越大,抛物线的张口越大.
归纳:
解:
设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
三、巩固新知
1.例3.已知抛物线关于x轴对称,它的顶点在坐标
原点,并且经过点M(2, )求它的标准方程.
由题意
2.变式
求适合下列条件的抛物线的标准方程
1).关于x轴对称,并且经过点M(5,-4);
2).关于y轴对称,准线经过点E(5,-5);
3).准线在y轴的右侧,顶点到准线的距离是4;
4).焦点在y轴的负半轴上,经过横坐标为16的点P,
且FP平行于准线.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
3.例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
已知抛物线 截直线y=x+b所得弦长为4,
求b的值.
4.变式
解:
5.例5.
y
O
A
B
D
F
x
证明:
建立如图所示的坐标系设抛物线的
6.例6.
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
四、课堂小结
作业: 课本P138 习题3.3 10、11题
