安徽省合肥瑶海区三十中2021-2022学年九年级上期中模拟数学试卷(WORD版,含答案)
文档属性
| 名称 | 安徽省合肥瑶海区三十中2021-2022学年九年级上期中模拟数学试卷(WORD版,含答案) | 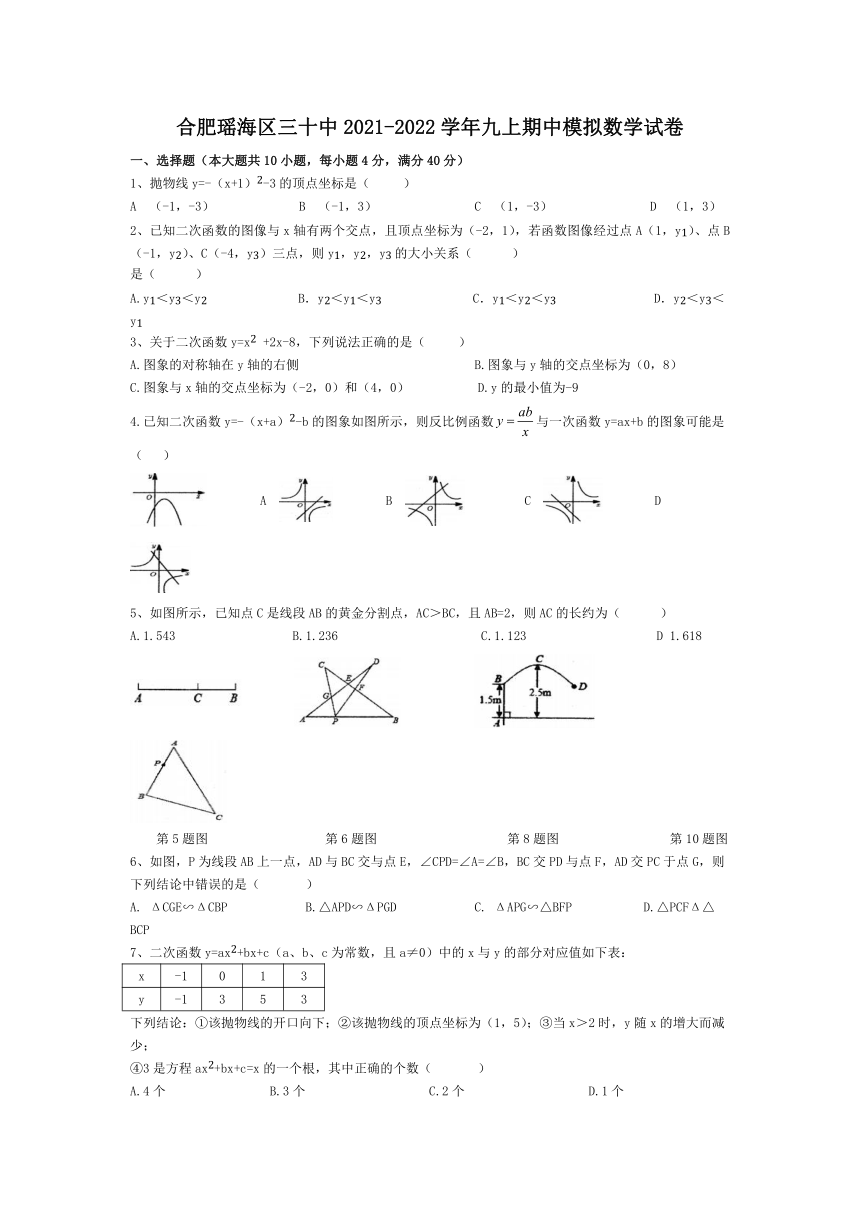 | |
| 格式 | zip | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 11:24:46 | ||
图片预览



文档简介
合肥瑶海区三十中2021-2022学年九上期中模拟数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=-(x+1)2-3的顶点坐标是( )
A (-1,-3) B (-1,3) C (1,-3) D (1,3)
2、已知二次函数的图像与x轴有两个交点,且顶点坐标为(-2,1),若函数图像经过点A(1,y1)、点B(-1,y2)、C(-4,y3)三点,则y1,y2,y3的大小关系( )
是( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
3、关于二次函数y=x2 +2x-8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧 B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(-2,0)和(4,0) D.y的最小值为-9
4.已知二次函数y=-(x+a)2-b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A B C D
5、如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D 1.618
第5题图 第6题图 第8题图 第10题图
6、如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A. ΔCGE∽ΔCBP B.△APD∽ΔPGD C. ΔAPG∽△BFP D.△PCFΔ△BCP
7、二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
x -1 0 1 3
y -1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;
④3是方程ax2+bx+c=x的一个根,其中正确的个数( )
A.4个 B.3个 C.2个 D.1个
8、如图是一款抛物线型落地灯简示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
9、如图,在矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向终点B以2cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1cm/s的速度运动至点D停止,如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2), 则y与x之间的函数关系用图象表示大致是( )
A B C D
10、如图,点Р是等腰△ABC的腰AB上的一点,过点Р作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
二、填空题(本大题共4小题,每小题5分,满分20分)
11、对于二次函数y=x2-4x+3,图象的对称轴为 ,当自变量x满足a≤x≤3时,函数值y的取值范围为-1≤y≤0,则a的取值范围为 .
12、已知反比例函数,若x≥2,则y的取值范围为 .
13、如图,在△ABC中,点E在BC上,且BE=3EC,D是AC的中点,AE、BD交于点F,
则的值为 .
14、如果一个正比例函数的图象与反比例函数的图象交于A(x1,y1),B(x2,y2)两点,那么(x2-x1)(y2-y1)的值为 ·
三、(本大题共2小题,每小题8分,满分16分)
15、已知:二次函数y= x2 -4x +3a+2 (a为常数).
(1)请写出该二次函数图像的对称轴; (2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图像在x≤4的部分与一次函数y =2x-1的图像有两个交点,求a的取值范围.
16、如图,在平面直角坐标系xOy中,直线y=-2x-3与双曲线交于M(a,2),N(1,b)两点。
(1)求k、a、b的值; (2)若Р是y轴上一点,且△MPN的面积是7,直接写出点P的坐标;
四、(本大题共2小题,每小题8分,满分16分)
17、已知xyz≠0 且=k,求k的值.
18、如图:AD∥EG∥BC,EG分别交AB、DB、AC于点E、F、G,已知AD=5,BC=10,AE=9,AB=12.求EG、FG的长.
五、(本大题共2小题,每小题10分,满分20分)
19、新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包。经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包,其销售单价不低于进价,销售利润率不高于180%。设每包销售价为x元(x为正整数)
(1)请直接写出的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
20、如图,点M是AB上一点,AE与BD交于点C,∠DME =∠A =∠B = a,且DM交AC于F,ME交BC于G
(1)求证:△AMF∽△BGM; (2)请你再写出两对相似三角形.
六、(本题满分12分)
21、已知抛物线y = mx2 + 2mx + 3m2 - 4
(1)该抛物线的对称轴为 ;
(2)若该抛物线的顶点在x轴上,求抛物线的函数表达式;
(3)设点M(n,y1)、N(2,y2)在该抛物线上,若y1>y2,求n的取值范围.
七、(本题满分12分)
22、如图,直线y=2x+6与反比例函数(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线
y =n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM。
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6->0的解集;
(3)直线y =n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
八、(本题满分14分)
23、某服装批发市场销售一种衬衫,衬衫每件进价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫中获得24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫每件的利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值?最大利润是多少?
合肥瑶海区三十中2021-2022学年九上期中模拟数学试卷答案
1 2 3 4 5 6 7 8 9 10
A A D D B A B A A B
11、 直线x=2; 1<a≤2; 12、 0<y≤3; 13、 ; 14、 -16;
15、 (1) 直线x=2; (2)a=3; (3)≤a<2;
16、(1)a=-2.5、 b=-5、 k=-5; (2)(0,1)或(0,-7)
17、 当x+y+z≠0时,k=2或当x+y+z=0,即x+y=-z,k=-1;
18、EG=; FG=;
19、(1)10≤x≤28; (2)定价每包28元,最大利润15840元;
(1)y=-20x+2600; (2)定价为70元; (3)x=75时,w取最大值为27500元;
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=-(x+1)2-3的顶点坐标是( )
A (-1,-3) B (-1,3) C (1,-3) D (1,3)
2、已知二次函数的图像与x轴有两个交点,且顶点坐标为(-2,1),若函数图像经过点A(1,y1)、点B(-1,y2)、C(-4,y3)三点,则y1,y2,y3的大小关系( )
是( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
3、关于二次函数y=x2 +2x-8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧 B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(-2,0)和(4,0) D.y的最小值为-9
4.已知二次函数y=-(x+a)2-b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A B C D
5、如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D 1.618
第5题图 第6题图 第8题图 第10题图
6、如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A. ΔCGE∽ΔCBP B.△APD∽ΔPGD C. ΔAPG∽△BFP D.△PCFΔ△BCP
7、二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
x -1 0 1 3
y -1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;
④3是方程ax2+bx+c=x的一个根,其中正确的个数( )
A.4个 B.3个 C.2个 D.1个
8、如图是一款抛物线型落地灯简示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
9、如图,在矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向终点B以2cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1cm/s的速度运动至点D停止,如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2), 则y与x之间的函数关系用图象表示大致是( )
A B C D
10、如图,点Р是等腰△ABC的腰AB上的一点,过点Р作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
二、填空题(本大题共4小题,每小题5分,满分20分)
11、对于二次函数y=x2-4x+3,图象的对称轴为 ,当自变量x满足a≤x≤3时,函数值y的取值范围为-1≤y≤0,则a的取值范围为 .
12、已知反比例函数,若x≥2,则y的取值范围为 .
13、如图,在△ABC中,点E在BC上,且BE=3EC,D是AC的中点,AE、BD交于点F,
则的值为 .
14、如果一个正比例函数的图象与反比例函数的图象交于A(x1,y1),B(x2,y2)两点,那么(x2-x1)(y2-y1)的值为 ·
三、(本大题共2小题,每小题8分,满分16分)
15、已知:二次函数y= x2 -4x +3a+2 (a为常数).
(1)请写出该二次函数图像的对称轴; (2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图像在x≤4的部分与一次函数y =2x-1的图像有两个交点,求a的取值范围.
16、如图,在平面直角坐标系xOy中,直线y=-2x-3与双曲线交于M(a,2),N(1,b)两点。
(1)求k、a、b的值; (2)若Р是y轴上一点,且△MPN的面积是7,直接写出点P的坐标;
四、(本大题共2小题,每小题8分,满分16分)
17、已知xyz≠0 且=k,求k的值.
18、如图:AD∥EG∥BC,EG分别交AB、DB、AC于点E、F、G,已知AD=5,BC=10,AE=9,AB=12.求EG、FG的长.
五、(本大题共2小题,每小题10分,满分20分)
19、新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包。经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包,其销售单价不低于进价,销售利润率不高于180%。设每包销售价为x元(x为正整数)
(1)请直接写出的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
20、如图,点M是AB上一点,AE与BD交于点C,∠DME =∠A =∠B = a,且DM交AC于F,ME交BC于G
(1)求证:△AMF∽△BGM; (2)请你再写出两对相似三角形.
六、(本题满分12分)
21、已知抛物线y = mx2 + 2mx + 3m2 - 4
(1)该抛物线的对称轴为 ;
(2)若该抛物线的顶点在x轴上,求抛物线的函数表达式;
(3)设点M(n,y1)、N(2,y2)在该抛物线上,若y1>y2,求n的取值范围.
七、(本题满分12分)
22、如图,直线y=2x+6与反比例函数(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线
y =n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM。
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6->0的解集;
(3)直线y =n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
八、(本题满分14分)
23、某服装批发市场销售一种衬衫,衬衫每件进价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫中获得24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫每件的利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值?最大利润是多少?
合肥瑶海区三十中2021-2022学年九上期中模拟数学试卷答案
1 2 3 4 5 6 7 8 9 10
A A D D B A B A A B
11、 直线x=2; 1<a≤2; 12、 0<y≤3; 13、 ; 14、 -16;
15、 (1) 直线x=2; (2)a=3; (3)≤a<2;
16、(1)a=-2.5、 b=-5、 k=-5; (2)(0,1)或(0,-7)
17、 当x+y+z≠0时,k=2或当x+y+z=0,即x+y=-z,k=-1;
18、EG=; FG=;
19、(1)10≤x≤28; (2)定价每包28元,最大利润15840元;
(1)y=-20x+2600; (2)定价为70元; (3)x=75时,w取最大值为27500元;
同课章节目录
