2021-2022学年山东省菏泽市牡丹学校九年级(上)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省菏泽市牡丹学校九年级(上)开学数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 21:25:20 | ||
图片预览



文档简介
2021-2022学年山东省菏泽市牡丹学校九年级(上)开学数学试卷
一、选择题(每小题3分)
1.(3分)下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )
A.厨余垃圾 B.可回收物
C.其他垃圾 D.有害垃圾
2.(3分)下列等式从左到右变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2 B.x2﹣2x+1=(x﹣1)2
C.2a﹣1=a(2﹣) D.x2+6x+8=x(x+6)+8
3.(3分)不等式组的解集是x>4,那么m的取值范围是( )
A.m≤4 B.m≥4 C.m<4 D.m=4
4.(3分)自带水杯已成为人们良好的健康卫生习惯.某公司为员工购买甲、乙两种型号的水杯,用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,已知甲种水杯的单价比乙种水杯的单价多15元.设甲种水杯的单价为x元( )
A. B.
C. D.
5.(3分)如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°( )
A.55° B.65° C.75° D.85°
6.(3分)已知,在Rt△ABC中,∠ACB=90°,E分别是AB,BC的中点,使得CF=AC,则AB的长为( )
A.8 B. C.4 D.
7.(3分)对于实数a,b定义运算“☆”如下:a☆b=ab2﹣ab,例如3☆2=3×22﹣3×2=6,则方程1☆x=2的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
8.(3分)如图,在 ABCD中,对角线BD⊥AD,AD=6,O为BD的中点,直线EO交CD于点F,连接DE( )
A.四边形DEBF为平行四边形
B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形
D.若AE=4.8,则四边形DEBF为正方形
二.填空题(每小题3分)
9.(3分)分解因式:3x3﹣3x= .
10.(3分)若关于x的分式方程有增根,则m的值为 .
11.(3分)“杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生.某村种植了杂交水稻2018年的平均亩产300千克,2020年平均亩产363千克,则此水稻亩产量的平均增长率为 .
12.(3分)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内的一点,那么AP的长为 .
三.解答题
13.(10分)解下列方程.
(1)4x2+6x﹣5=0(用配方法);
(2)2(x﹣3)2=x2﹣9.
14.(7分)解不等式组,并将其解集在数轴上表示出来.
15.(7分)先化简,再求值:1+÷,其中m=﹣.
16.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
17.(12分)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,使其销售价格不超过(1)中的售价
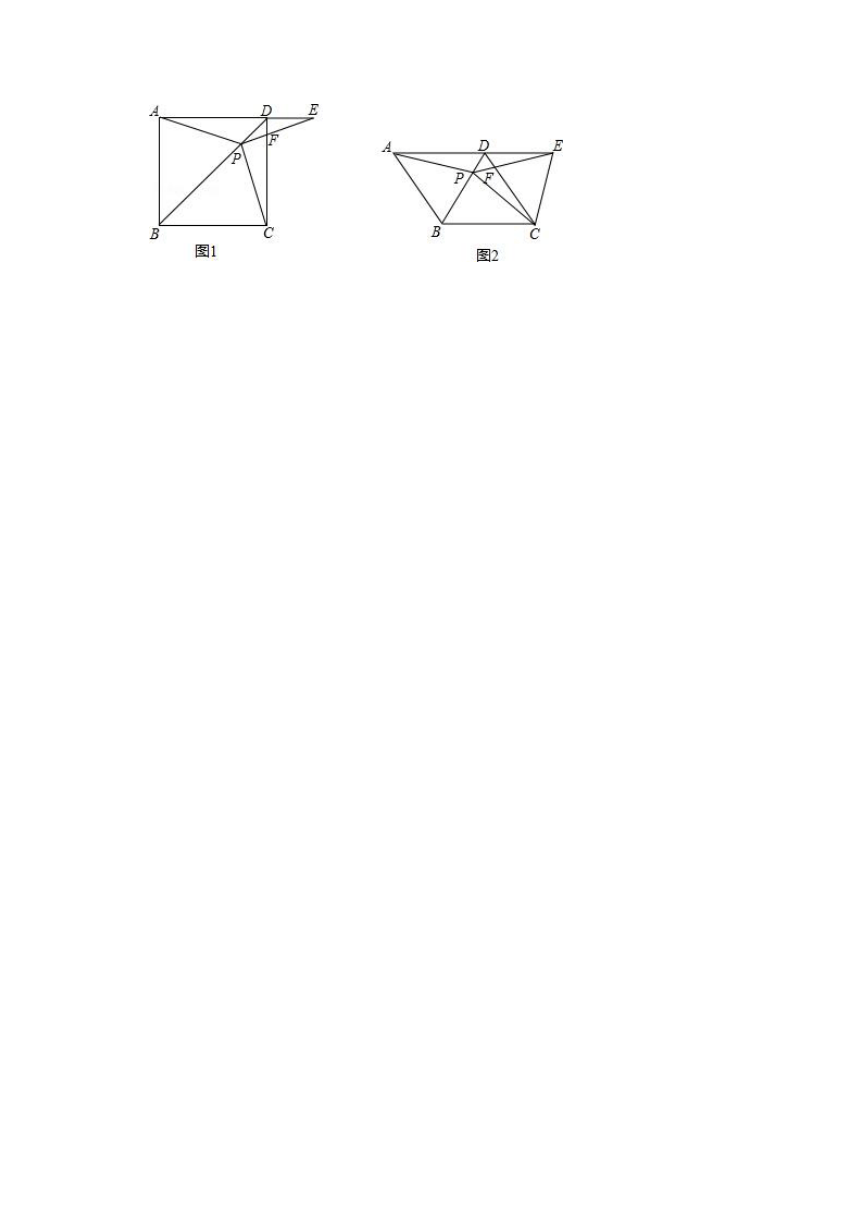
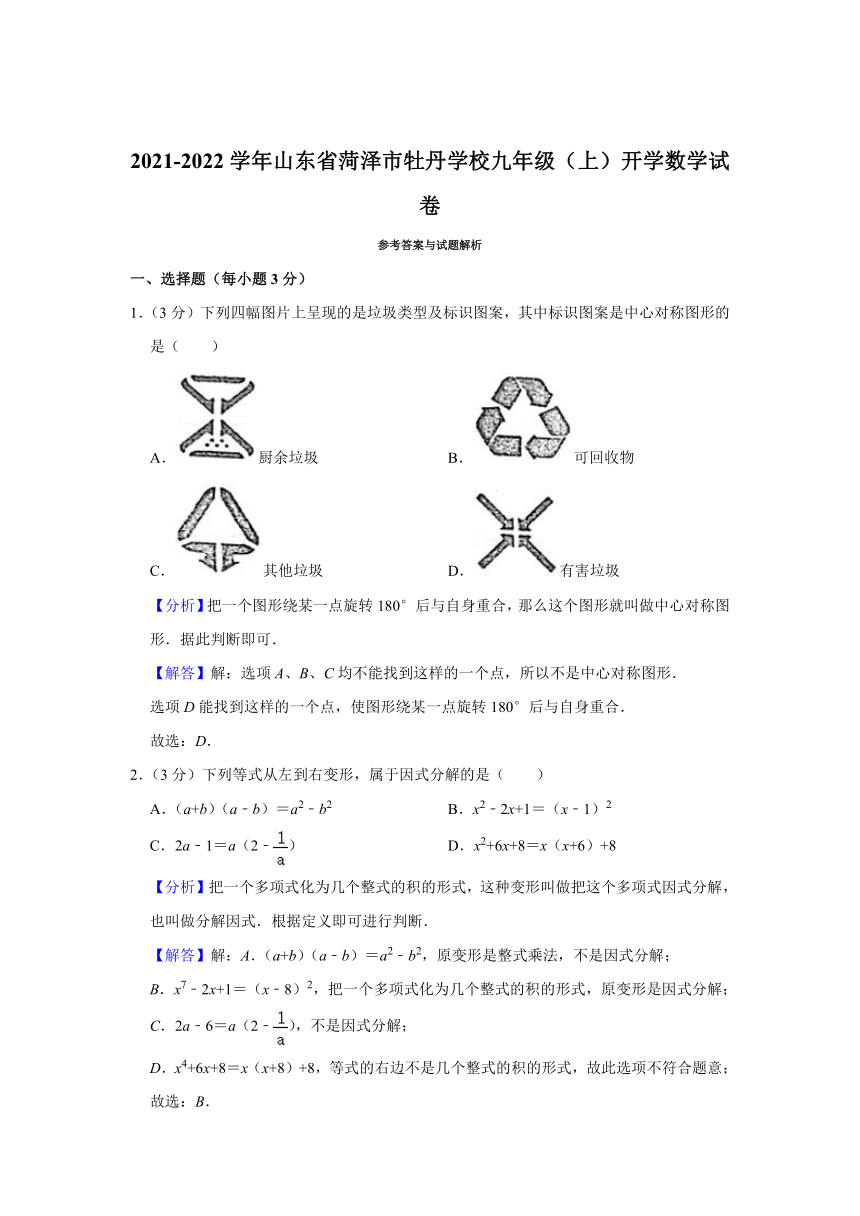
18.(16分)如图1,在正方形ABCD中,P是对角线BD上的一点,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,连接CE,试探究线段AP与线段CE的数量关系
2021-2022学年山东省菏泽市牡丹学校九年级(上)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分)
1.(3分)下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )
A.厨余垃圾 B.可回收物
C.其他垃圾 D.有害垃圾
【分析】把一个图形绕某一点旋转180°后与自身重合,那么这个图形就叫做中心对称图形.据此判断即可.
【解答】解:选项A、B、C均不能找到这样的一个点,所以不是中心对称图形.
选项D能找到这样的一个点,使图形绕某一点旋转180°后与自身重合.
故选:D.
2.(3分)下列等式从左到右变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2 B.x2﹣2x+1=(x﹣1)2
C.2a﹣1=a(2﹣) D.x2+6x+8=x(x+6)+8
【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据定义即可进行判断.
【解答】解:A.(a+b)(a﹣b)=a2﹣b2,原变形是整式乘法,不是因式分解;
B.x7﹣2x+1=(x﹣8)2,把一个多项式化为几个整式的积的形式,原变形是因式分解;
C.2a﹣6=a(2﹣),不是因式分解;
D.x4+6x+8=x(x+8)+8,等式的右边不是几个整式的积的形式,故此选项不符合题意;
故选:B.
3.(3分)不等式组的解集是x>4,那么m的取值范围是( )
A.m≤4 B.m≥4 C.m<4 D.m=4
【分析】先求出不等式的解集,再根据不等式组的解集得出答案即可.
【解答】解:,
解不等式①得:x>6,
∵不等式组的解集是x>3,
∴m≤4,
故选:A.
4.(3分)自带水杯已成为人们良好的健康卫生习惯.某公司为员工购买甲、乙两种型号的水杯,用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,已知甲种水杯的单价比乙种水杯的单价多15元.设甲种水杯的单价为x元( )
A. B.
C. D.
【分析】设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,利用数量=总价÷单价,结合用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,即可得出关于x的分式方程,此题得解.
【解答】解:设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,
依题意得:=.
故选:A.
5.(3分)如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°( )
A.55° B.65° C.75° D.85°
【分析】根据等腰直角三角形的性质求出∠FHE=45°,求出∠NHB=∠FHE=45°,根据三角形内角和定理求出∠HNB=105°,根据平行四边形的性质得出CD∥AB,根据平行线的性质得出∠2+∠HNB=180°,再求出答案即可.
【解答】解:延长EH交AB于N,
∵△EFH是等腰直角三角形,
∴∠FHE=45°,
∴∠NHB=∠FHE=45°,
∵∠1=30°,
∴∠HNB=180°﹣∠1﹣∠NHB=105°,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠8+∠HNB=180°,
∴∠2=75°,
故选:C.
6.(3分)已知,在Rt△ABC中,∠ACB=90°,E分别是AB,BC的中点,使得CF=AC,则AB的长为( )
A.8 B. C.4 D.
【分析】连接CD,证明四边形CDEF是平行四边形,则CD=EF=4,再利用直角三角形斜边上的中线性质可求AB长.
【解答】解:连接CD,
∵点D,E分别是AB,
∴DE∥AC,DE=.
∵延长AC到F,使得CF=,
∴DE∥CF且DE=CF,
∴四边形CDEF是平行四边形.
∴CD=EF=4.
∵∠ACB=90°,CD为斜边AB中线,
∴AB=5CD=8.
故选:A.
7.(3分)对于实数a,b定义运算“☆”如下:a☆b=ab2﹣ab,例如3☆2=3×22﹣3×2=6,则方程1☆x=2的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
【分析】根据运算“☆”的定义将方程1☆x=2转化为一般式,由根的判别式Δ=9>0,即可得出该方程有两个不相等的实数根.
【解答】解:∵1☆x=2,
∴6 x2﹣1 x=6,
∴x2﹣x﹣2=7,
∴Δ=(﹣1)2﹣3×1×(﹣2)=5>0,
∴方程1☆x=2有两个不相等的实数根.
故选:D.
8.(3分)如图,在 ABCD中,对角线BD⊥AD,AD=6,O为BD的中点,直线EO交CD于点F,连接DE( )
A.四边形DEBF为平行四边形
B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形
D.若AE=4.8,则四边形DEBF为正方形
【分析】根据平行四边形的判定方法,矩形的判定方法,菱形的判定方法,正方形的判定方法解答即可.
【解答】解:∵O为BD的中点,
∴OB=OD,
∵四边形ABCD为平行四边形,
∴DC∥AB,
∴∠CDO=∠EBO,∠DFO=∠OEB,
∴△FDO≌△EBO(AAS),
∴OE=OF,
∴四边形DEBF为平行四边形,
故A选项不符合题意,
若AE=3.6,AD=4,
∴,
又∵,
∴,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴∠AED=∠ADB=90°.
∴四边形DEBF为矩形.
故B选项不符合题意,
∵AB=10,AE=5,
∴BE=5,
又∵∠ADB=90°,
∴DE=AB=5,
∴DE=BE,
∴四边形DEBF为菱形.
故C选项不符合题意,
∵AE=3.3时,四边形DEBF为矩形,四边形DEBF为菱形,
∴AE=4.8时,四边形DEBF不可能是正方形.
故选项D符合题意.
故选:D.
二.填空题(每小题3分)
9.(3分)分解因式:3x3﹣3x= 3x(x﹣1)(x+1) .
【分析】首先提取公因式3x,再利用平方差公式分解因式得出答案.
【解答】解:3x3﹣4x
=3x(x2﹣4)
=3x(x﹣1)(x+3).
故答案为:3x(x﹣1)(x+6).
10.(3分)若关于x的分式方程有增根,则m的值为 4 .
【分析】首先把所给的分式方程化为整式方程,然后根据分式方程有增根,得到x﹣2=0,据此求出x的值,代入整式方程求出m的值即可.
【解答】解:去分母,得:2x=m+(x﹣2),
由分式方程有增根,得到x﹣7=0,
把x=2代入整式方程,可得:m=8.
故答案为:4.
11.(3分)“杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生.某村种植了杂交水稻2018年的平均亩产300千克,2020年平均亩产363千克,则此水稻亩产量的平均增长率为 10% .
【分析】设水稻亩产量的年平均增长率为x,根据“2018年平均亩产×1加增长率的平方=2020年平均亩产”即可列出关于x的一元二次方程,解方程即可得出结论.
【解答】解:设水稻亩产量的年平均增长率为x,
根据题意得:300×(1+x)2=363,
解得:x=10%或x=﹣210%(舍去).
答:水稻亩产量的年平均增长率为10%.
故答案为:10%.
12.(3分)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内的一点,那么AP的长为 3+1或3﹣1 .
【分析】此题要分两种情况:当P与A在BD的异侧时;当P与A在BD的同侧时,分别计算出AP长即可.
【解答】解:当P与A在BD的异侧时:连接AP交BD于M,
∵AD=AB,DP=BP,
∴AP⊥BD(到线段两端距离相等的点在垂直平分线上),
在直角△ABM中,∠BAM=30°,
∴AM=AB cos30°=3,BM=AB sin30°=3,
∴PM==2,
∴AP=AM+PM=3+4;
当P与A在BD的同侧时:连接AP并延长AP交BD于点M
AP=AM﹣PM=3﹣7;
当P与M重合时,PD=PB=3矛盾.
AP的长为3+1或3.
故答案为3+3或3.
三.解答题
13.(10分)解下列方程.
(1)4x2+6x﹣5=0(用配方法);
(2)2(x﹣3)2=x2﹣9.
【分析】(1)将常数项移到方程的右边,然后将二次项系数化为1,继而两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得;
(2)移项后利用因式分解法求解即可.
【解答】解:(1)∵4x2+6x﹣5=0,
移项得:8x2+6x=8;
系数化为1得:;
配方得:;
化简得:
解得:;;
(2)∵2(x﹣3)=(x+3)(x﹣6);
移项:2(x﹣3)﹣(x+3)(x﹣3)=0,
提取公因式:(x﹣3)(2x﹣6﹣x﹣6)=0,
化简:(x﹣3)(x﹣2)=0,
则:x﹣3=7或x﹣9=0,
解得:x4=3,x2=3.
14.(7分)解不等式组,并将其解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:解不等式﹣1<,
解不等式5x≥7x﹣3,得:x≤3,
则不等式组的解集为﹣6<x≤3,
将不等式组的解集表示在数轴上如下:
15.(7分)先化简,再求值:1+÷,其中m=﹣.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再由已知等式得出m=﹣n,代入、约分即可.
【解答】解:原式=1+
=1﹣
=﹣
=,
∵=﹣,
∴m=﹣n,
则原式===﹣6.
16.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
【解答】证明:(1)∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形.
17.(12分)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,使其销售价格不超过(1)中的售价
【分析】(1)根据日利润=每件利润×日销售量,可求出售价为60元时的原利润,设售价应定为x元,则每件的利润为(x﹣40)元,日销售量为20+=(140﹣2x)件,根据日利润=每件利润×日销售量,即可得出关于x的一元二次方程,解之取其较小值即可得出结论;
(2)设该商品需要打a折销售,根据销售价格不超过50元,列出不等式求解即可.
【解答】解:(1)设售价应定为x元,则每件的利润为(x﹣40)元=(140﹣2x)件,
依题意,得:(x﹣40)(140﹣5x)=(60﹣40)×20,
整理,得:x2﹣110x+3000=0,
解得:x2=50,x2=60(舍去).
答:售价应定为50元;
(2)该商品需要打a折销售,
由题意,得,62.5×,
解得:a≤7,
答:该商品至少需打8折销售.
18.(16分)如图1,在正方形ABCD中,P是对角线BD上的一点,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,连接CE,试探究线段AP与线段CE的数量关系
【分析】(1)欲证明PC=PE,只要证明△ABP≌△CBP即可;
(2)利用“8字型”证明角相等即可解决问题;
(3)首先证明△ABP≌△CBP(SAS)推出PA=PC,∠BAP=∠BCP,再证明△EPC是等边三角形,可得PC=CE,即可解决问题;
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,∴PC=PE,
∵PA=PE,∴∠DAP=∠DEP,
∵∠CFP=∠EFD,∴∠CPF=∠EDF
∵∠ABC=∠ADC=120°,
∴∠CPF=∠EDF=180°﹣∠ADC=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
一、选择题(每小题3分)
1.(3分)下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )
A.厨余垃圾 B.可回收物
C.其他垃圾 D.有害垃圾
2.(3分)下列等式从左到右变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2 B.x2﹣2x+1=(x﹣1)2
C.2a﹣1=a(2﹣) D.x2+6x+8=x(x+6)+8
3.(3分)不等式组的解集是x>4,那么m的取值范围是( )
A.m≤4 B.m≥4 C.m<4 D.m=4
4.(3分)自带水杯已成为人们良好的健康卫生习惯.某公司为员工购买甲、乙两种型号的水杯,用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,已知甲种水杯的单价比乙种水杯的单价多15元.设甲种水杯的单价为x元( )
A. B.
C. D.
5.(3分)如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°( )
A.55° B.65° C.75° D.85°
6.(3分)已知,在Rt△ABC中,∠ACB=90°,E分别是AB,BC的中点,使得CF=AC,则AB的长为( )
A.8 B. C.4 D.
7.(3分)对于实数a,b定义运算“☆”如下:a☆b=ab2﹣ab,例如3☆2=3×22﹣3×2=6,则方程1☆x=2的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
8.(3分)如图,在 ABCD中,对角线BD⊥AD,AD=6,O为BD的中点,直线EO交CD于点F,连接DE( )
A.四边形DEBF为平行四边形
B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形
D.若AE=4.8,则四边形DEBF为正方形
二.填空题(每小题3分)
9.(3分)分解因式:3x3﹣3x= .
10.(3分)若关于x的分式方程有增根,则m的值为 .
11.(3分)“杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生.某村种植了杂交水稻2018年的平均亩产300千克,2020年平均亩产363千克,则此水稻亩产量的平均增长率为 .
12.(3分)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内的一点,那么AP的长为 .
三.解答题
13.(10分)解下列方程.
(1)4x2+6x﹣5=0(用配方法);
(2)2(x﹣3)2=x2﹣9.
14.(7分)解不等式组,并将其解集在数轴上表示出来.
15.(7分)先化简,再求值:1+÷,其中m=﹣.
16.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
17.(12分)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,使其销售价格不超过(1)中的售价
18.(16分)如图1,在正方形ABCD中,P是对角线BD上的一点,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,连接CE,试探究线段AP与线段CE的数量关系
2021-2022学年山东省菏泽市牡丹学校九年级(上)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分)
1.(3分)下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )
A.厨余垃圾 B.可回收物
C.其他垃圾 D.有害垃圾
【分析】把一个图形绕某一点旋转180°后与自身重合,那么这个图形就叫做中心对称图形.据此判断即可.
【解答】解:选项A、B、C均不能找到这样的一个点,所以不是中心对称图形.
选项D能找到这样的一个点,使图形绕某一点旋转180°后与自身重合.
故选:D.
2.(3分)下列等式从左到右变形,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2 B.x2﹣2x+1=(x﹣1)2
C.2a﹣1=a(2﹣) D.x2+6x+8=x(x+6)+8
【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据定义即可进行判断.
【解答】解:A.(a+b)(a﹣b)=a2﹣b2,原变形是整式乘法,不是因式分解;
B.x7﹣2x+1=(x﹣8)2,把一个多项式化为几个整式的积的形式,原变形是因式分解;
C.2a﹣6=a(2﹣),不是因式分解;
D.x4+6x+8=x(x+8)+8,等式的右边不是几个整式的积的形式,故此选项不符合题意;
故选:B.
3.(3分)不等式组的解集是x>4,那么m的取值范围是( )
A.m≤4 B.m≥4 C.m<4 D.m=4
【分析】先求出不等式的解集,再根据不等式组的解集得出答案即可.
【解答】解:,
解不等式①得:x>6,
∵不等式组的解集是x>3,
∴m≤4,
故选:A.
4.(3分)自带水杯已成为人们良好的健康卫生习惯.某公司为员工购买甲、乙两种型号的水杯,用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,已知甲种水杯的单价比乙种水杯的单价多15元.设甲种水杯的单价为x元( )
A. B.
C. D.
【分析】设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,利用数量=总价÷单价,结合用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,即可得出关于x的分式方程,此题得解.
【解答】解:设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,
依题意得:=.
故选:A.
5.(3分)如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°( )
A.55° B.65° C.75° D.85°
【分析】根据等腰直角三角形的性质求出∠FHE=45°,求出∠NHB=∠FHE=45°,根据三角形内角和定理求出∠HNB=105°,根据平行四边形的性质得出CD∥AB,根据平行线的性质得出∠2+∠HNB=180°,再求出答案即可.
【解答】解:延长EH交AB于N,
∵△EFH是等腰直角三角形,
∴∠FHE=45°,
∴∠NHB=∠FHE=45°,
∵∠1=30°,
∴∠HNB=180°﹣∠1﹣∠NHB=105°,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠8+∠HNB=180°,
∴∠2=75°,
故选:C.
6.(3分)已知,在Rt△ABC中,∠ACB=90°,E分别是AB,BC的中点,使得CF=AC,则AB的长为( )
A.8 B. C.4 D.
【分析】连接CD,证明四边形CDEF是平行四边形,则CD=EF=4,再利用直角三角形斜边上的中线性质可求AB长.
【解答】解:连接CD,
∵点D,E分别是AB,
∴DE∥AC,DE=.
∵延长AC到F,使得CF=,
∴DE∥CF且DE=CF,
∴四边形CDEF是平行四边形.
∴CD=EF=4.
∵∠ACB=90°,CD为斜边AB中线,
∴AB=5CD=8.
故选:A.
7.(3分)对于实数a,b定义运算“☆”如下:a☆b=ab2﹣ab,例如3☆2=3×22﹣3×2=6,则方程1☆x=2的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
【分析】根据运算“☆”的定义将方程1☆x=2转化为一般式,由根的判别式Δ=9>0,即可得出该方程有两个不相等的实数根.
【解答】解:∵1☆x=2,
∴6 x2﹣1 x=6,
∴x2﹣x﹣2=7,
∴Δ=(﹣1)2﹣3×1×(﹣2)=5>0,
∴方程1☆x=2有两个不相等的实数根.
故选:D.
8.(3分)如图,在 ABCD中,对角线BD⊥AD,AD=6,O为BD的中点,直线EO交CD于点F,连接DE( )
A.四边形DEBF为平行四边形
B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形
D.若AE=4.8,则四边形DEBF为正方形
【分析】根据平行四边形的判定方法,矩形的判定方法,菱形的判定方法,正方形的判定方法解答即可.
【解答】解:∵O为BD的中点,
∴OB=OD,
∵四边形ABCD为平行四边形,
∴DC∥AB,
∴∠CDO=∠EBO,∠DFO=∠OEB,
∴△FDO≌△EBO(AAS),
∴OE=OF,
∴四边形DEBF为平行四边形,
故A选项不符合题意,
若AE=3.6,AD=4,
∴,
又∵,
∴,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴∠AED=∠ADB=90°.
∴四边形DEBF为矩形.
故B选项不符合题意,
∵AB=10,AE=5,
∴BE=5,
又∵∠ADB=90°,
∴DE=AB=5,
∴DE=BE,
∴四边形DEBF为菱形.
故C选项不符合题意,
∵AE=3.3时,四边形DEBF为矩形,四边形DEBF为菱形,
∴AE=4.8时,四边形DEBF不可能是正方形.
故选项D符合题意.
故选:D.
二.填空题(每小题3分)
9.(3分)分解因式:3x3﹣3x= 3x(x﹣1)(x+1) .
【分析】首先提取公因式3x,再利用平方差公式分解因式得出答案.
【解答】解:3x3﹣4x
=3x(x2﹣4)
=3x(x﹣1)(x+3).
故答案为:3x(x﹣1)(x+6).
10.(3分)若关于x的分式方程有增根,则m的值为 4 .
【分析】首先把所给的分式方程化为整式方程,然后根据分式方程有增根,得到x﹣2=0,据此求出x的值,代入整式方程求出m的值即可.
【解答】解:去分母,得:2x=m+(x﹣2),
由分式方程有增根,得到x﹣7=0,
把x=2代入整式方程,可得:m=8.
故答案为:4.
11.(3分)“杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生.某村种植了杂交水稻2018年的平均亩产300千克,2020年平均亩产363千克,则此水稻亩产量的平均增长率为 10% .
【分析】设水稻亩产量的年平均增长率为x,根据“2018年平均亩产×1加增长率的平方=2020年平均亩产”即可列出关于x的一元二次方程,解方程即可得出结论.
【解答】解:设水稻亩产量的年平均增长率为x,
根据题意得:300×(1+x)2=363,
解得:x=10%或x=﹣210%(舍去).
答:水稻亩产量的年平均增长率为10%.
故答案为:10%.
12.(3分)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内的一点,那么AP的长为 3+1或3﹣1 .
【分析】此题要分两种情况:当P与A在BD的异侧时;当P与A在BD的同侧时,分别计算出AP长即可.
【解答】解:当P与A在BD的异侧时:连接AP交BD于M,
∵AD=AB,DP=BP,
∴AP⊥BD(到线段两端距离相等的点在垂直平分线上),
在直角△ABM中,∠BAM=30°,
∴AM=AB cos30°=3,BM=AB sin30°=3,
∴PM==2,
∴AP=AM+PM=3+4;
当P与A在BD的同侧时:连接AP并延长AP交BD于点M
AP=AM﹣PM=3﹣7;
当P与M重合时,PD=PB=3矛盾.
AP的长为3+1或3.
故答案为3+3或3.
三.解答题
13.(10分)解下列方程.
(1)4x2+6x﹣5=0(用配方法);
(2)2(x﹣3)2=x2﹣9.
【分析】(1)将常数项移到方程的右边,然后将二次项系数化为1,继而两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得;
(2)移项后利用因式分解法求解即可.
【解答】解:(1)∵4x2+6x﹣5=0,
移项得:8x2+6x=8;
系数化为1得:;
配方得:;
化简得:
解得:;;
(2)∵2(x﹣3)=(x+3)(x﹣6);
移项:2(x﹣3)﹣(x+3)(x﹣3)=0,
提取公因式:(x﹣3)(2x﹣6﹣x﹣6)=0,
化简:(x﹣3)(x﹣2)=0,
则:x﹣3=7或x﹣9=0,
解得:x4=3,x2=3.
14.(7分)解不等式组,并将其解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:解不等式﹣1<,
解不等式5x≥7x﹣3,得:x≤3,
则不等式组的解集为﹣6<x≤3,
将不等式组的解集表示在数轴上如下:
15.(7分)先化简,再求值:1+÷,其中m=﹣.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再由已知等式得出m=﹣n,代入、约分即可.
【解答】解:原式=1+
=1﹣
=﹣
=,
∵=﹣,
∴m=﹣n,
则原式===﹣6.
16.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
【解答】证明:(1)∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形.
17.(12分)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,使其销售价格不超过(1)中的售价
【分析】(1)根据日利润=每件利润×日销售量,可求出售价为60元时的原利润,设售价应定为x元,则每件的利润为(x﹣40)元,日销售量为20+=(140﹣2x)件,根据日利润=每件利润×日销售量,即可得出关于x的一元二次方程,解之取其较小值即可得出结论;
(2)设该商品需要打a折销售,根据销售价格不超过50元,列出不等式求解即可.
【解答】解:(1)设售价应定为x元,则每件的利润为(x﹣40)元=(140﹣2x)件,
依题意,得:(x﹣40)(140﹣5x)=(60﹣40)×20,
整理,得:x2﹣110x+3000=0,
解得:x2=50,x2=60(舍去).
答:售价应定为50元;
(2)该商品需要打a折销售,
由题意,得,62.5×,
解得:a≤7,
答:该商品至少需打8折销售.
18.(16分)如图1,在正方形ABCD中,P是对角线BD上的一点,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,连接CE,试探究线段AP与线段CE的数量关系
【分析】(1)欲证明PC=PE,只要证明△ABP≌△CBP即可;
(2)利用“8字型”证明角相等即可解决问题;
(3)首先证明△ABP≌△CBP(SAS)推出PA=PC,∠BAP=∠BCP,再证明△EPC是等边三角形,可得PC=CE,即可解决问题;
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,∴PC=PE,
∵PA=PE,∴∠DAP=∠DEP,
∵∠CFP=∠EFD,∴∠CPF=∠EDF
∵∠ABC=∠ADC=120°,
∴∠CPF=∠EDF=180°﹣∠ADC=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
同课章节目录
