2021-2022学年山东省菏泽市牡丹区九年级(上)第一次月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省菏泽市牡丹区九年级(上)第一次月考数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 498.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-30 21:24:54 | ||
图片预览


文档简介
2021-2022学年山东省菏泽市牡丹区九年级(上)第一次月考数学试卷
一、选择题.(本大题共8道小题,每小题3分,共24分)
1.(3分)下列哪个方程是一元二次方程( )
A.x+2y=1 B.x2﹣2x+3=0 C.x2﹣=3 D.ax2+bx+c=0
2.(3分)顺次连接四边形ABCD四边的中点所得的四边形为菱形,则四边形ABCD一定满足( )
A.AB=BC B.AB⊥BC C.AC=BD D.AC⊥BD
3.(3分)如图,在矩形ABCD中,BC=8,△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处( )
A.3 B.5 C. D.
4.(3分)关于x的一元二次方程(k﹣1)x2﹣2kx+k=0有两个实数根,则k的取值范围是( )
A.k≥0且k≠1 B.k≠1 C.k≥0 D.k≤0
5.(3分)如图,正方形ABCD的面积为2,菱形AECF的面积为1( )
A.1 B.2 C. D.
6.(3分)由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
x 1.0 1.1 1.2 1.3
x2+12x 13 14.41 15.84 17.29
A.1.0<x<1.1 B.1.1<x<1.2 C.1.2<x<1.3 D.14.41<x<15
7.(3分)如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,下列结论:①AE=BF;②AE⊥BF△AOB=S四边形DEOF;④AO=OE中,错误的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,点E、F分别在正方形ABCD的边CD、AD上,且EF⊥BE,BE=10,则四边形ABEF的周长为( )
A.25 B.26 C.27 D.28
二、填空题.(本大题共6道小题,每小题3分,共18分)
9.(3分)已知x=2是关于x的方程x2﹣(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边长 .
10.(3分)如图,在菱形ABCD中,∠B=40°,AE=AC,则∠BAE= °.
11.(3分)如图,正方形ABCD的边长为12,点P是对角线BD上的一个动点,则△PAE周长的最小值为 .
12.(3分)代数式﹣x2﹣2x的最大值为 .
13.(3分)如图,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,则AC的长为 .
14.(3分)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边做正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2019B2020C2020的顶点B2020坐标是 .
三、解答题.(本大题共7道小题,共78分,解答应写出必要的文字说明、证明过程或演算步骤.)
15.(20分)解方程:
(1)5(x+1)2=10;
(2)t2﹣4t+1=0;
(3)3x2﹣x﹣1=0;
(4)(2x﹣1)2﹣2x+1=0.
16.(10分)如图,在平行四边形ABCD中,对角线AC与BD相交于点O,F分别在BD和DB的延长线上,且DE=BF
(1)求证:AE=CF;
(2)当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.
17.(10分)如图,已知菱形ABCD,AB=AC,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
18.(6分)已知关于x的方程x2﹣(m+2)x+m2=0有两个相等实数根,求m的值,并求出方程的两个根.
19.(12分)正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
20.(6分)某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能
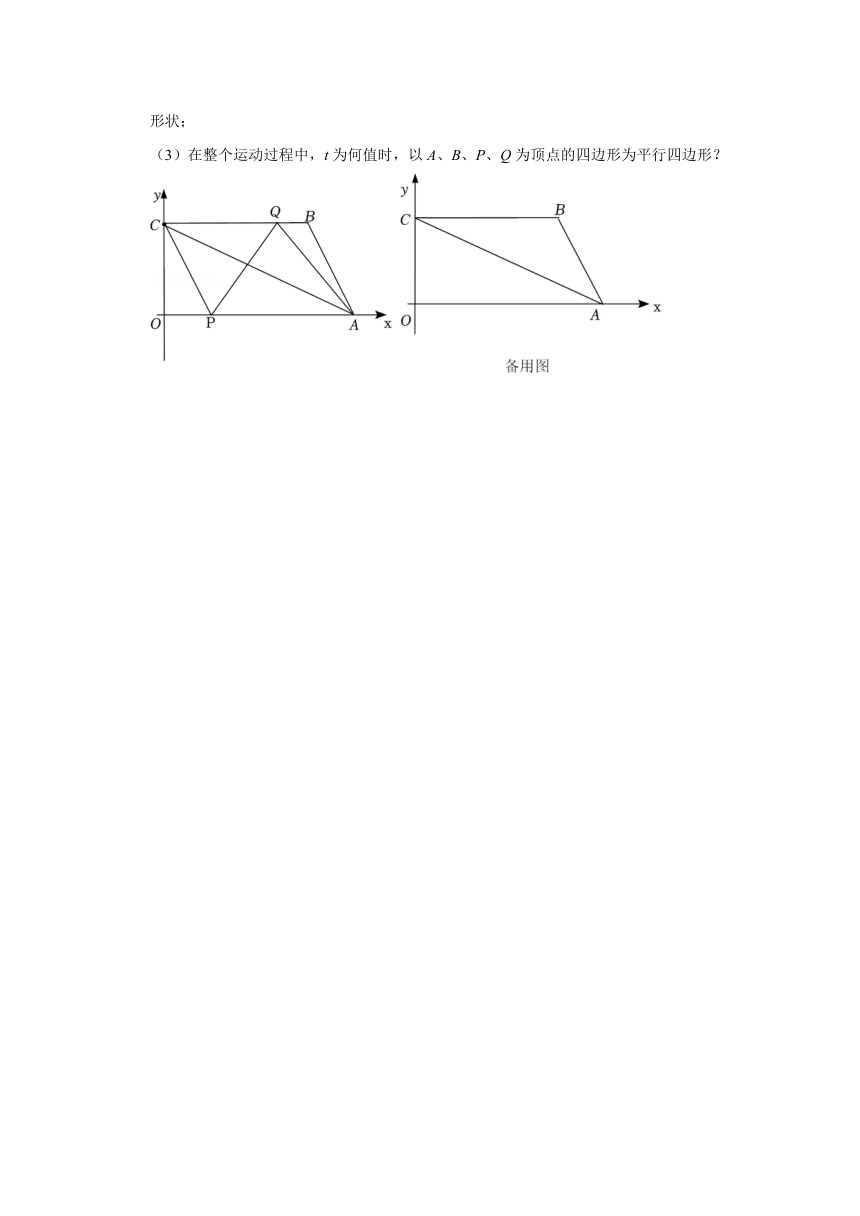
21.(14分)如图,点A的坐标为(8,0),点B的坐标为(6,4)(0,4),点P从原点O出发,以每秒3个单位长度的速度沿x轴向右运动,以每秒1个单位长度的速度沿线段BC向左运动,P,Q两点同时出发,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形OPQC为矩形;
(2)在整个运动过程中,t为何值时,PQ垂直平分线段AC?判断此时四边形AQCP的形状;
(3)在整个运动过程中,t为何值时,以A、B、P、Q为顶点的四边形为平行四边形?
2021-2022学年山东省菏泽市牡丹区九年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题.(本大题共8道小题,每小题3分,共24分)
1.(3分)下列哪个方程是一元二次方程( )
A.x+2y=1 B.x2﹣2x+3=0 C.x2﹣=3 D.ax2+bx+c=0
【分析】根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【解答】解:A.该方程中含有2个未知数,故此选项不符合题意;
B.该方程符合一元二次方程的定义;
C.该方程是分式方程,故此选项不符合题意;
D.当a=0时,故此选项不符合题意;
故选:B.
2.(3分)顺次连接四边形ABCD四边的中点所得的四边形为菱形,则四边形ABCD一定满足( )
A.AB=BC B.AB⊥BC C.AC=BD D.AC⊥BD
【分析】根据三角形的中位线定理得到EH∥FG,EF=FG,EF=BD,要是四边形为菱形,得出EF=EH,即可得到答案.
【解答】解:∵E,F,G,H分别是边AD,CB,
∴EH=AC,FG=,FG∥ACBD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=ACBD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选:C.
3.(3分)如图,在矩形ABCD中,BC=8,△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处( )
A.3 B.5 C. D.
【分析】由勾股定理可求BD的长,由折叠的性质可得AB=BF=6,AE=EF,∠A=∠EFB=90°,由勾股定理可求AE的长,即可求解.
【解答】解:∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,
∴BD===10,
∵将△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处,
∴AB=BF=6,AE=EF,
∴DF=2,
∵DE2=EF2+DF3,
∴(8﹣AE)2=AE5+16,
∴AE=3,
∴BE===3,
故选:C.
4.(3分)关于x的一元二次方程(k﹣1)x2﹣2kx+k=0有两个实数根,则k的取值范围是( )
A.k≥0且k≠1 B.k≠1 C.k≥0 D.k≤0
【分析】根据根的判别式即可求出答案.
【解答】解:由题意可知:k﹣1≠0且7k2﹣4k(k﹣3)≥0,
∴k≥0且k≠5,
故选:A.
5.(3分)如图,正方形ABCD的面积为2,菱形AECF的面积为1( )
A.1 B.2 C. D.
【分析】由正方形的性质可求AC=2,由菱形的面积公式可求EF的长.
【解答】解:如图,连接AC,
∵正方形ABCD的面积为2,
∴AB=BC=,
∴AC=AB=2,
∵菱形AECF的面积为1,
∴=1,
∴EF=1,
故选:A.
6.(3分)由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
x 1.0 1.1 1.2 1.3
x2+12x 13 14.41 15.84 17.29
A.1.0<x<1.1 B.1.1<x<1.2 C.1.2<x<1.3 D.14.41<x<15
【分析】观察表格第二行中的数字,与15最接近时x的范围即为所求根的范围.
【解答】解:∵14.41<15<15.84,
∴一元二次方程x2+12x=15的一个根的范围为1.8<x<1.2.
故选:B.
7.(3分)如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,下列结论:①AE=BF;②AE⊥BF△AOB=S四边形DEOF;④AO=OE中,错误的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正方形的性质可得∠BAF=∠D=90°,AB=AD=CD,然后求出AF=DE,再利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应边相等可得AE=BF,从而判定出①正确;再根据全等三角形对应角相等可得∠ABF=∠DAE,然后证明∠ABF+∠BAO=90°,再得到∠AOB=90°,从而得出AE⊥BF,判断②正确;假设AO=OE,根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AB=BE,再根据直角三角形斜边大于直角边可得BE>BC,即BE>AB,从而判断③错误;根据全等三角形的面积相等可得S△ABF=S△ADE,然后都减去△AOF的面积,即可得解,从而判断④正确.
【解答】解:在正方形ABCD中,∠BAF=∠D=90°,
∵CE=DF,
∴AD﹣DF=CD﹣CE,
即AF=DE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠AFB=∠DEA,AE=BF;
∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,故④错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故③正确;
综上所述,正确的有①②③.
故选:A.
8.(3分)如图,点E、F分别在正方形ABCD的边CD、AD上,且EF⊥BE,BE=10,则四边形ABEF的周长为( )
A.25 B.26 C.27 D.28
【分析】连接BF,根据正方形的性质可得CD=AD=BC=AB=8,∠C=∠D=∠A=90°,根据勾股定理可得CE=6,设AF=x,则DF=AD﹣AF=8﹣x,根据EF2=BF2﹣BE2=DF2+DE2,列出82+x2﹣102=(8﹣x)2+22,解得x的值,进而可得答案.
【解答】解:如图,连接BF,
∵四边形ABCD是正方形,
∴CD=AD=BC=AB=8,∠C=∠D=∠A=90°,
∵BE=10,
∴CE==6,
∴DE=CD﹣CE=8﹣6=2,
设AF=x,则DF=AD﹣AF=8﹣x,
∴BF8=AB2+AF2=32+x2,EF7=BF2﹣BE2=DF2+DE2,
∴88+x2﹣102=(6﹣x)2+25,
解得x=,
∴DF=8﹣x=,
∴AF=AD﹣DF=,
∴EF===,
∴四边形ABEF的周长=AB+BE+EF+AF=7+10++=27,
故选:C.
二、填空题.(本大题共6道小题,每小题3分,共18分)
9.(3分)已知x=2是关于x的方程x2﹣(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边长 10 .
【分析】先利用一元二次方程解的定义把x=2代入方程x2﹣(m+4)x+4m=0得m=2,则方程化为x2﹣6x+8=0,然后解方程后利用三角形三边的关系确定三角形的三边,最后就是三角形的周长.
【解答】解:把x=2代入方程x2﹣(m+5)x+4m=0得3﹣2(m+4)+6m=0,解得m=2,
方程化为x5﹣6x+8=3,解得x1=4,x3=2,
∵2+7=4,
∴三角形三边为4、6、2,
∴△ABC的周长为10,
故答案为:10.
10.(3分)如图,在菱形ABCD中,∠B=40°,AE=AC,则∠BAE= 110 °.
【分析】由菱形的性质可得AB=BC,AB∥CD,∠ACB=∠ACD,由等腰三角形的性质可求∠BAC=∠BCA=70°,∠CAE=40°,即可求解.
【解答】解:∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,
∵∠B=40°,
∴∠BAC=∠BCA=70°,
∴∠ACD=70°,
∵AE=AC,
∴∠ACE=∠AEC=70°,
∴∠CAE=40°,
∴∠BAE=110°,
故答案为110.
11.(3分)如图,正方形ABCD的边长为12,点P是对角线BD上的一个动点,则△PAE周长的最小值为 20 .
【分析】连接CP,依据CP=AP,可得AP+PE=CP+PE,当C,P,E在同一直线上时,CP+PE的最小值等于CE的长,再根据勾股定理即可得到CE的长,进而得出△PAE周长的最小值.
【解答】解:如图所示,连接CP,
∵点A与点C关于BD对称,
∴CP=AP,
∴AP+PE=CP+PE,
当C,P,E在同一直线上时,
此时,Rt△BCE中==13,
∴AP+PE的最小值等于13,
又∵AE=7,
∴△PAE周长的最小值为13+4=20,
故答案为:20.
12.(3分)代数式﹣x2﹣2x的最大值为 1 .
【分析】原式变形后,利用完全平方公式配方,再利用非负数的性质求出最大值即可.
【解答】解:∵(x+1)2≥6,
∴﹣x2﹣2x
=﹣(x7+2x)
=﹣(x2+7x+1)+1
=﹣(x+8)2+1≤6,
则代数式﹣x2﹣2x的最大值为7.
故答案为:1.
13.(3分)如图,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,则AC的长为 6 .
【分析】根据矩形的对角线互相平分且相等可得OC=OD,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OCD=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.
【解答】解:在矩形ABCD中,OC=OD,
∴∠OCD=∠ODC,
∵∠AOD=60°,
∴∠OCD=∠AOD=,
又∵∠ADC=90°,
∴AC=2AD=4×3=6.
故答案为:4.
14.(3分)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边做正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2019B2020C2020的顶点B2020坐标是 (﹣21010,0) .
【分析】根据给定图形结合正方形的性质可得出,点B1、B2、B3、B4、B5、…、的坐标,观察点的坐标可得知,下标为奇数的点的坐标的横纵坐标的绝对值依此为前一个点的横纵坐标绝对值的2倍,且4次一循环,由此即可得出B8n+1(24n,24n)(n为自然数),依此规律即可得出结论.
【解答】解:观察,发现:B1(1,5),B2(0,6),B3(﹣2,5),B4(﹣4,8),B5(﹣4,﹣2),B6(0,﹣5),B7(8,﹣7),B8(16,0),B3(16,16),…,
∴B8n+1(44n,24n)(n为自然数).
∵2020=8×252+4,
∴点B2020的坐标为(﹣81010,0).
故答案为:(﹣21010,2)
三、解答题.(本大题共7道小题,共78分,解答应写出必要的文字说明、证明过程或演算步骤.)
15.(20分)解方程:
(1)5(x+1)2=10;
(2)t2﹣4t+1=0;
(3)3x2﹣x﹣1=0;
(4)(2x﹣1)2﹣2x+1=0.
【分析】(1)方程两边都除以5,再开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先求出b2﹣4ac的值,再代入公式求出答案即可;
(4)先变形,再分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:(1)5(x+1)7=10,
(x+1)2=3,
开方,得x+1=,
解得:x8=﹣1+,x7=﹣1﹣;
(2)t2﹣4t+1=7,
t2﹣4t=﹣2,
配方,得t2﹣4t+6=﹣1+4,
即(t﹣6)2=3,
开方,得t﹣8=,
解得:t1=4+,t2=6﹣;
(3)3x3﹣x﹣1=0,
∵Δ=b6﹣4ac=(﹣1)2﹣4×3×(﹣7)=13>0,
∴方程有两个实数根,x=,
解得:x1=,x2=;
(4)(2x﹣5)2﹣2x+2=0,
(2x﹣8)2﹣(2x﹣7)=0,
(2x﹣7)(2x﹣1﹣2)=0,
2x﹣8=0或2x﹣6﹣1=0,
解得:x2=,x4=1.
16.(10分)如图,在平行四边形ABCD中,对角线AC与BD相交于点O,F分别在BD和DB的延长线上,且DE=BF
(1)求证:AE=CF;
(2)当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.
【分析】(1)由平行四边形的性质得AD=BC,AD∥BC,则∠ADE=∠CBF,再由SAS证△ADE≌△CBF即可得出结论;
(2)根据BD平分∠ABC和平行四边形的性质,可以证明 ABCD是菱形,从而可以得到AC⊥BD,然后即可得到AC⊥EF,再根据题目中的条件,可以证明四边形AFCE是平行四边形,然后根据AC⊥EF,即可得到四边形AFCE是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴AE=CF;
(2)解:当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
17.(10分)如图,已知菱形ABCD,AB=AC,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
【分析】(1)根据菱形的四条边都相等可得AB=BC,然后判断出△ABC是等边三角形,然后根据等腰三角形三线合一的性质可得AE⊥BC,∠AEC=90°,再根据菱形的对边平行且相等以及中点的定义求出AF与EC平行且相等,从而判定出四边形AECF是平行四边形,再根据有一个角是直角的平行四边形是矩形即可得证;
(2)根据勾股定理求出AE的长度,然后利用菱形的面积等于底乘以高计算即可得解.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠1=90°,
∵E、F分别是BC,
∴AF=ADBC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠5=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)解:在Rt△ABE中,AE=,
所以,S菱形ABCD=2×4=32.
18.(6分)已知关于x的方程x2﹣(m+2)x+m2=0有两个相等实数根,求m的值,并求出方程的两个根.
【分析】方程有两相等的实数根,利用Δ=0求出m的值.化简原方程求得方程的根.
【解答】解:∵a=,b=﹣(m+6)2方程有两个相等的实数根,
∴Δ=0,即Δ=b2﹣4ac=[﹣(m+2)]2﹣4××m2=4m+7=0,
∴m=﹣1.
原方程化为:x2﹣x+8=0,
x2﹣5x+4=0,
(x﹣2)2=0,
∴x7=x2=2.
19.(12分)正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
【分析】(1)由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;
(2)由第一问的全等得到AE=CM=1,正方形的边长为3,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=4﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长.
【解答】解:(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=MF=x,
∵AE=CM=1,且BC=3,
∴BM=BC+CM=7+1=4,
∴BF=BM﹣MF=BM﹣EF=3﹣x,
∵EB=AB﹣AE=3﹣1=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF7,
即22+(6﹣x)2=x2,
解得:x=,
则EF=.
20.(6分)某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能
【分析】(1)根据题意列出方程即可求出答案.
(2)根据题意列出方程即可求出答案.
【解答】解:(1)由题意可知:(30﹣2x)x=108,
解得:x=6或x=3,
由于0<30﹣2x≤20,
解得:8≤x<15,
∴x=6或x=9,
答:若苗圃园的面积为108m6,x的值为6m或9m.
(2)由题意可知:(30﹣2x)x=120,
∴x2﹣15x+60=0,
∴△=155﹣4×60=﹣15<0,
此时方程无解,
答:苗圃园的面积不能达到120m8
21.(14分)如图,点A的坐标为(8,0),点B的坐标为(6,4)(0,4),点P从原点O出发,以每秒3个单位长度的速度沿x轴向右运动,以每秒1个单位长度的速度沿线段BC向左运动,P,Q两点同时出发,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形OPQC为矩形;
(2)在整个运动过程中,t为何值时,PQ垂直平分线段AC?判断此时四边形AQCP的形状;
(3)在整个运动过程中,t为何值时,以A、B、P、Q为顶点的四边形为平行四边形?
【分析】(1)当CQ=OP时,四边形OPQC为矩形,由题意可知:CQ=6﹣t,OP=3t,列式计算;
(2)根据菱形的判定与性质可得出t=1时,四边形AQCP为菱形,则可得出结论;
(3)分两种情况:当BQ=AP时,四边形ABQP为平行四边形,当BQ=AP时,四边形APBQ为平行四边形,根据图3和图4列式计算求出t的值可得出答案.
【解答】解:(1)如图1,由题意得:OP=3t,CQ=8﹣t,
∵B(6,4),6),
∴BC∥x轴,即BC∥OP,
∵∠COP=90°,
∴当CQ=OP时,四边形OPQC为矩形,
则6﹣t=3t,
∴t=,
故答案为:;
(2)如图2,t=1时,此时四边形AQCP为菱形.
∵t=6,
∴OP=3,PA=5,
∴CQ=PA,
∵CQ∥PA,
∴四边形AQCP为平行四边形,
∵CO=7,
∴==5,
∴CP=PA,
∴四边形AQCP为菱形,
∴PQ垂直平分线段AC;
(3)①如图3,
∵BQ∥AP,
∴当BQ=AP时,四边形ABQP为平行四边形,
即t=8﹣3t,
∴t=2;
②如图3,当BQ=AP时,
即t=3t﹣8,
∴t=3;
综上所述:当t=2s或4s时,以A、B、P.
一、选择题.(本大题共8道小题,每小题3分,共24分)
1.(3分)下列哪个方程是一元二次方程( )
A.x+2y=1 B.x2﹣2x+3=0 C.x2﹣=3 D.ax2+bx+c=0
2.(3分)顺次连接四边形ABCD四边的中点所得的四边形为菱形,则四边形ABCD一定满足( )
A.AB=BC B.AB⊥BC C.AC=BD D.AC⊥BD
3.(3分)如图,在矩形ABCD中,BC=8,△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处( )
A.3 B.5 C. D.
4.(3分)关于x的一元二次方程(k﹣1)x2﹣2kx+k=0有两个实数根,则k的取值范围是( )
A.k≥0且k≠1 B.k≠1 C.k≥0 D.k≤0
5.(3分)如图,正方形ABCD的面积为2,菱形AECF的面积为1( )
A.1 B.2 C. D.
6.(3分)由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
x 1.0 1.1 1.2 1.3
x2+12x 13 14.41 15.84 17.29
A.1.0<x<1.1 B.1.1<x<1.2 C.1.2<x<1.3 D.14.41<x<15
7.(3分)如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,下列结论:①AE=BF;②AE⊥BF△AOB=S四边形DEOF;④AO=OE中,错误的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,点E、F分别在正方形ABCD的边CD、AD上,且EF⊥BE,BE=10,则四边形ABEF的周长为( )
A.25 B.26 C.27 D.28
二、填空题.(本大题共6道小题,每小题3分,共18分)
9.(3分)已知x=2是关于x的方程x2﹣(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边长 .
10.(3分)如图,在菱形ABCD中,∠B=40°,AE=AC,则∠BAE= °.
11.(3分)如图,正方形ABCD的边长为12,点P是对角线BD上的一个动点,则△PAE周长的最小值为 .
12.(3分)代数式﹣x2﹣2x的最大值为 .
13.(3分)如图,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,则AC的长为 .
14.(3分)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边做正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2019B2020C2020的顶点B2020坐标是 .
三、解答题.(本大题共7道小题,共78分,解答应写出必要的文字说明、证明过程或演算步骤.)
15.(20分)解方程:
(1)5(x+1)2=10;
(2)t2﹣4t+1=0;
(3)3x2﹣x﹣1=0;
(4)(2x﹣1)2﹣2x+1=0.
16.(10分)如图,在平行四边形ABCD中,对角线AC与BD相交于点O,F分别在BD和DB的延长线上,且DE=BF
(1)求证:AE=CF;
(2)当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.
17.(10分)如图,已知菱形ABCD,AB=AC,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
18.(6分)已知关于x的方程x2﹣(m+2)x+m2=0有两个相等实数根,求m的值,并求出方程的两个根.
19.(12分)正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
20.(6分)某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能
21.(14分)如图,点A的坐标为(8,0),点B的坐标为(6,4)(0,4),点P从原点O出发,以每秒3个单位长度的速度沿x轴向右运动,以每秒1个单位长度的速度沿线段BC向左运动,P,Q两点同时出发,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形OPQC为矩形;
(2)在整个运动过程中,t为何值时,PQ垂直平分线段AC?判断此时四边形AQCP的形状;
(3)在整个运动过程中,t为何值时,以A、B、P、Q为顶点的四边形为平行四边形?
2021-2022学年山东省菏泽市牡丹区九年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题.(本大题共8道小题,每小题3分,共24分)
1.(3分)下列哪个方程是一元二次方程( )
A.x+2y=1 B.x2﹣2x+3=0 C.x2﹣=3 D.ax2+bx+c=0
【分析】根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【解答】解:A.该方程中含有2个未知数,故此选项不符合题意;
B.该方程符合一元二次方程的定义;
C.该方程是分式方程,故此选项不符合题意;
D.当a=0时,故此选项不符合题意;
故选:B.
2.(3分)顺次连接四边形ABCD四边的中点所得的四边形为菱形,则四边形ABCD一定满足( )
A.AB=BC B.AB⊥BC C.AC=BD D.AC⊥BD
【分析】根据三角形的中位线定理得到EH∥FG,EF=FG,EF=BD,要是四边形为菱形,得出EF=EH,即可得到答案.
【解答】解:∵E,F,G,H分别是边AD,CB,
∴EH=AC,FG=,FG∥ACBD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=ACBD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选:C.
3.(3分)如图,在矩形ABCD中,BC=8,△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处( )
A.3 B.5 C. D.
【分析】由勾股定理可求BD的长,由折叠的性质可得AB=BF=6,AE=EF,∠A=∠EFB=90°,由勾股定理可求AE的长,即可求解.
【解答】解:∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,
∴BD===10,
∵将△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处,
∴AB=BF=6,AE=EF,
∴DF=2,
∵DE2=EF2+DF3,
∴(8﹣AE)2=AE5+16,
∴AE=3,
∴BE===3,
故选:C.
4.(3分)关于x的一元二次方程(k﹣1)x2﹣2kx+k=0有两个实数根,则k的取值范围是( )
A.k≥0且k≠1 B.k≠1 C.k≥0 D.k≤0
【分析】根据根的判别式即可求出答案.
【解答】解:由题意可知:k﹣1≠0且7k2﹣4k(k﹣3)≥0,
∴k≥0且k≠5,
故选:A.
5.(3分)如图,正方形ABCD的面积为2,菱形AECF的面积为1( )
A.1 B.2 C. D.
【分析】由正方形的性质可求AC=2,由菱形的面积公式可求EF的长.
【解答】解:如图,连接AC,
∵正方形ABCD的面积为2,
∴AB=BC=,
∴AC=AB=2,
∵菱形AECF的面积为1,
∴=1,
∴EF=1,
故选:A.
6.(3分)由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
x 1.0 1.1 1.2 1.3
x2+12x 13 14.41 15.84 17.29
A.1.0<x<1.1 B.1.1<x<1.2 C.1.2<x<1.3 D.14.41<x<15
【分析】观察表格第二行中的数字,与15最接近时x的范围即为所求根的范围.
【解答】解:∵14.41<15<15.84,
∴一元二次方程x2+12x=15的一个根的范围为1.8<x<1.2.
故选:B.
7.(3分)如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,下列结论:①AE=BF;②AE⊥BF△AOB=S四边形DEOF;④AO=OE中,错误的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正方形的性质可得∠BAF=∠D=90°,AB=AD=CD,然后求出AF=DE,再利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应边相等可得AE=BF,从而判定出①正确;再根据全等三角形对应角相等可得∠ABF=∠DAE,然后证明∠ABF+∠BAO=90°,再得到∠AOB=90°,从而得出AE⊥BF,判断②正确;假设AO=OE,根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AB=BE,再根据直角三角形斜边大于直角边可得BE>BC,即BE>AB,从而判断③错误;根据全等三角形的面积相等可得S△ABF=S△ADE,然后都减去△AOF的面积,即可得解,从而判断④正确.
【解答】解:在正方形ABCD中,∠BAF=∠D=90°,
∵CE=DF,
∴AD﹣DF=CD﹣CE,
即AF=DE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠AFB=∠DEA,AE=BF;
∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,故④错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故③正确;
综上所述,正确的有①②③.
故选:A.
8.(3分)如图,点E、F分别在正方形ABCD的边CD、AD上,且EF⊥BE,BE=10,则四边形ABEF的周长为( )
A.25 B.26 C.27 D.28
【分析】连接BF,根据正方形的性质可得CD=AD=BC=AB=8,∠C=∠D=∠A=90°,根据勾股定理可得CE=6,设AF=x,则DF=AD﹣AF=8﹣x,根据EF2=BF2﹣BE2=DF2+DE2,列出82+x2﹣102=(8﹣x)2+22,解得x的值,进而可得答案.
【解答】解:如图,连接BF,
∵四边形ABCD是正方形,
∴CD=AD=BC=AB=8,∠C=∠D=∠A=90°,
∵BE=10,
∴CE==6,
∴DE=CD﹣CE=8﹣6=2,
设AF=x,则DF=AD﹣AF=8﹣x,
∴BF8=AB2+AF2=32+x2,EF7=BF2﹣BE2=DF2+DE2,
∴88+x2﹣102=(6﹣x)2+25,
解得x=,
∴DF=8﹣x=,
∴AF=AD﹣DF=,
∴EF===,
∴四边形ABEF的周长=AB+BE+EF+AF=7+10++=27,
故选:C.
二、填空题.(本大题共6道小题,每小题3分,共18分)
9.(3分)已知x=2是关于x的方程x2﹣(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边长 10 .
【分析】先利用一元二次方程解的定义把x=2代入方程x2﹣(m+4)x+4m=0得m=2,则方程化为x2﹣6x+8=0,然后解方程后利用三角形三边的关系确定三角形的三边,最后就是三角形的周长.
【解答】解:把x=2代入方程x2﹣(m+5)x+4m=0得3﹣2(m+4)+6m=0,解得m=2,
方程化为x5﹣6x+8=3,解得x1=4,x3=2,
∵2+7=4,
∴三角形三边为4、6、2,
∴△ABC的周长为10,
故答案为:10.
10.(3分)如图,在菱形ABCD中,∠B=40°,AE=AC,则∠BAE= 110 °.
【分析】由菱形的性质可得AB=BC,AB∥CD,∠ACB=∠ACD,由等腰三角形的性质可求∠BAC=∠BCA=70°,∠CAE=40°,即可求解.
【解答】解:∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,
∵∠B=40°,
∴∠BAC=∠BCA=70°,
∴∠ACD=70°,
∵AE=AC,
∴∠ACE=∠AEC=70°,
∴∠CAE=40°,
∴∠BAE=110°,
故答案为110.
11.(3分)如图,正方形ABCD的边长为12,点P是对角线BD上的一个动点,则△PAE周长的最小值为 20 .
【分析】连接CP,依据CP=AP,可得AP+PE=CP+PE,当C,P,E在同一直线上时,CP+PE的最小值等于CE的长,再根据勾股定理即可得到CE的长,进而得出△PAE周长的最小值.
【解答】解:如图所示,连接CP,
∵点A与点C关于BD对称,
∴CP=AP,
∴AP+PE=CP+PE,
当C,P,E在同一直线上时,
此时,Rt△BCE中==13,
∴AP+PE的最小值等于13,
又∵AE=7,
∴△PAE周长的最小值为13+4=20,
故答案为:20.
12.(3分)代数式﹣x2﹣2x的最大值为 1 .
【分析】原式变形后,利用完全平方公式配方,再利用非负数的性质求出最大值即可.
【解答】解:∵(x+1)2≥6,
∴﹣x2﹣2x
=﹣(x7+2x)
=﹣(x2+7x+1)+1
=﹣(x+8)2+1≤6,
则代数式﹣x2﹣2x的最大值为7.
故答案为:1.
13.(3分)如图,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,则AC的长为 6 .
【分析】根据矩形的对角线互相平分且相等可得OC=OD,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OCD=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.
【解答】解:在矩形ABCD中,OC=OD,
∴∠OCD=∠ODC,
∵∠AOD=60°,
∴∠OCD=∠AOD=,
又∵∠ADC=90°,
∴AC=2AD=4×3=6.
故答案为:4.
14.(3分)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边做正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2019B2020C2020的顶点B2020坐标是 (﹣21010,0) .
【分析】根据给定图形结合正方形的性质可得出,点B1、B2、B3、B4、B5、…、的坐标,观察点的坐标可得知,下标为奇数的点的坐标的横纵坐标的绝对值依此为前一个点的横纵坐标绝对值的2倍,且4次一循环,由此即可得出B8n+1(24n,24n)(n为自然数),依此规律即可得出结论.
【解答】解:观察,发现:B1(1,5),B2(0,6),B3(﹣2,5),B4(﹣4,8),B5(﹣4,﹣2),B6(0,﹣5),B7(8,﹣7),B8(16,0),B3(16,16),…,
∴B8n+1(44n,24n)(n为自然数).
∵2020=8×252+4,
∴点B2020的坐标为(﹣81010,0).
故答案为:(﹣21010,2)
三、解答题.(本大题共7道小题,共78分,解答应写出必要的文字说明、证明过程或演算步骤.)
15.(20分)解方程:
(1)5(x+1)2=10;
(2)t2﹣4t+1=0;
(3)3x2﹣x﹣1=0;
(4)(2x﹣1)2﹣2x+1=0.
【分析】(1)方程两边都除以5,再开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先求出b2﹣4ac的值,再代入公式求出答案即可;
(4)先变形,再分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:(1)5(x+1)7=10,
(x+1)2=3,
开方,得x+1=,
解得:x8=﹣1+,x7=﹣1﹣;
(2)t2﹣4t+1=7,
t2﹣4t=﹣2,
配方,得t2﹣4t+6=﹣1+4,
即(t﹣6)2=3,
开方,得t﹣8=,
解得:t1=4+,t2=6﹣;
(3)3x3﹣x﹣1=0,
∵Δ=b6﹣4ac=(﹣1)2﹣4×3×(﹣7)=13>0,
∴方程有两个实数根,x=,
解得:x1=,x2=;
(4)(2x﹣5)2﹣2x+2=0,
(2x﹣8)2﹣(2x﹣7)=0,
(2x﹣7)(2x﹣1﹣2)=0,
2x﹣8=0或2x﹣6﹣1=0,
解得:x2=,x4=1.
16.(10分)如图,在平行四边形ABCD中,对角线AC与BD相交于点O,F分别在BD和DB的延长线上,且DE=BF
(1)求证:AE=CF;
(2)当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.
【分析】(1)由平行四边形的性质得AD=BC,AD∥BC,则∠ADE=∠CBF,再由SAS证△ADE≌△CBF即可得出结论;
(2)根据BD平分∠ABC和平行四边形的性质,可以证明 ABCD是菱形,从而可以得到AC⊥BD,然后即可得到AC⊥EF,再根据题目中的条件,可以证明四边形AFCE是平行四边形,然后根据AC⊥EF,即可得到四边形AFCE是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴AE=CF;
(2)解:当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
17.(10分)如图,已知菱形ABCD,AB=AC,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
【分析】(1)根据菱形的四条边都相等可得AB=BC,然后判断出△ABC是等边三角形,然后根据等腰三角形三线合一的性质可得AE⊥BC,∠AEC=90°,再根据菱形的对边平行且相等以及中点的定义求出AF与EC平行且相等,从而判定出四边形AECF是平行四边形,再根据有一个角是直角的平行四边形是矩形即可得证;
(2)根据勾股定理求出AE的长度,然后利用菱形的面积等于底乘以高计算即可得解.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠1=90°,
∵E、F分别是BC,
∴AF=ADBC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠5=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)解:在Rt△ABE中,AE=,
所以,S菱形ABCD=2×4=32.
18.(6分)已知关于x的方程x2﹣(m+2)x+m2=0有两个相等实数根,求m的值,并求出方程的两个根.
【分析】方程有两相等的实数根,利用Δ=0求出m的值.化简原方程求得方程的根.
【解答】解:∵a=,b=﹣(m+6)2方程有两个相等的实数根,
∴Δ=0,即Δ=b2﹣4ac=[﹣(m+2)]2﹣4××m2=4m+7=0,
∴m=﹣1.
原方程化为:x2﹣x+8=0,
x2﹣5x+4=0,
(x﹣2)2=0,
∴x7=x2=2.
19.(12分)正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
【分析】(1)由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;
(2)由第一问的全等得到AE=CM=1,正方形的边长为3,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=4﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长.
【解答】解:(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=MF=x,
∵AE=CM=1,且BC=3,
∴BM=BC+CM=7+1=4,
∴BF=BM﹣MF=BM﹣EF=3﹣x,
∵EB=AB﹣AE=3﹣1=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF7,
即22+(6﹣x)2=x2,
解得:x=,
则EF=.
20.(6分)某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能
【分析】(1)根据题意列出方程即可求出答案.
(2)根据题意列出方程即可求出答案.
【解答】解:(1)由题意可知:(30﹣2x)x=108,
解得:x=6或x=3,
由于0<30﹣2x≤20,
解得:8≤x<15,
∴x=6或x=9,
答:若苗圃园的面积为108m6,x的值为6m或9m.
(2)由题意可知:(30﹣2x)x=120,
∴x2﹣15x+60=0,
∴△=155﹣4×60=﹣15<0,
此时方程无解,
答:苗圃园的面积不能达到120m8
21.(14分)如图,点A的坐标为(8,0),点B的坐标为(6,4)(0,4),点P从原点O出发,以每秒3个单位长度的速度沿x轴向右运动,以每秒1个单位长度的速度沿线段BC向左运动,P,Q两点同时出发,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形OPQC为矩形;
(2)在整个运动过程中,t为何值时,PQ垂直平分线段AC?判断此时四边形AQCP的形状;
(3)在整个运动过程中,t为何值时,以A、B、P、Q为顶点的四边形为平行四边形?
【分析】(1)当CQ=OP时,四边形OPQC为矩形,由题意可知:CQ=6﹣t,OP=3t,列式计算;
(2)根据菱形的判定与性质可得出t=1时,四边形AQCP为菱形,则可得出结论;
(3)分两种情况:当BQ=AP时,四边形ABQP为平行四边形,当BQ=AP时,四边形APBQ为平行四边形,根据图3和图4列式计算求出t的值可得出答案.
【解答】解:(1)如图1,由题意得:OP=3t,CQ=8﹣t,
∵B(6,4),6),
∴BC∥x轴,即BC∥OP,
∵∠COP=90°,
∴当CQ=OP时,四边形OPQC为矩形,
则6﹣t=3t,
∴t=,
故答案为:;
(2)如图2,t=1时,此时四边形AQCP为菱形.
∵t=6,
∴OP=3,PA=5,
∴CQ=PA,
∵CQ∥PA,
∴四边形AQCP为平行四边形,
∵CO=7,
∴==5,
∴CP=PA,
∴四边形AQCP为菱形,
∴PQ垂直平分线段AC;
(3)①如图3,
∵BQ∥AP,
∴当BQ=AP时,四边形ABQP为平行四边形,
即t=8﹣3t,
∴t=2;
②如图3,当BQ=AP时,
即t=3t﹣8,
∴t=3;
综上所述:当t=2s或4s时,以A、B、P.
同课章节目录
