4.2线段、射线、直线 第1课时 湘教版数学七年级上册 课件(共22张PPT)
文档属性
| 名称 | 4.2线段、射线、直线 第1课时 湘教版数学七年级上册 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 807.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 10:28:49 | ||
图片预览






文档简介
(共22张PPT)
4.2 线段、射线、直线
第4章 图形的认识
第1课时
(1)有始有终——打一线名称。
(2)有始无终——打一线名称。
(3)无始无终——打一线名称。
猜谜语
学习目标
1.在现实情境中理解线段、射线、直线的概念及它们的区别与联系.(重点)
2.会用不同的方法表示线段、射线、直线.(难点)
3.了解“两点确定一条直线”的几何事实.
导入新课
情境导入
讲授新课
线段、射线、直线的概念及表示方法
一
自主导学
1.生活中绷紧的琴弦、人行横道线都可以近似的看成 ,线段有 个端点。
2.将线段 就形成了射线, 所出的光线都可以近似的看做射线,射线有 个端点,可向 延伸。
3.将线段 就形成了直线, 可以近似的看做直线,直线有 个端点,可向 延伸。
综上所述:1.线段有 个端点 ,长度有限,可以度量
2.射线有 个端点, 长度无限,无法度量
3.直线有 个端点,长度无限,无法度量
线段
2
向一个方向无限延长
手电筒
1
向两个方向无限延长
笔直的铁轨
0
一方
两方
2
1
0
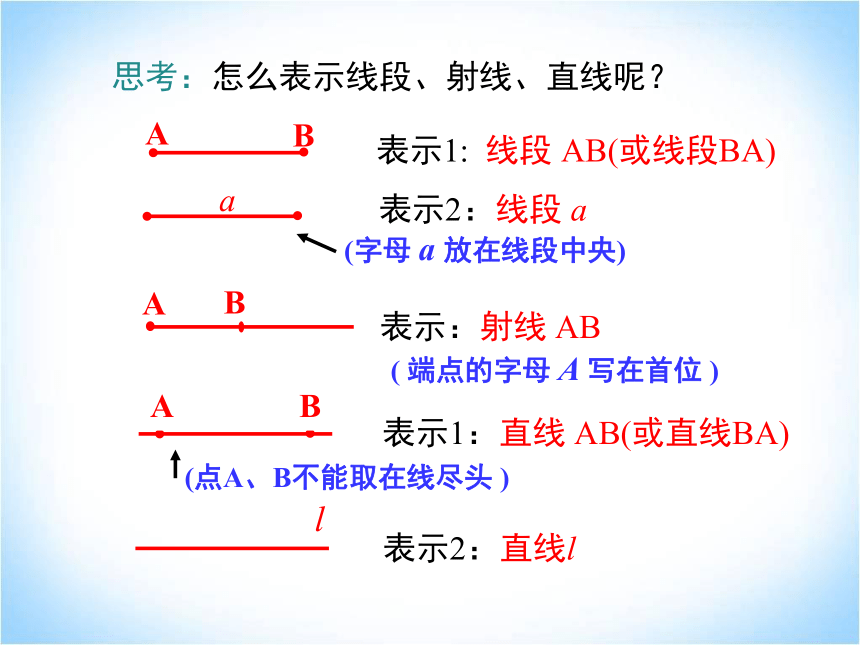
A
B
表示1: 线段 AB(或线段BA)
a
表示2:线段 a
表示:射线 AB
A
B
表示1:直线 AB(或直线BA)
表示2:直线l
l
思考:怎么表示线段、射线、直线呢?
( 端点的字母 A 写在首位 )
(点A、B不能取在线尽头 )
(字母 a 放在线段中央)
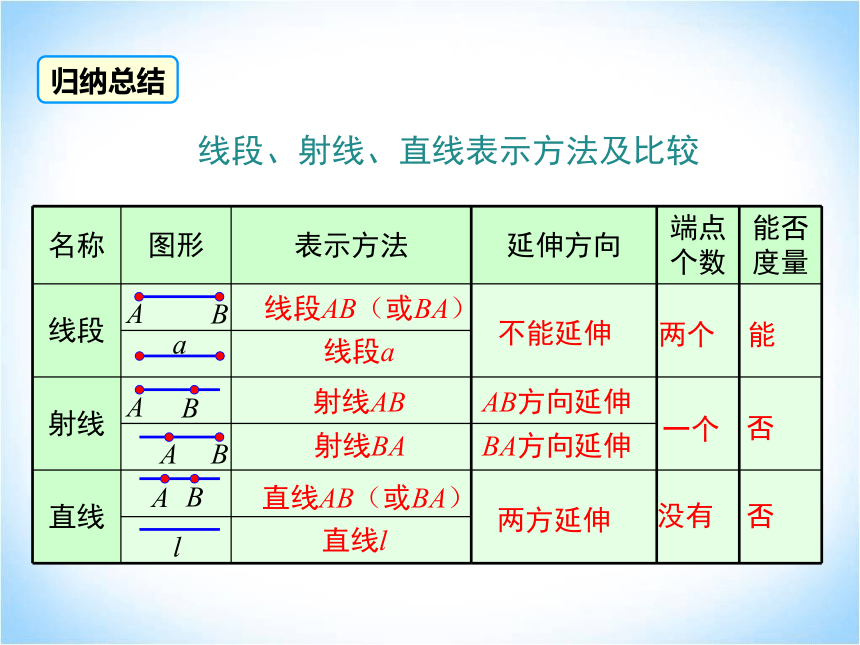
名称 图形 表示方法 延伸方向 端点个数 能否度量
线段
射线
直线
A
B
a
A
B
A
B
A
B
l
直线l
直线AB(或BA)
射线BA
射线AB
线段a
线段AB(或BA)
不能延伸
两个
能
AB方向延伸
一个
否
两方延伸
没有
否
BA方向延伸
归纳总结
线段、射线、直线表示方法及比较
点与直线的位置关系
二
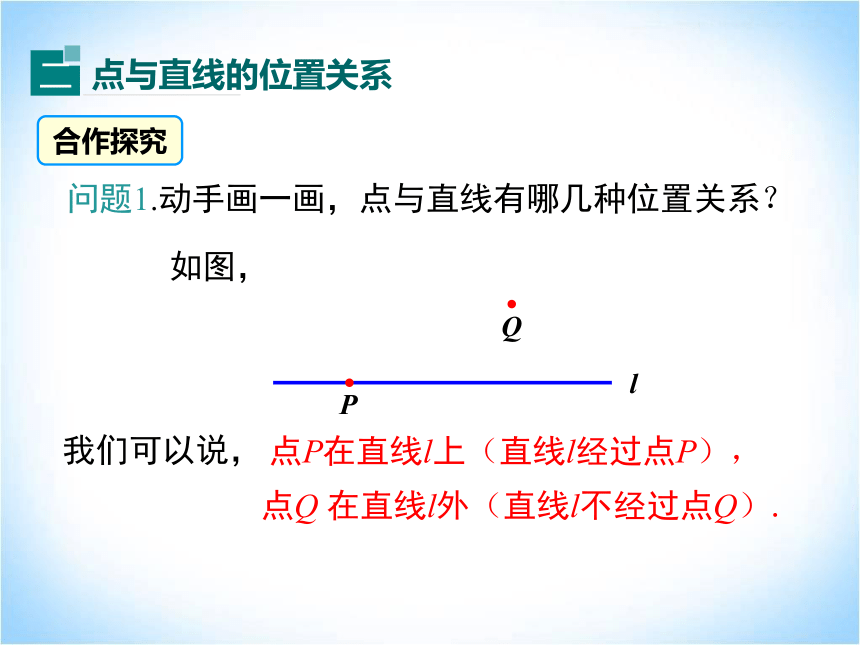
问题1.动手画一画,点与直线有哪几种位置关系?
合作探究
问题2. 画出直线AB与直线BC,它们有几个公共点?
问题3. (1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
点与直线的位置关系
二
问题1.动手画一画,点与直线有哪几种位置关系?
如图,
Q
l
P
点Q 在直线l外(直线l不经过点Q).
点P在直线l上(直线l经过点P),
我们可以说,
合作探究
问题2.如图,画出直线AB与直线BC,它们有几个公共点?
结论:当两条不同的直线只有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
合作探究
两点确定一条直线
三
问题三:(1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
·O
·A
·B
结论:经过两点有且只有一条直线.
合作探究
活动1:图中共有几条线段?说明你分析这个问题的具体思路;
合作探究
以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
点与直线有两种位置关系:点在直线上或点在直线外,也可以说直线经过这个点或直线不经过这个点.
如图,点P在直线l上(直线l经过点P),
l
点Q 在直线l外(直线l不经过点Q).
活动2:点与直线的位置关系
动手画一画,点与直线有哪几种位置关系?
合作探究
当两条不同的直线只有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
如图,直线l1与l2相交于点O.
1.如果你想将一根细木条固定在墙上,至少需要几个钉子?
活动3:直线的性质
合作探究
结论:
A
B
过两点有且只有一条直线.
或简述为:
两点确定一条直线.
植树时,只要定出两个树坑的位置,就能确定同一行的树坑所在的直线.
应用
1. 如图,判断下列语句是否正确?
(1)点O在直线AB上;
(2)点B是直线AB的一个端点;
(3)点O在射线AB上.
答:正确
答:不正确(因为直线没有端点)
答:不正确(因为射线AB是以A为端点)
(4) 射线AO和射线OA是同一条射线.
答:不正确(因为射线AO以A为端点,OA以O为端点)
课堂练习
2. 按下列语句分别画出图形:
(1)点P在直线l外;
(2)以O为端点的三条射线OA,OB,OC;
l
P
(3)点C在线段AB上.
O
A
B
C
A
B
C
(1)直线EF经过点C;
3. 按下列语句画出图形.
E
F
C
(2)经过点O的三条线段a,b,c;
(3)线段AB,CD相交于点B.
o
b
c
a
C
D
B
A
课堂小结
线段、射线、直线
线段、射线、直线的概念及表示
点与直线的位置关系:点在直线上;点在直线外
直线的基本事实:两点确定一条直线
4.2 线段、射线、直线
第4章 图形的认识
第1课时
(1)有始有终——打一线名称。
(2)有始无终——打一线名称。
(3)无始无终——打一线名称。
猜谜语
学习目标
1.在现实情境中理解线段、射线、直线的概念及它们的区别与联系.(重点)
2.会用不同的方法表示线段、射线、直线.(难点)
3.了解“两点确定一条直线”的几何事实.
导入新课
情境导入
讲授新课
线段、射线、直线的概念及表示方法
一
自主导学
1.生活中绷紧的琴弦、人行横道线都可以近似的看成 ,线段有 个端点。
2.将线段 就形成了射线, 所出的光线都可以近似的看做射线,射线有 个端点,可向 延伸。
3.将线段 就形成了直线, 可以近似的看做直线,直线有 个端点,可向 延伸。
综上所述:1.线段有 个端点 ,长度有限,可以度量
2.射线有 个端点, 长度无限,无法度量
3.直线有 个端点,长度无限,无法度量
线段
2
向一个方向无限延长
手电筒
1
向两个方向无限延长
笔直的铁轨
0
一方
两方
2
1
0
A
B
表示1: 线段 AB(或线段BA)
a
表示2:线段 a
表示:射线 AB
A
B
表示1:直线 AB(或直线BA)
表示2:直线l
l
思考:怎么表示线段、射线、直线呢?
( 端点的字母 A 写在首位 )
(点A、B不能取在线尽头 )
(字母 a 放在线段中央)
名称 图形 表示方法 延伸方向 端点个数 能否度量
线段
射线
直线
A
B
a
A
B
A
B
A
B
l
直线l
直线AB(或BA)
射线BA
射线AB
线段a
线段AB(或BA)
不能延伸
两个
能
AB方向延伸
一个
否
两方延伸
没有
否
BA方向延伸
归纳总结
线段、射线、直线表示方法及比较
点与直线的位置关系
二
问题1.动手画一画,点与直线有哪几种位置关系?
合作探究
问题2. 画出直线AB与直线BC,它们有几个公共点?
问题3. (1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
点与直线的位置关系
二
问题1.动手画一画,点与直线有哪几种位置关系?
如图,
Q
l
P
点Q 在直线l外(直线l不经过点Q).
点P在直线l上(直线l经过点P),
我们可以说,
合作探究
问题2.如图,画出直线AB与直线BC,它们有几个公共点?
结论:当两条不同的直线只有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
合作探究
两点确定一条直线
三
问题三:(1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
·O
·A
·B
结论:经过两点有且只有一条直线.
合作探究
活动1:图中共有几条线段?说明你分析这个问题的具体思路;
合作探究
以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
点与直线有两种位置关系:点在直线上或点在直线外,也可以说直线经过这个点或直线不经过这个点.
如图,点P在直线l上(直线l经过点P),
l
点Q 在直线l外(直线l不经过点Q).
活动2:点与直线的位置关系
动手画一画,点与直线有哪几种位置关系?
合作探究
当两条不同的直线只有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
如图,直线l1与l2相交于点O.
1.如果你想将一根细木条固定在墙上,至少需要几个钉子?
活动3:直线的性质
合作探究
结论:
A
B
过两点有且只有一条直线.
或简述为:
两点确定一条直线.
植树时,只要定出两个树坑的位置,就能确定同一行的树坑所在的直线.
应用
1. 如图,判断下列语句是否正确?
(1)点O在直线AB上;
(2)点B是直线AB的一个端点;
(3)点O在射线AB上.
答:正确
答:不正确(因为直线没有端点)
答:不正确(因为射线AB是以A为端点)
(4) 射线AO和射线OA是同一条射线.
答:不正确(因为射线AO以A为端点,OA以O为端点)
课堂练习
2. 按下列语句分别画出图形:
(1)点P在直线l外;
(2)以O为端点的三条射线OA,OB,OC;
l
P
(3)点C在线段AB上.
O
A
B
C
A
B
C
(1)直线EF经过点C;
3. 按下列语句画出图形.
E
F
C
(2)经过点O的三条线段a,b,c;
(3)线段AB,CD相交于点B.
o
b
c
a
C
D
B
A
课堂小结
线段、射线、直线
线段、射线、直线的概念及表示
点与直线的位置关系:点在直线上;点在直线外
直线的基本事实:两点确定一条直线
同课章节目录
