2021-2022学年 人教版八年级数学上册13.4最短路径问题课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年 人教版八年级数学上册13.4最短路径问题课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 799.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-31 13:23:28 | ||
图片预览



文档简介
(共17张PPT)
最短路径(将军饮马)问题
13.4 课题学习
教学内容分析:
最短路径问题在现实生活中经常遇到,初中阶段主要以“两点之间线段最短”“连接直线外一点与直线上各点的所有线段中,垂线段最短”为基础知识进行研究,本节以“牧马人饮马” 问题为载体开展对“最短路径”的课题研究让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”。
教学目标:
能利用轴对称解决简单的最短路径问题,在探究的过中体会轴对称的桥梁作用,感悟转化的数学思想。
如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
想想这个题用了什么原理求线段的最短
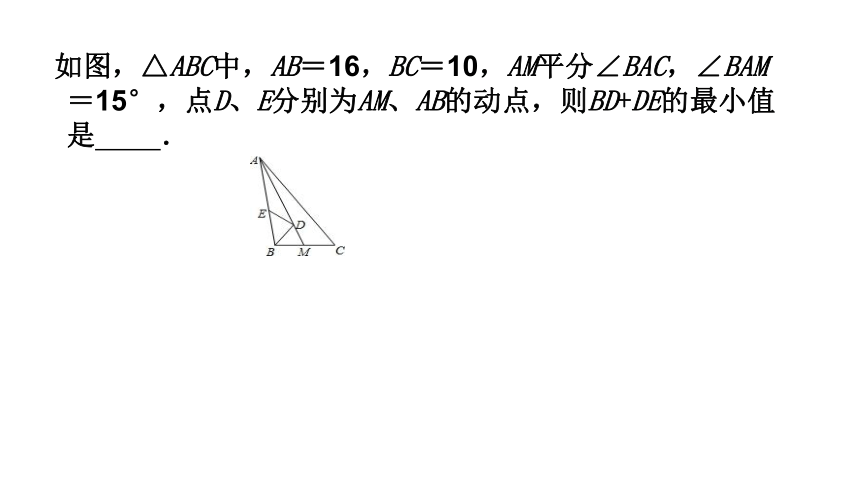
如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是 .
一 目标复习:连接直线外一点与直线上各点的线中,垂线段最短两点的所有连线中,线段最短;
。
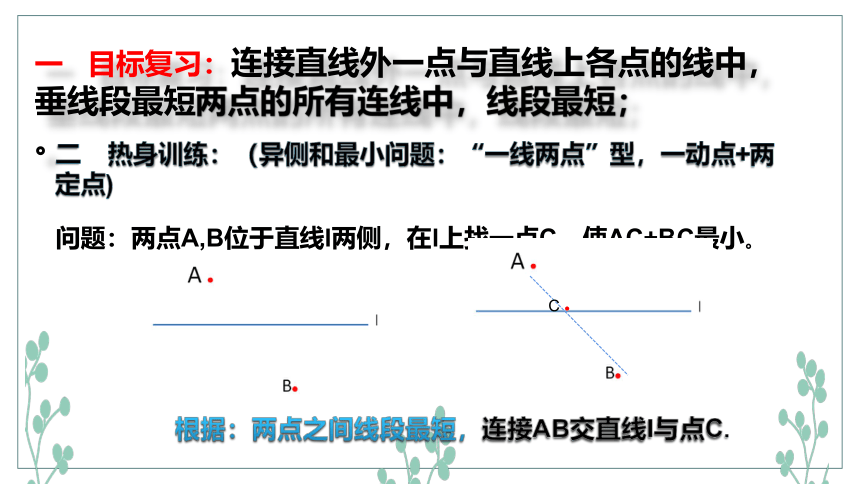
二 热身训练:(异侧和最小问题:“一线两点”型,一动点+两定点)
问题:两点A,B位于直线l两侧,在l上找一点C,使AC+BC最小。
根据:两点之间线段最短,连接AB交直线l与点C.
C ●
.
B
A
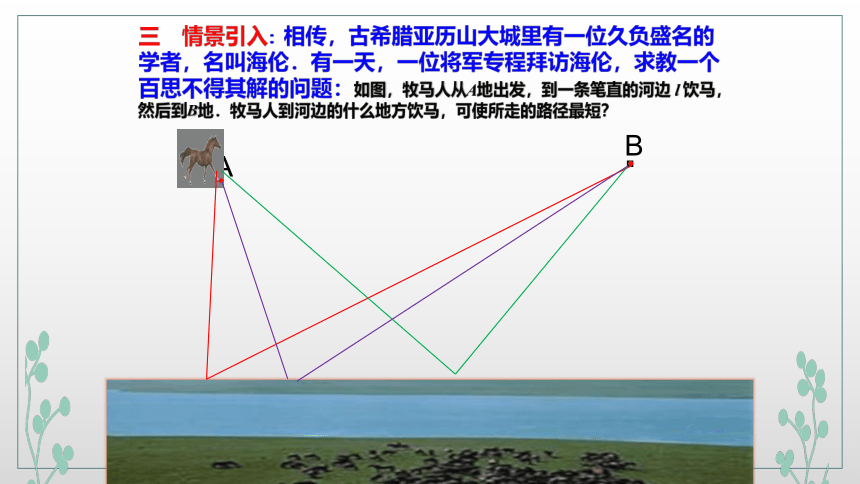
三 情景引入:相传,古希腊亚历山大城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:如图,牧马人从A地出发,到一条笔直的河边 l 饮马,然后到B地.牧马人到河边的什么地方饮马,可使所走的路径最短?
●
●
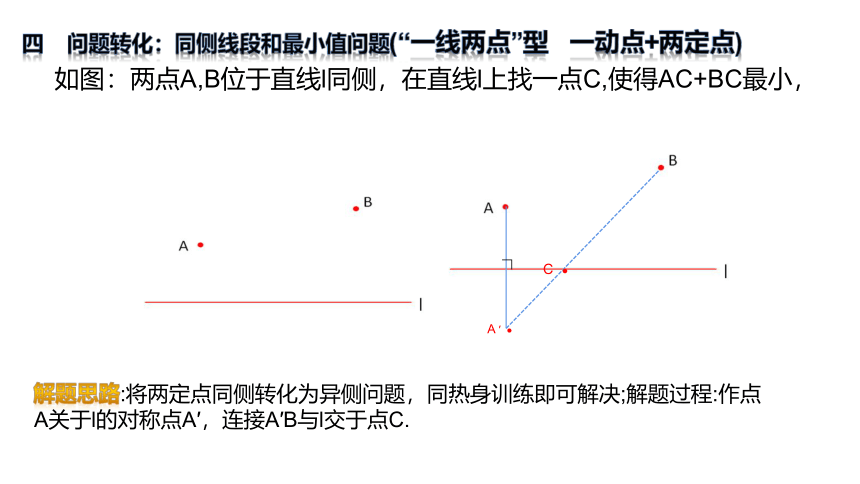
四 问题转化:同侧线段和最小值问题(“一线两点”型 一动点+两定点)
如图:两点A,B位于直线l同侧,在直线l上找一点C,使得AC+BC最小,
A ′ ●
解题思路:将两定点同侧转化为异侧问题,同热身训练即可解决;解题过程:作点A关于l的对称点A′,连接A′B与l交于点C.
C ●
∟
思考:如何验证AC+BC最短?
分析:为证明C的位置即为所求,可在直线外任取一点C ′,如图连接,证明AC+BC ﹤AC ′+BC ′。
你有什么收获?你能用一句话概括这个模型吗
五 及时训练:
1.E、F是△ABC的边AB、AC上的点,你能在BC上确定一点P是使△PEF的周长最短吗?
●
●
E′
P
∟
及时训练:
2.如图,在Rt △ABC中,AC=BC,点D是AB的中点,E是AC上任意一点,在CD上找一点P使PA+PE最小。
●
P
如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
如图,等边△ABC中,BD⊥AC于D,AD=3.5cm.点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE 最短,则PE+QE的最小值为 cm.
六 能力测试: (“一点两线型”,两动点+一定点)
1.点P是∠AOB内部一点,在OA上找一点M,在OB上找一点N, 使得△PMN周长最小。
P′
P′′
●
●
M
N
∟
∟
7.如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 .
1如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )
2如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
3.如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=40°,则∠AOB=( )
能力测试(“两点两线”型,两动点+两定点)
2.如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.(课本练习P93第15题)
P ●
● Q
A ′
B ′
最短路径(将军饮马)问题
13.4 课题学习
教学内容分析:
最短路径问题在现实生活中经常遇到,初中阶段主要以“两点之间线段最短”“连接直线外一点与直线上各点的所有线段中,垂线段最短”为基础知识进行研究,本节以“牧马人饮马” 问题为载体开展对“最短路径”的课题研究让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”。
教学目标:
能利用轴对称解决简单的最短路径问题,在探究的过中体会轴对称的桥梁作用,感悟转化的数学思想。
如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
想想这个题用了什么原理求线段的最短
如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是 .
一 目标复习:连接直线外一点与直线上各点的线中,垂线段最短两点的所有连线中,线段最短;
。
二 热身训练:(异侧和最小问题:“一线两点”型,一动点+两定点)
问题:两点A,B位于直线l两侧,在l上找一点C,使AC+BC最小。
根据:两点之间线段最短,连接AB交直线l与点C.
C ●
.
B
A
三 情景引入:相传,古希腊亚历山大城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:如图,牧马人从A地出发,到一条笔直的河边 l 饮马,然后到B地.牧马人到河边的什么地方饮马,可使所走的路径最短?
●
●
四 问题转化:同侧线段和最小值问题(“一线两点”型 一动点+两定点)
如图:两点A,B位于直线l同侧,在直线l上找一点C,使得AC+BC最小,
A ′ ●
解题思路:将两定点同侧转化为异侧问题,同热身训练即可解决;解题过程:作点A关于l的对称点A′,连接A′B与l交于点C.
C ●
∟
思考:如何验证AC+BC最短?
分析:为证明C的位置即为所求,可在直线外任取一点C ′,如图连接,证明AC+BC ﹤AC ′+BC ′。
你有什么收获?你能用一句话概括这个模型吗
五 及时训练:
1.E、F是△ABC的边AB、AC上的点,你能在BC上确定一点P是使△PEF的周长最短吗?
●
●
E′
P
∟
及时训练:
2.如图,在Rt △ABC中,AC=BC,点D是AB的中点,E是AC上任意一点,在CD上找一点P使PA+PE最小。
●
P
如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
如图,等边△ABC中,BD⊥AC于D,AD=3.5cm.点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE 最短,则PE+QE的最小值为 cm.
六 能力测试: (“一点两线型”,两动点+一定点)
1.点P是∠AOB内部一点,在OA上找一点M,在OB上找一点N, 使得△PMN周长最小。
P′
P′′
●
●
M
N
∟
∟
7.如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 .
1如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )
2如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
3.如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=40°,则∠AOB=( )
能力测试(“两点两线”型,两动点+两定点)
2.如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.(课本练习P93第15题)
P ●
● Q
A ′
B ′
